|
|
| (98 intermediate revisions by the same user not shown) |
| Line 3: |
Line 3: |
| | =Conclusions= | | =Conclusions= |
| | | | |
| − | #A 0.3 (0.6) Tesla Solenoid with a diameter to allow a 9.74 (3.94) cm diameter pipe would collect a positron per thousand incident electrons on a 2mm thick PbBi target with 0.125 mm thick SS windows. | + | #A 0.3 (0.6) Tesla Solenoid with a diameter to allow a 9.74 (3.94) cm diameter pipe would collect a positron per thousand incident electrons on a 2mm thick LBE target with 0.25 mm thick SS windows. |
| | + | # A 15 cm long, 0.2 Tesla solenoid with a 3.94 diameter beam pipe would collect a positron per two thousand electrons impinging a 2mm thick LBE target with 0.25 mm thick SS windows. |
| | #A 4 Tesla Solenoid will remove beam pipe heating from scattered electrons downstream of the target when using a 3.94 cm diameter beam pipe. | | #A 4 Tesla Solenoid will remove beam pipe heating from scattered electrons downstream of the target when using a 3.94 cm diameter beam pipe. |
| | | | |
| − | =Task List= | + | =Reports= |
| | | | |
| − | 1.) Report on previous simulation work. Target thickness optimization, beam heating, and positron rate as a function of beam pipe radius, mention that event files are now available. Deliver by Nov. 30. 3-5 pages.
| + | [[Niowave_Report_11-30-2015]] |
| | | | |
| − | 2.) Create a positron (10,000 positrons) and electron event file containing t,x,y,z,Px,Py,Pz for positrons exiting the solenoid and an incident Gaussian beam 1cm in diameter and with a sigma of 1cm.
| |
| | | | |
| − | 3.) Determine the back ground when using a 3.94 diameter beam pipe and Solenoid fields of 0.3 and 0.6 Tesla for a NaI detector placed at
| + | deadline 4/12/16 |
| | | | |
| − | =Beam Pipe Heating=
| |
| | | | |
| | + | ==[[Niowave_9-2015]]== |
| | + | ==[[Niowave_10-2015]]== |
| | + | ==[[Niowave_11-2015]]== |
| | + | ==[[Niowave_12-2015]]== |
| | + | ==[[Niowave_1-2016]]== |
| | + | ==[[Niowave_2-2016]]== |
| | + | ==[[Niowave_3-2016]]== |
| | + | ==[[Niowave_4-2016]]== |
| | + | ==[[Niowave_5-2016]]== |
| | + | ==[[Niowave_6-2016]]== |
| | | | |
| − | A 10 MeV electron beam with a radius of 0.5 cm was incident on a 2 mm thick PbBi target. The target is positioned at Z = -902 mm.
| + | =Task List= |
| − | | |
| − | | |
| − | [[File:TF_Niowave_SolenoidDesign_9-3-15.png | 200 px]] [[File:TF_Niowave_SolenoidDesign_9-11-15.png | 200 px]]
| |
| − | | |
| − | | |
| − |
| |
| − | {| border="1"
| |
| − | |Element || dimension
| |
| − | |-
| |
| − | | Inner beam pipe radius || 1.74 cm
| |
| − | |-
| |
| − | | Inner beam pipe thickness || 0.165 cm
| |
| − | |-
| |
| − | |water jacket thickness || 0.457 cm
| |
| − | |-
| |
| − | | outer beam pipe radius || 2.362 cm
| |
| − | |-
| |
| − | | outer beam pipe thickness || 0.165 cm
| |
| − | |-
| |
| − | | Solenoid inner radius || 2.527 cm
| |
| − | |-
| |
| − | | Solenoid outer radius || 4.406 cm
| |
| − | |}
| |
| | | | |
| | + | 0.) 34.8 mm pipe, 0.0 -> 0.5 Tesla, E= 6,8,10 MeV. |
| | | | |
| − | ==Max available power from beam heating==
| |
| | | | |
| − | If you assume a 1mA beam then the beam power incident on the target is
| + | 1.) Create a positron (10,000 positrons) and electron event file containing t,x,y,z,Px,Py,Pz for positrons exiting the solenoid and an incident Gaussian beam 1cm in diameter and with a sigma of 1cm. |
| | | | |
| − | Beam Power = E(MeV) <math> \cdot </math>I (<math>\mu</math> A) = 10 MeV <math>\times</math> 1000 mA = 10 kW
| + | compare distributions with and without solenoid. |
| | | | |
| − | If the beam does not interact with the target and all the beam power is distributed uniformly along a 100 cm long beam pipe with a diameter of 3.38 cm then the power deposited per area would be
| + | 2.) Determine the back ground when using a 3.48 diameter beam pipe and Solenoid field of 0.2 for a NaI detector placed at |
| | | | |
| − | :<math>10000 \mbox{W} \times \frac{1}{100 \mbox{cm}}\times \frac{1}{ \pi \times 3.48 \mbox {cm} } = 2.3 \frac{\mbox{W}}{\mbox{cm}^2}</math>
| + | 3.) Experiment, install dipole and solenoid in the tunnel. |
| | | | |
| | + | =Beam Pipe Heating= |
| | | | |
| − | A simulation predicts that about 8 out of 20 electrons will interact with the target and intercept a 34.8 mm diameter beam pipe surrounding the target.
| + | [[PbBi_BeamPipeHeatin_2015]] |
| − | | |
| − | ==Heating along the Z-axis==
| |
| − | | |
| − | GEANT4 predicts that scattered electrons, photons, and positrons (mostly scattered electrons) deposit
| |
| − | | |
| − |
| |
| − | {| border="1"
| |
| − | | [[File:BeamPipeDepEmev_34.8_082915.png |200px]] || [[File:MCNPXBeamPipeDepEmev_34.8_090315.png |200px]]
| |
| − | |+ Energy deposited (MeV) in a 1 m long 3.48 cm diameter beam pipe surrounding a 2 mm target located at Z=-900 mm.
| |
| − | |}
| |
| − | | |
| − | According to the above figure, GEANT4 predicts a total of <math>3.08\times 10^7</math> MeV (the integral adds up the energy in each 1cm bin) of energy will be deposited in
| |
| − | a 1m long beam pipe surrounding a 2 mm thick PbBi target located at Z=-902 mm when 20 million electrons impinge the target. The peak energy deposition is 0.3 MeV/e<math>^-</math>
| |
| − | | |
| − | If this energy were uniformly distributed along the 5 mm thick beam pipe having a diameter of 3.48 cm then I would see
| |
| − | | |
| − | :<math>3.08 \times 10^{10} \mbox{keV} \times \frac{1}{100 \mbox{cm}}\times \frac{1}{ \pi \times 3.48 \mbox {cm} } \times \frac{1}{2 \times 10^7 \mbox{e}^-}=3.5\frac{\mbox{keV}}{\mbox{cm}^2 \;\;\mbox{e}^-}</math>
| |
| − | | |
| − | | |
| − | | |
| − | if you assume a 1 mA beam of electrons then this becomes
| |
| − | | |
| − | <math>\left ( \frac{3.5 \; \mbox{W} }{ \mbox{cm}^2 } \right) </math>
| |
| − | | |
| − | I converted the above histogram to deposited power by 1000 mA, divide by the number of incident electrons, divide by the circumference of the beam pipe, convert the number of electrons to Coulombs, and use a unit conversion from MeV to W-s per MeV.
| |
| − | | |
| − | <math>\left(Counts \frac{\mbox{MeV}}{\mbox{cm}}\right) \times \left( \frac{1}{2 \times 10^{7} \mbox{e}^-} \right ) \times \left( \frac{1}{ \pi \times 3.48 \mbox{cm}} \right ) \times \left( \frac{1. \times 10^{-3}\mbox{ C}}{\mbox{s} }\right )\times \left( \frac{\mbox{e}^- }{1.6 \times 10^{-19}\mbox{ C}}\right ) \left( \frac{1.6 \times 10^{-13}\mbox{W} \cdot \mbox{ s}}{\mbox{MeV} }\right ) \times </math>
| |
| − | | |
| − | If you use the above factors to weight the histogram, then the figure below shows that GEANT4 predicts a power deposition density of <math>= 4 \frac{W}{cm^2}</math>, 1 cm downstream of the target.
| |
| − | Back scattered electrons appear to create the hottest spot of <math>= 15 \frac{W}{cm^2}</math> about 1cm upstream of the target.
| |
| − |
| |
| − | {| border="1"
| |
| − | | [[File:BeamPipeDepE_34.8mmA_082815.png| 200 px]] ||[[File:BeamPipeDepE_34.8mmB_082815.png| 200 px]]
| |
| − | |-
| |
| − | | Power Deposition Zoomed in and 902 mm offset applied ||Power deposition over the 1 m long beam pipe
| |
| − | |-
| |
| − | |}
| |
| − | | |
| − | | |
| − | | |
| − | | |
| − | The plot below shows the energy deposited in MeV along the pipe. The Z axis is along the beam direction. The distance around the beam pipe is determine by taking the pipe radius (34.8 mm) and multiplying it by the Phi angle around the pipe. The bins are 1cm x 1cm.
| |
| − | | |
| − | | |
| − | | |
| − |
| |
| − | {| border="1"
| |
| − | | [[File:BeamPipeDepEPhi_34.8_082815.png |200px]] ||[[File:BeamPipeDepE_34.8_082815.png| 200 px]]
| |
| − | |+ A maximum of 450,000 MeV is deposited in a 1 cm<math>^2</math> bin when 20 Million , 10 MeV electrons are incident on a 2 mm thick PbBi target located at Z=-902 mm.
| |
| − | |}
| |
| − | | |
| − | Below is energy deposited contributions from from photons(AVSzWg), positrons (AVSzWpos), and electrons.
| |
| − | | |
| − | | |
| − | [[File:BeamPipeDepE_34.8_082815_parttype.png | 200 px]]
| |
| − | | |
| − | Why is the positron hotspot upstream of the target?
| |
| − | | |
| − | | |
| − | | |
| − | | |
| − | | |
| − | root commands used
| |
| − | | |
| − | TH2D *AVSz=new TH2D("AVSz","AVSz",100,-1000,0,12,-60,60)
| |
| − | BeamPipeE->Draw("35.*atan(PosYmm/PosXmm):PosZmm>>AVSz","DepEmeV");
| |
| − | AVSz->Draw("colz");
| |
| − | | |
| − | | |
| − | | |
| − | [[BeamPipeHeating_4mmthick_PbBi_PositronTarget]]
| |
| − | | |
| − | ==Scattered Electron Momentum and Energy lot in Beam Pipe==
| |
| − | | |
| − | [[File:ScatElectronMom_34.8_090415.png | 200 px]]
| |
| − | [[File:ElectronEdeposited_34.8_090415.png | 200 px]]
| |
| − | | |
| − | ==Unit conversion==
| |
| − | | |
| − | The energy deposited by photon, electrons, and positrons is predicted by GEANT4 and recorded in energy units of keV per incident electron on the PbBi target. To convert this deposited energy to a power you need to assume a beam current. Assuming 1 beam current of 1 mA, the conversion is given easily as
| |
| − | | |
| − | <math>\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) \times \left( \frac{ \mbox{e}^-}{1.6 \times 10^{-19}\mbox{C}} \right ) \times \left( \frac{1 \times 10^{-3} \mbox{C}}{\mbox{s}} \right ) \times \left( \frac{1.6 \times 10^{-16}\mbox{W} \cdot \mbox{ s}}{\mbox{keV} }\right )</math>
| |
| − | | |
| − | <math>\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) = \left( \frac{\mbox{W} }{\mbox{cm}^2 } \right )</math>
| |
| − | | |
| − | ==Results Table==
| |
| − | | |
| − |
| |
| − | {| border="1"
| |
| − | {| border="1"
| |
| − | | Beam Pipe Diameter (mm) || Hot Spot (<math>MeV/e^-</math>)|| Hot Spot (<math>keV/cm^2/e^-</math>)
| |
| − | |-
| |
| − | | 34.8 || 0.35
| |
| − | |-
| |
| − | | 47.5 || 0.24
| |
| − | |-
| |
| − | | 60.2 || 0.20
| |
| − | |-
| |
| − | | 72.9 || 0.16
| |
| − | |-
| |
| − | | 97.4 || 0.12
| |
| − | |-
| |
| − | |}
| |
| | | | |
| | =Converter target properties= | | =Converter target properties= |
| | | | |
| − | Definition of Lead Bismuth
| |
| | | | |
| | + | [[PbBi_NioWave_TargetProperties_2015]] |
| | | | |
| − | 1cm diameter target
| |
| − | 2 mm thick PbBi
| |
| | | | |
| − | 0.5 Tesla solenoid
| + | =Target thickness optimization= |
| | | | |
| | + | ==[[PbBi_THickness_CylinderBeam]]== |
| | | | |
| − | Desire to know
| + | ==[[PbBi_THickness_GaussBeam]]== |
| | | | |
| − | Emmittance (mrad * mm)
| + | == [[PbBi_THickness_PntSource]]== |
| | | | |
| − | dispersion (Delta P/P) (mradian/1000th mm/1000th)
| + | =Solenoid= |
| | | | |
| − | of electrons after the PbBi target.
| + | ==Uniform ideal Solenoid== |
| | | | |
| | + | === [[PbBi_BeamPipeHeating_w_Solenoid_2015]]=== |
| | | | |
| − | pole face rotation in vertical plane.
| + | ===[[PbBi_60cmLong_Solenoid_Collection_Efficiency_2015]]=== |
| | | | |
| − | =G4BeamLine and MCNPX= | + | ==Positron & Electron event files== |
| | | | |
| − |
| + | [[PbBi_PosEventFiles_VaccumGaps_2015]] |
| − | ==Target thickness optimization==
| |
| | | | |
| − | ===[[PbBi_THickness_GaussBeam]]===
| + | [[PbBi_PosEventFiles_NoGaps_2016]] |
| − | Dmitry's processing of Tony's GEANT simulations showing transverse phase space portrait (left) and longitudinal phase space portrait (right). Phase space portraits show coordinate x or y vs
| |
| − | diveregense=px/pz or py/pz (or time vs kinetic energy ). Captions show:
| |
| | | | |
| − | 1. geometric (not normalized) emittance for transverse and emittance for longitudinal phase space portraits (ellipse areas divided by "pi")
| + | ==Solenoid Map== |
| | | | |
| − | 2. Twiss parameters
| + | Inner Radiusu= |
| | | | |
| − | 3. Ellipse centroid for longitudinal phase portrait
| + | Outer Radius = |
| | | | |
| − | 4. sqrt(beta*emittance) and sqrt(gamma*emittance) - half sizes of the projections of the ellipses on the coordinate and divergence axes respectively.
| + | Length = |
| | | | |
| − | Electrons - RMS
| + | Current= |
| | | | |
| − | [[File:Ed1.png| 400 px]]
| + | Magnetic Field Map in cylindrical coordinates (Z & R) from Niowave |
| | | | |
| − | Electrons - 68.2% core
| + | =Rear Window Thickness= |
| | | | |
| − | [[File:Ed2.png| 400 px]]
| |
| | | | |
| − | Positrons - RMS
| + | Question: Will a thicker downstream exit window increase the positron production efficiency by providing more material for a brehm photon to pair produce in? |
| | | | |
| − | [[File:Pd1.png| 400 px]]
| |
| | | | |
| − | Positrons - 68.2% core | + | Positrons were counted exiting a ideal 0.2 Tesla solenoid that was 15 cm long. A ten MeV electron beam with a 0.5 cm cylindrical radius impinged a 2mm thick PbBi liquid target that had a surface area of 2.54 cm x 2.54 cm. A 0.25 mm thick stainless steel entrance window was used. |
| − | | |
| − | [[File:Pd2.png| 400 px]]
| |
| − | | |
| − | === [[PbBi_THickness_CylinderBeam]]===
| |
| − | Dmitry's processing of Tony's GEANT simulations showing transverse phase space portrait (left) and longitudinal phase space portrait (right). Phase space portraits show coordinate x or y vs
| |
| − | diveregense=px/pz or py/pz (or time vs kinetic energy ). Captions show:
| |
| − | | |
| − | 1. geometric (not normalized) emittance for transverse and emittance for longitudinal phase space portraits (ellipse areas divided by "pi")
| |
| − | | |
| − | 2. Twiss parameters
| |
| − | | |
| − | 3. Ellipse centroid for longitudinal phase portrait
| |
| − | | |
| − | 4. sqrt(beta*emittance) and sqrt(gamma*emittance) - half sizes of the projections of the ellipses on the coordinate and divergence axes respectively.
| |
| − | | |
| − | Electrons - RMS
| |
| − | | |
| − | [[File:E1.png| 400 px]]
| |
| − | | |
| − | Electrons - 68.2% core
| |
| − | | |
| − | [[File:E2.png| 400 px]]
| |
| − | | |
| − | Positrons - RMS
| |
| − | | |
| − | [[File:P1.png| 400 px]]
| |
| − | | |
| − | Positrons - 68.2% core
| |
| − | | |
| − | [[File:P2.png| 400 px]]
| |
| − | | |
| − | === [[PbBi_THickness_PntSource]]===
| |
| − | | |
| − | Electrons and Positrons after 2mm of LBE:
| |
| − | | |
| − | Electrons:
| |
| − | | |
| − | [[File:e01.png| 200 px]][[File:e02.png| 200 px]]
| |
| − | | |
| − | Positrons:
| |
| − | | |
| − | [[File:p01.png| 200 px]][[File:p02.png| 200 px]]
| |
| − | | |
| − | ===Energy Deposition in Target system (Heat)===
| |
| − | | |
| − | | |
| − | [[File:ElectronTracks.png| 200 px]][[File:PhotonTracks.png| 200 px]]
| |
| − | | |
| − | [[File:ElectronEnergy.png| 200 px]][[File:PhotonEnergy.png| 200 px]]
| |
| − | | |
| − | MCNPX simulations of energy deposition into different cells are below. There is a slight overestimate (they add up to about 120%). Positrons contribute less than 1% of electrons' contribution. No magnetic filed is assumed.
| |
| − | | |
| − | [[File:Model.png| 400 px]]
| |
| − | | |
| − | [[File:Tablen1.png| 200 px]]
| |
| − | | |
| − | [[File:Tablen2.png| 200 px]]
| |
| − | | |
| − | ==Solenoid==
| |
| − | | |
| − | ===Uniform ideal Solenoid===
| |
| − | | |
| − | ==== Beam Pipe Heating with SOlenoid====
| |
| − | | |
| − | The energy deposited by electrons scattered into a 3.48 diameter stainless steel beam pipe (1.65 mm thick) from a PbBi target as a function of a uniform Solenoidal magnetic field.
| |
| − | | |
| − | The histogram is binned in 100 (10 cm) bin widths. The surface area becomes <math>10 cm \times 2 \pi 3.48/2 = 109.33 cm^2</math>
| |
| − | | |
| − | | |
| − | To convert From Mev/ e- to kW/cm^2 assuming a current of 1mA (10^-3 C/s) you
| |
| − | | |
| − | <math>\left( \frac{\mbox{MeV}}{\mbox{cm}^2 \mbox{e}^-}\right) \times \left( \frac{ \mbox{e}^-}{1.6 \times 10^{-19}\mbox{C}} \right ) \times \left( \frac{1 \times 10^{-3} \mbox{C}}{\mbox{s}} \right ) \times \left( \frac{1.6 \times 10^{-13}\mbox{W} \cdot \mbox{ s}}{\mbox{MeV} }\right )</math>
| |
| − | | |
| − | <math>\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) = \left( \frac{\mbox{W} }{\mbox{cm}^2 } \right )</math>
| |
| − | | |
| − | | |
| − |
| |
| − | {| border="1"
| |
| − | {| border="1"
| |
| − | | B-field (Tesla) || Hot Spot (<math>MeV/e^-</math>)
| |
| − | |-
| |
| − | | 0.0 || 0.35
| |
| − | |-
| |
| − | | 0.3 || 0.35
| |
| − | |-
| |
| − | | 1.0 || 0.35
| |
| − | |-
| |
| − | | 1.5 || 0.22
| |
| − | |-
| |
| − | | 2.0 || 0.10
| |
| − | |-
| |
| − | | 4.0 || 0.002
| |
| − | |+
| |
| − | |}
| |
| − | | |
| − |
| |
| − | {| border="1"
| |
| − | | [[File:BeamPipeDepEmev-vs-B.png |200px]] || [[File:BeamPipeDepPower-vs-B.png |200px]]
| |
| − | |+ Energy deposited (MeV) along a 1 m long beam pipe of stainless steel 1.65 mm thick.
| |
| − | |}
| |
| − | | |
| − | With SS windows
| |
| − | Positrons->Draw("sqrt(evt.BeamPosPosX*evt.BeamPosPosX+evt.BeamPosPosY*evt.BeamPosPosY)","evt.BeamPosMomZ>0 && evt.BeamPosPosZ>-500 && sqrt(evt.BeamPosPosX*evt.BeamPosPosX+evt.BeamPosPosY*evt.BeamPosPosY)<97.4/2"); | |
| − | | |
| − | ====Positron Collection rates with Solenoid====
| |
| − |
| |
| − | {| border="1"
| |
| − | | [[File:PositronEventWithSolenoid_09-16-15A.png|200px]] ||[[File:PositronEventWith0.3Solenoid_09-16-15A.png|200px]]
| |
| − | |-
| |
| − | | When the solenoid is 1.5 Tesla, a 10 MeV electron produces a 6.5 MeV photon that pair produces a 4.4 MeV positron and a 1 MeV electron || Same Event but this time the solenoid is 0.3 Tesla and the positron hits the beam pipe, annihilates and makes two 511 keV photons
| |
| − | |+ Sample Positron Production Events
| |
| − | |}
| |
| − |
| |
| − | {| border="1"
| |
| − | | [[File:PositronEventWithSolenoid_09-16-15B.png|200px]] ||[[File:PositronEventWith0.3Solenoid_09-16-15B.png|200px]]
| |
| − | |-
| |
| − | | When the solenoid is set to 1.5 Tesla, a 10 MeV electron produces three photons less than 1 MeV in the target, two of them compton scatter in the beam pipe || The same event but this time the electron produces only 1 photon than ionizes in the target
| |
| − | |+ Sample Brem event producing no positrons
| |
| − | |}
| |
| − | | |
| − | | |
| − | With SS windows
| |
| − | Positrons->Draw("sqrt(evt.BeamPosPosX*evt.BeamPosPosX+evt.BeamPosPosY*evt.BeamPosPosY)","evt.BeamPosMomZ>0 && evt.BeamPosPosZ>-500 && sqrt(evt.BeamPosPosX*evt.BeamPosPosX+evt.BeamPosPosY*evt.BeamPosPosY)<97.4/2");
| |
| | | | |
| | + | Target is at -106 mm, entrance SS window is at -108.25 mm , exit SS window is at -103.75 mm, A sensitive detector for positron is placed at Z= +44mm. The sensitive detector is a cylinder of radius 11.74 cm. |
| | | | |
| | {| border="1" | | {| border="1" |
| | {| border="1" | | {| border="1" |
| − | | B-field (Tesla) || || 39.4 mm diameter pipe || 47.5 || 60.2 || 72.9 || 97.4 | + | | SS Exit WIndow Thickness (mm) || Positrons/Million electrons |
| − | |-
| |
| − | | 0.0 || 0.35 || 1,2,4,4,5 || 2,3,4,4,6 || 4,4,6,7,9 || 6,8,9,10,11 || 16,14,15,16,17
| |
| | |- | | |- |
| − | | 0.1 || ||225,236,250,246,249=241<math> \pm</math> 10 || 282,282,293,294,306=291<math> \pm</math> 10 || 373,366,370,364,373=369<math> \pm</math> 4 || 451,437,440,438,451=443<math> \pm</math> 7 || 602,584,563,558,570=575<math> \pm</math> 18 | + | |0.0 || 1142,1096,1149,1073,1083 = 1109 +/- 35 |
| − | |-
| |
| − | | 0.3 || 0.35 || 626,619,596,619,611 =614<math> \pm</math> 11|| 720,726,706,730,717=720<math> \pm</math> 9|| 871,864,840,841,834 =850<math> \pm</math> 16|| 987,968,939,943,952 =958<math> \pm</math> 20|| 1118,1106,1069,1067,1080=1088<math> \pm</math> 23
| |
| | |- | | |- |
| − | | 0.6 || ||929,935,949,969,961=949<math> \pm</math> 17 ||1022,1031,1046,1059,1052 =1042<math> \pm</math> 15 || 1120,1130,1152,1154,1146 =1140<math> \pm</math> 15|| 1168,1184,1210,1221,1206 =1198<math> \pm</math> 21|| 1212, 1218,1240,1254,1242=1233<math> \pm</math> 18 | + | | 0.25 || 774,836,800,785,798 = 798 +/- 23 |
| | |- | | |- |
| − | | 1.0 || 0.35 ||1117,1085,1083,1061,1085=1086<math> \pm</math> 20 || 1188,1154,1140,1111,1134=1145<math> \pm</math> 28||1225,1190,1178,1149,1172 =1183<math> \pm</math> 28||1243.1208,1195,1164,1184=1199<math> \pm</math> 30|| 1252,1219,1206,1178,1200=1211<math> \pm</math> 27 | + | | 0.5 || 693,704,713,697,715 = 704 +/- 10 |
| | |- | | |- |
| − | | 1.5 || 0.22 || | + | | 1.0 || 587,606,548,592,550 =577 +/- 26 |
| − | |-
| |
| − | | 2.0 || 0.10 ||1198,1210,1215,1223,1176=1204<math> \pm</math> 18 || 1216,1227,1235,1241,1196 =1223<math> \pm</math> 18|| 1237,1243,1252,1257,1214=1241<math> \pm</math> 17|| 1249,1252,1262,1266,1225 =1251<math> \pm</math> 16|| 1257,1262,1270,1276,1234=1260<math> \pm</math> 16
| |
| − | |-
| |
| − | | 4.0 || 0.002 ||
| |
| | |+ | | |+ |
| | |} | | |} |
| | | | |
| | | | |
| − |
| + | ;Conclusion 1: Positron production efficiency improves when the exit window is made thinner |
| − | {| border="1"
| |
| − | | [[File:PositronRates-vs-SolenoidField_10-1-15.png |200px]]
| |
| − | |+ Positron Rates -vs- Solenoid Field for 2mm thick PbBi target and several Beam pipe diameters
| |
| − | |}
| |
| | | | |
| − | ===Positron & Electron event files===
| + | ;Conclusion 2 : You loose about 28 +/- 4 % of the positrons in the 0.25 mm thick SS exit window. |
| | | | |
| − | Event files were generated assuming an ideal solenoid having an inner radius of 2.527 cm surrounding a beam pipe with a radius of 1.74 cm. Electrons impinge a 2mm thick PbBi liquid target that has a surface area of 2.54 cm x 2.54 cm. Stainless steel windows 0.25 mm thick sandwhich the PbBi target at locations Z= -90.325 and Z= -89.875 cm. The target is located at Z =-90.1 cm and the beam begins 20 cm upstream at Z = -110.1 cm. The incident electron beam is a 0.5 cm radius cylinder.
| + | =Background studies= |
| | | | |
| | + | ==Brem Spectrum== |
| | | | |
| − | /vis/viewer/zoom 2
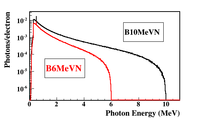
| + | Below is the photon energy distribution (from Brem & pair production) using a 2mm Pb target for two different incident electron energies; 6 and 10 MeV. The photons are 1 cm downstream of the target and intersection a large forward region. |
| | | | |
| − | /gps/pos/centre 0.0 0.0 -150.
| + | [[File:PbBi_Brem_6-10MeV_4-7-16.png | 200 px]] |
| | | | |
| − | /vis/viewer/panTo -90.1 0 cm
| + | insert photon spacial distributions |
| | | | |
| − | /vis/viewer/reset
| + | Now move the scoring region downstream to a position representing the location of a NaI detector. |
| − | | |
| − | ===Solenoid Map===
| |
| − | | |
| − | Inner Radiusu=
| |
| − | | |
| − | Outer Radius =
| |
| − | | |
| − | Length =
| |
| − | | |
| − | Current=
| |
| − | | |
| − | Magnetic Field Map in cylindrical coordinates (Z & R) from Niowave
| |
| | | | |
| | =Beam Line Design= | | =Beam Line Design= |