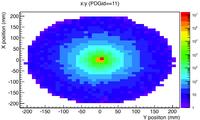
PbBi THickness GaussBeam
Use Gaussian to make a incident uniform beam that is 1 cm in diameter and has a beam sigma of 1 cm , then cut out the beam to have a 0.5 cm circular radius.
First simple test is to send 1 million, 10 MeV electrons towards a PbBi target and count how many positrons leave the downstream side
The Random number seed is set by Time in G4beamline to use a different set of pseudo random numbers each time it is run
The G4Beamlin incident electron beam has the following properties
beam gaussian particle=e- nEvents=1000000 beamZ=0.0
sigmaX=1.0 sigmaY=1.0 sigmaXp=0.100 sigmaYp=0.100
meanMomentum=10.0 sigmaP=4.0 meanT=0.0 sigmaT=0.0
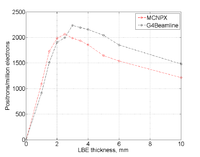
| PbBi Thickness (mm) | #positrons/million electrons (G4Beamline) | #positrons/million electrons (MCNPX) |
| 1 | 960,874, 916,934,897=916 +/- 33 | 1091 |
| 1.5 | 1508 | 1728 |
| 2 | 1963,1919,1880,1877,1970 = 1902 43 | 1984 |
| 2.5 | 1997 | 2062 |
| 3 | 2233,2250, 2251,2226 , 2222=2236 13 | 1986 |
| 3.5 | 2193 | 1938 |
| 4 | 2184,2156,2089,2173,2181=2157 39 | 1858 |
| 5 | 2042 | 1646 |
| 6 | 1851, 1932, 1857, 1896,1924 = 1892 37 | 1541 |
| 10 | 1480,1488 | 1216 |
Comparison of G4Beamline and MCNPX
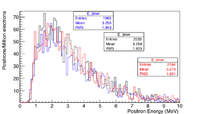
Energy Distribution
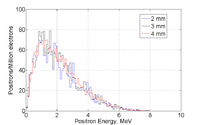
Angular distribution of positrons
I was unable to do anything other than a gaussian beam right now, I will try to do one later
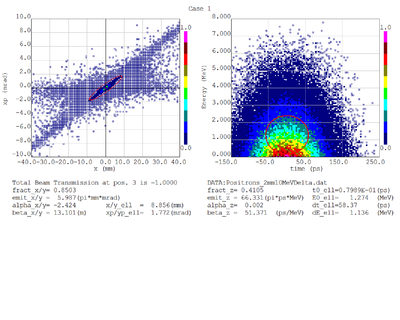
For now I have a gaussian with an 8mm RMS and 10 MeV incident electrons as shown below.
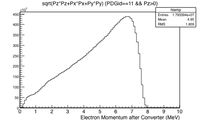
The positron and electron momentum distributions after the PbBi converter are shown below
A comma delimited text file with the above events in the format of
x,y,z,Px,Py,Pz
in units of cm for distance and MeV for momentum is located at
for positrons
http://www2.cose.isu.edu/~foretony/Positrons_2mm10MeV.dat
and
http://www2.cose.isu.edu/~foretony/Electrons_2mm10MeV.dat
for electrons
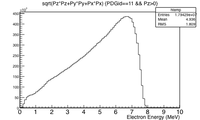
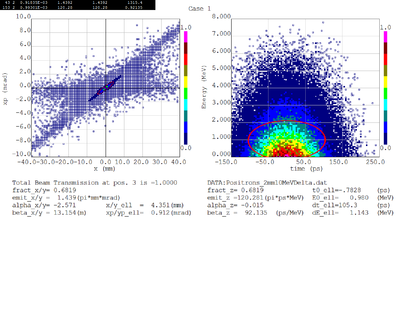
For now I have a gaussian with an 1mm RMS and 10 MeV incident electrons as shown below.
The positron and electron momentum distributions after the PbBi converter are shown below
A comma delimited text file with the above events in the format of
x,y,z,Px,Py,Pz
in units of cm for distance and MeV for momentum is located at
for positrons
http://www2.cose.isu.edu/~foretony/Positrons_2mm10MeVDelta.dat
and
http://www2.cose.isu.edu/~foretony/Electrons_2mm10MeVDelta.dat
for electrons
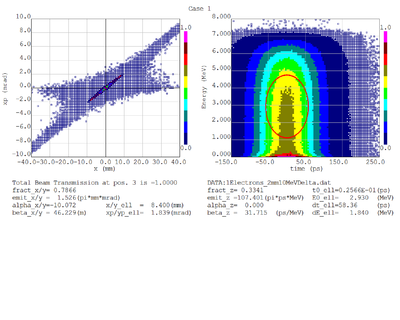
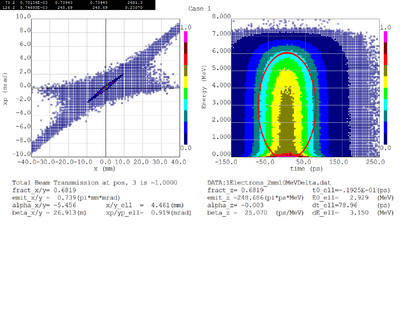
Dmitry's processing of Tony's GEANT simulations showing transverse phase space portrait (left) and longitudinal phase space portrait (right). Phase space portraits show coordinate x or y vs
diveregense=px/pz or py/pz (or time vs kinetic energy ). Captions show:
1. geometric (not normalized) emittance for transverse and emittance for longitudinal phase space portraits (ellipse areas divided by "pi")
2. Twiss parameters
3. Ellipse centroid for longitudinal phase portrait
4. sqrt(beta*emittance) and sqrt(gamma*emittance) - half sizes of the projections of the ellipses on the coordinate and divergence axes respectively.
Electrons - RMS
Electrons - 68.2% core
Positrons - RMS
Positrons - 68.2% core