Difference between revisions of "G4Beamline PbBi"

From New IAC Wiki
Jump to navigation Jump to search
 
(246 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
Development of a Positron source using a PbBi converter and a Solenoid
 
Development of a Positron source using a PbBi converter and a Solenoid
  
−
=Task List=
+
=Conclusions=
  
−
1.) new electron and positron files for the case of two 0.25 mm thick SS windows around the PbBi target.
+
#A 0.3 (0.6) Tesla Solenoid with a diameter to allow a 9.74 (3.94) cm diameter pipe would collect a positron per thousand incident electrons on a 2mm thick LBE target with 0.25 mm thick SS windows.
 +
# A 15 cm long, 0.2 Tesla solenoid with a 3.94 diameter beam pipe would collect a positron per two thousand electrons impinging a 2mm thick LBE target with 0.25 mm thick SS windows.
 +
#A 4 Tesla Solenoid will remove beam pipe heating from scattered electrons downstream of the target when using a 3.94 cm diameter beam pipe.
  
−
2.) Determine electron energy deposition in SS pipe per cm^2 of pipe surface area for pipes with a radius of 34.8, 47.5, 60.2, 72.9, and 97.4 mm and thickness of 5mm along the z-axis.
+
=Reports=
  
−
3.) Insert uniform B-field that can be scaled from 0 to 0.3 and 1 Telsa.
+
[[Niowave_Report_11-30-2015]]
  
−
=Beam Pipe Heating=
 
  
 +
deadline 4/12/16
  
−
A 10 MeV electron beam with a radius of 0.5 cm was incident on a 2 mm thick PbBi target.  The target is positioned at Z = -902 mm.  The plot below shows the energy deposited in MeV along the pipe.  The Z axis is along the beam direction.  The distance around the beam pipe is determine by taking the pipe radius (34.8 mm) and multiplying it by the Phi angle around the pipe.  The bins are 1cm x 1cm.
 
  
 +
==[[Niowave_9-2015]]==
 +
==[[Niowave_10-2015]]==
 +
==[[Niowave_11-2015]]==
 +
==[[Niowave_12-2015]]==
 +
==[[Niowave_1-2016]]==
 +
==[[Niowave_2-2016]]==
 +
==[[Niowave_3-2016]]==
 +
==[[Niowave_4-2016]]==
 +
==[[Niowave_5-2016]]==
 +
==[[Niowave_6-2016]]==
  
 +
=Task List=
  
−
+
0.) 34.8 mm pipe, 0.0 -> 0.5 Tesla, E= 6,8,10 MeV.
−
{| border="1"
 
−
| [[File:BeamPipeDepEPhi_34.8_082815.png |200px]] ||[[File:BeamPipeDepE_34.8_082815.png| 200 px]]
 
−
|+ About 450,000 MeV/cm^2 is deposited when 20 Million , 10 MeV electrons are incident on a 2 mm thick PbBi target located at Z=-902 mm.
 
−
|}
 
  
  
 +
1.)  Create a positron (10,000 positrons) and electron event file containing t,x,y,z,Px,Py,Pz  for positrons exiting the solenoid and an incident Gaussian beam 1cm in diameter and with a sigma of 1cm.
  
−
Beam Power = E(MeV) <math> \cdot </math>I (<math>\mu</math> A) = 10 MeV <math>\times</math> 1000 mA = 10 kW
+
compare distributions with and without solenoid.
  
−
If all of the beam power goes into a 150 cm long beam pipe with a radius of 3.38 cm then the power deposited per area would be
+
2.) Determine the back ground when using a 3.48 diameter beam pipe and Solenoid field of 0.2  for a NaI detector placed at
  
−
:<math>10000 \mbox{W}  \times \frac{1}{150 \mbox{cm}}\times \frac{1}{2 \pi \times 3.48 \mbox {cm} } = 3 \frac{\mbox{W}}{\mbox{cm}^2}</math>
+
3.) Experiment, install dipole and solenoid in the tunnel.
  
−
Projections onto the Z-axis
+
=Beam Pipe Heating=
  
 +
[[PbBi_BeamPipeHeatin_2015]]
  
−
+
=Converter target properties=
−
{| border="1"
 
−
| [[File:BeamPipeDepEmev_34.8_082915.png |200px]]
 
−
|+ Energy deposited (MeV) in a 1 m long 3.48 cm radius beam pipe surrounding a 2 mm target located at Z=-902 mm when 20 million electrons impinge the target.
 
−
|}
 
  
−
According to the above figure, GEANT4 predicts a total of <math>1.064 \times 10^7</math> MeV of energy will be deposited in
 
−
a 1m long beam pipe surrounding a 2 mm thick PbBi target located at Z=-902 mm when 20 million electrons impinge the target.
 
−
<math>\left( \frac{1.064 \times 10^7\mbox{MeV}}{2 \times 10^7 \mbox{e}^-}\right) = \frac{500\mbox{keV} }{\mbox{e}^- }</math>
 
  
−
If all of this energy were UNIFORMLY distriuted along the 3.48 cm radius pipe then the energy deposited per area would be
+
[[PbBi_NioWave_TargetProperties_2015]]
  
−
<math>\left(500\mbox{keV}}{100 \times 2 \pi \times 3.48 \mbox{cm}^2 \mbox{e}^-}\right)</math>
 
  
−
+
=Target thickness optimization=
−
{| border="1"
 
−
|+ GEANT4 predicts a power deposition density of <math>= 0.76 \frac{W}{cm^2}</math>, 3 cm downstream of the target. 
 
−
The total power density deposited on a 1 m long beam pipe is <math>= 24 \frac{W}{cm^2}</math>.  Back scattered electrons appear to creat the hottest spot of  <math>= 2.6 \frac{W}{cm^2}</math> about 3cm upstream of the target.
 
−
|-
 
−
| [[File:BeamPipeDepE_34.8mmA_082815.png| 200 px]] ||[[File:BeamPipeDepE_34.8mmB_082815.png| 200 px]]
 
−
|-
 
−
|}
 
  
−
I converted the above histogram to deposited power you would divide by the number of incident electrons, divide by the circumference of the beam pip, multiple the beam current, and use a unit conversion from MeV to W-s per MeV.
+
==[[PbBi_THickness_CylinderBeam]]==
  
−
<math>\left(Counts \frac{\mbox{MeV}}{\mbox{cm}}\right) \times \left( \frac{1}{2 \times 10^{7} \mbox{e}^-}  \right ) \times \left( \frac{1}{2 \times \pi \times 3.48 \mbox{cm}} \right )  \times  \left( \frac{1. \times 10^{-3}\mbox{ C}}{\mbox{s} }\right )\times \left( \frac{\mbox{e}^- }{1.6 \times 10^{-19}\mbox{ C}}\right ) \left( \frac{1.6 \times 10^{-13}\mbox{W} \cdot \mbox{ s}}{\mbox{MeV} }\right )  \times </math>
+
==[[PbBi_THickness_GaussBeam]]==
  
 +
== [[PbBi_THickness_PntSource]]==
  
 +
=Solenoid=
  
 +
==Uniform ideal Solenoid==
  
−
Below is energy deposited contributions from from photons(AVSzWg), positrons (AVSzWpos), and electrons.
+
=== [[PbBi_BeamPipeHeating_w_Solenoid_2015]]===
  
 +
===[[PbBi_60cmLong_Solenoid_Collection_Efficiency_2015]]===
  
−
[[File:BeamPipeDepE_34.8_082815_parttype.png | 200 px]]
+
==Positron & Electron event files==
  
−
Why is the positron hotspot upstream of the target?
+
[[PbBi_PosEventFiles_VaccumGaps_2015]]
  
 +
[[PbBi_PosEventFiles_NoGaps_2016]]
  
 +
==Solenoid Map==
  
 +
Inner Radiusu=
  
 +
Outer Radius =
  
−
root commands used
+
Length =
  
−
TH2D *AVSz=new TH2D("AVSz","AVSz",100,-1000,0,12,-60,60)
+
Current=  
−
BeamPipeE->Draw("35.*atan(PosYmm/PosXmm):PosZmm>>AVSz","DepEmeV");
 
−
AVSz->Draw("colz");
 
  
 +
Magnetic Field Map in cylindrical coordinates (Z & R) from Niowave
  
 +
=Rear Window Thickness=
  
−
[[BeamPipeHeating_4mmthick_PbBi_PositronTarget]]
 
  
−
==Unit conversion==
+
Question:  Will a thicker downstream exit window increase the positron production efficiency by providing more material for a brehm photon to pair produce in?
  
−
The energy deposited by photon, electrons, and positrons is predicted by GEANT4 and recorded in energy units of keV per incident electron on the PbBi target.  To convert this deposited energy to a power you need to assume a beam current.  Assuming 1 beam current of 1 mA, the conversion is given easily as
 
  
−
<math>\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) \times \left( \frac{ \mbox{e}^-}{1.6 \times 10^{-19}\mbox{C}}  \right ) \times \left( \frac{1 \times 10^{-3} \mbox{C}}{\mbox{s}} \right ) \times \left( \frac{1.6 \times 10^{-16}\mbox{W} \cdot \mbox{ s}}{\mbox{keV} }\right )</math>
+
Positrons were counted exiting a ideal 0.2 Tesla solenoid that was 15 cm long.  A ten MeV electron beam with a 0.5 cm cylindrical radius impinged a 2mm thick PbBi liquid target that had a surface area of 2.54 cm x 2.54 cm.  A 0.25 mm thick stainless steel entrance window was used. 
−
 
 
−
<math>\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) = \left( \frac{\mbox{W} }{\mbox{cm}^2 } \right )</math>
 
−
 
 
−
==Results Table==
 
  
 +
Target is at -106 mm, entrance SS window is at -108.25 mm , exit SS window is at -103.75 mm, A sensitive detector for positron is placed at Z= +44mm.  The sensitive detector is a cylinder of radius 11.74 cm.
 
 
 
{| border="1"
 
{| border="1"
 
{| border="1"
 
{| border="1"
−
| Beam Pipe Radius (mm) || Hot Spot (<math>keV/cm^2/e^-</math>)
+
| SS Exit WIndow Thickness (mm) || Positrons/Million electrons
 
|-
 
|-
−
| 34.8    || 5
+
|0.0  || 1142,1096,1149,1073,1083 = 1109 +/- 35
−
|-
+
|-
−
|  47.5    ||
+
| 0.25   || 774,836,800,785,798 = 798 +/- 23
−
|-
 
−
|   60.2   ||
 
 
|-
 
|-
−
|  72.9   ||
+
|  0.5   ||   693,704,713,697,715 = 704 +/- 10
 
|-
 
|-
−
|  97.4   ||
+
|  1.0   ||   587,606,548,592,550 =577 +/- 26
−
|-
+
|+
 
|}
 
|}
  
−
=Converter target properties=
 
  
−
Definition of Lead Bismuth
+
;Conclusion 1:  Positron production efficiency improves when the exit window is made thinner
  
 +
;Conclusion 2 : You loose about 28 +/- 4 % of the positrons in the 0.25 mm thick SS exit window.
  
−
1cm diameter target
+
=Background studies=
−
2 mm thick PbBi
 
  
−
0.5 Tesla solenoid
+
==Brem Spectrum==
  
 +
Below is the photon energy distribution (from Brem & pair production) using a 2mm Pb target for two different incident electron energies; 6 and 10 MeV.  The photons are 1 cm downstream of the target and intersection a large forward region.
  
−
Desire to know
+
[[File:PbBi_Brem_6-10MeV_4-7-16.png | 200 px]]
  
−
Emmittance (mrad * mm)
+
insert photon spacial distributions
  
−
dispersion (Delta P/P)  (mradian/1000th  mm/1000th)
+
Now move the scoring region downstream to a position representing the location of a NaI detector.
−
 
 
−
of electrons after the PbBi target.
 
−
 
 
−
 
 
−
pole face rotation in vertical plane.
 
−
 
 
−
=G4BeamLine and MCNPX=
 
−
 
 
−
 
−
==Target thickness optimization==
 
−
 
 
−
===[[PbBi_THickness_GaussBeam]]===
 
−
Dmitry's processing of Tony's GEANT simulations showing transverse phase space portrait (left) and longitudinal phase space portrait (right). Phase space portraits show coordinate x or y vs
 
−
diveregense=px/pz or py/pz (or time vs kinetic energy ). Captions show:
 
−
 
 
−
1. geometric (not normalized) emittance for transverse and emittance for longitudinal phase space portraits (ellipse areas divided by "pi")
 
−
 
 
−
2. Twiss parameters
 
−
 
 
−
3. Ellipse centroid for longitudinal phase portrait
 
−
 
 
−
4. sqrt(beta*emittance) and sqrt(gamma*emittance) - half sizes of the projections of the ellipses on the coordinate and divergence axes respectively.
 
−
 
 
−
Electrons - RMS
 
−
 
 
−
[[File:Ed1.png| 400 px]]
 
−
 
 
−
Electrons - 68.2% core
 
−
 
 
−
[[File:Ed2.png| 400 px]]
 
−
 
 
−
Positrons - RMS
 
−
 
 
−
[[File:Pd1.png| 400 px]]
 
−
 
 
−
Positrons - 68.2% core
 
−
 
 
−
[[File:Pd2.png| 400 px]]
 
−
 
 
−
=== [[PbBi_THickness_CylinderBeam]]===
 
−
Dmitry's processing of Tony's GEANT simulations showing transverse phase space portrait (left) and longitudinal phase space portrait (right). Phase space portraits show coordinate x or y vs
 
−
diveregense=px/pz or py/pz (or time vs kinetic energy ). Captions show:
 
−
 
 
−
1. geometric (not normalized) emittance for transverse and emittance for longitudinal phase space portraits (ellipse areas divided by "pi")
 
−
 
 
−
2. Twiss parameters
 
−
 
 
−
3. Ellipse centroid for longitudinal phase portrait
 
−
 
 
−
4. sqrt(beta*emittance) and sqrt(gamma*emittance) - half sizes of the projections of the ellipses on the coordinate and divergence axes respectively.
 
−
 
 
−
Electrons - RMS
 
−
 
 
−
[[File:E1.png| 400 px]]
 
−
 
 
−
Electrons - 68.2% core
 
−
 
 
−
[[File:E2.png| 400 px]]
 
−
 
 
−
Positrons - RMS
 
−
 
 
−
[[File:P1.png| 400 px]]
 
−
 
 
−
Positrons - 68.2% core
 
−
 
 
−
[[File:P2.png| 400 px]]
 
−
 
 
−
=== [[PbBi_THickness_PntSource]]===
 
−
 
 
−
Electrons and Positrons after 2mm of LBE:
 
−
 
 
−
Electrons:
 
−
 
 
−
[[File:e01.png| 200 px]][[File:e02.png| 200 px]]
 
−
 
 
−
Positrons:
 
−
 
 
−
[[File:p01.png| 200 px]][[File:p02.png| 200 px]]
 
−
 
 
−
===Energy Deposition in Target system (Heat)===
 
−
 
 
−
 
 
−
[[File:ElectronTracks.png| 200 px]][[File:PhotonTracks.png| 200 px]]
 
−
 
 
−
[[File:ElectronEnergy.png| 200 px]][[File:PhotonEnergy.png| 200 px]]
 
−
 
 
−
MCNPX simulations of energy deposition into different cells are below. There is a slight overestimate (they add up to about 120%). Positrons contribute less than 1% of electrons' contribution. No magnetic filed is assumed.
 
−
 
 
−
[[File:Model.png| 400 px]]
 
−
 
 
−
[[File:Tablen1.png| 200 px]]
 
−
 
 
−
[[File:Tablen2.png| 200 px]]
 
−
 
 
−
==Solenoid==
 
−
 
 
−
 
 
−
Inner Radiusu=
 
−
 
 
−
Outer Radius =
 
−
 
 
−
Length =
 
−
 
 
−
Current=
 
−
 
 
−
Magnetic Field Map in cylindrical coordinates (Z & R) from Niowave
 
  
 
=Beam Line Design=
 
=Beam Line Design=

Latest revision as of 21:39, 8 June 2016

Development of a Positron source using a PbBi converter and a Solenoid

Conclusions

  1. A 0.3 (0.6) Tesla Solenoid with a diameter to allow a 9.74 (3.94) cm diameter pipe would collect a positron per thousand incident electrons on a 2mm thick LBE target with 0.25 mm thick SS windows.
  2. A 15 cm long, 0.2 Tesla solenoid with a 3.94 diameter beam pipe would collect a positron per two thousand electrons impinging a 2mm thick LBE target with 0.25 mm thick SS windows.
  3. A 4 Tesla Solenoid will remove beam pipe heating from scattered electrons downstream of the target when using a 3.94 cm diameter beam pipe.

Reports

Niowave_Report_11-30-2015


deadline 4/12/16


Niowave_9-2015

Niowave_10-2015

Niowave_11-2015

Niowave_12-2015

Niowave_1-2016

Niowave_2-2016

Niowave_3-2016

Niowave_4-2016

Niowave_5-2016

Niowave_6-2016

Task List

0.) 34.8 mm pipe, 0.0 -> 0.5 Tesla, E= 6,8,10 MeV.


1.) Create a positron (10,000 positrons) and electron event file containing t,x,y,z,Px,Py,Pz for positrons exiting the solenoid and an incident Gaussian beam 1cm in diameter and with a sigma of 1cm.

compare distributions with and without solenoid.

2.) Determine the back ground when using a 3.48 diameter beam pipe and Solenoid field of 0.2 for a NaI detector placed at

3.) Experiment, install dipole and solenoid in the tunnel.

Beam Pipe Heating

PbBi_BeamPipeHeatin_2015

Converter target properties

PbBi_NioWave_TargetProperties_2015


Target thickness optimization

PbBi_THickness_CylinderBeam

PbBi_THickness_GaussBeam

PbBi_THickness_PntSource

Solenoid

Uniform ideal Solenoid

PbBi_BeamPipeHeating_w_Solenoid_2015

PbBi_60cmLong_Solenoid_Collection_Efficiency_2015

Positron & Electron event files

PbBi_PosEventFiles_VaccumGaps_2015

PbBi_PosEventFiles_NoGaps_2016

Solenoid Map

Inner Radiusu=

Outer Radius =

Length =

Current=

Magnetic Field Map in cylindrical coordinates (Z & R) from Niowave

Rear Window Thickness

Question: Will a thicker downstream exit window increase the positron production efficiency by providing more material for a brehm photon to pair produce in?


Positrons were counted exiting a ideal 0.2 Tesla solenoid that was 15 cm long. A ten MeV electron beam with a 0.5 cm cylindrical radius impinged a 2mm thick PbBi liquid target that had a surface area of 2.54 cm x 2.54 cm. A 0.25 mm thick stainless steel entrance window was used.

Target is at -106 mm, entrance SS window is at -108.25 mm , exit SS window is at -103.75 mm, A sensitive detector for positron is placed at Z= +44mm. The sensitive detector is a cylinder of radius 11.74 cm.

SS Exit WIndow Thickness (mm) Positrons/Million electrons
0.0 1142,1096,1149,1073,1083 = 1109 +/- 35
0.25 774,836,800,785,798 = 798 +/- 23
0.5 693,704,713,697,715 = 704 +/- 10
1.0 587,606,548,592,550 =577 +/- 26


Conclusion 1
Positron production efficiency improves when the exit window is made thinner
Conclusion 2
You loose about 28 +/- 4 % of the positrons in the 0.25 mm thick SS exit window.

Background studies

Brem Spectrum

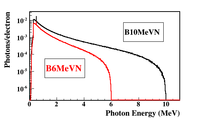
Below is the photon energy distribution (from Brem & pair production) using a 2mm Pb target for two different incident electron energies; 6 and 10 MeV. The photons are 1 cm downstream of the target and intersection a large forward region.

PbBi Brem 6-10MeV 4-7-16.png 

insert photon spacial distributions

Now move the scoring region downstream to a position representing the location of a NaI detector.

Beam Line Design

PbBi_BeamLine_Elements

goals for JLab

Positrons#Simulations

Retrieved from "https://wiki.iac.isu.edu/index.php?title=G4Beamline_PbBi&oldid=106437"