[math]\underline{\textbf{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
Test for [math]\theta=20[/math] and [math]\phi=0[/math]
Substituting in the values found earlier for the case of [math]\theta=20^{\circ}[/math] and [math]\phi=0[/math]
[math]a=\frac{a_1+a_2}{2}=1.0459[/math]
[math]e\equiv \frac{sin(25^{\circ})}{cos(\theta)}= \frac{sin(25^{\circ})}{cos(20^{\circ})}=.4497[/math]
[math]x_1^'=\frac{r_2^{'2}-r_1^{'2}}{4ae}-ae=\frac{r_2^{'2}-r_1^{'2}}{4(1.0459)(.4497)}-(1.0459)(.4497)[/math]
Since
[math]\lVert \overrightarrow{D1P} \rVert \equiv \lVert \overrightarrow{F1P} \rVert \qquad \qquad \lVert \overrightarrow{D2P} \rVert \equiv \lVert \overrightarrow{F2P} \rVert[/math]
[math]D1P \approx .576\ \text{m}\qquad D2P \approx 1.516\ \text{m}[/math]
The [math]x_1^' [/math] distance from focal point 1 is:
[math]x_1^'=\frac{1.516^2-.576^2}{4(1.0459)(.4497)}-(1.0459)(.4497)=\frac{1.97}{1.88}-.4703=.576\ \text{m}=r_1[/math]
This is the radius from focal point 1, which is to be expected since the y component is equal to zero for [math]\phi=0[/math]
The focii are located at
[math]F1\equiv (-\Delta a+ae,0)=(-.1775+1.0459(.4497),0)=(.292,0)\ \text{m}\qquad F2\equiv (-\Delta a-ae,0)=(-.1775-1.0450(.4497),0)=(-6.478,0)\ \text{m}[/math]
This implies that with respect to the origin, x', we find
[math]x'=x_1'+\Delta a+ae=.576+.292=.868\ \text{m}[/math]
This is verified with CED
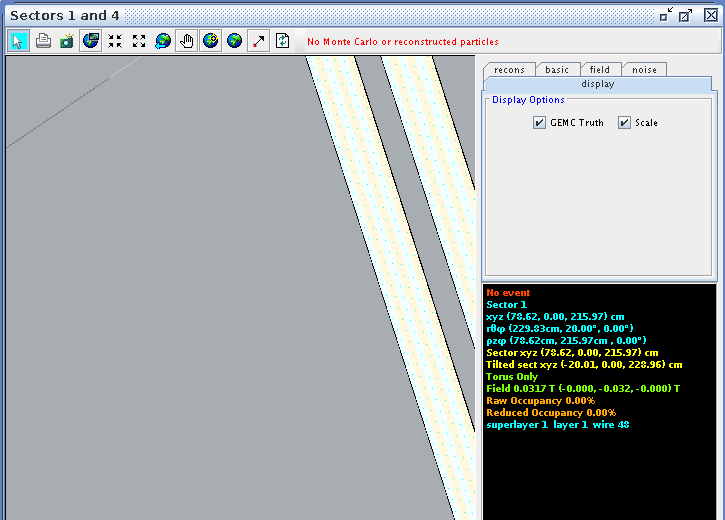
Since the x' dimension is the hypotenuse in a right triangle of 65 degrees
[math]x'=\frac{x_{lab}}{sin 65^{ \circ}}=.868=x'[/math]
[math]\underline{\textbf{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]

