In the Detector Plane
In the plane
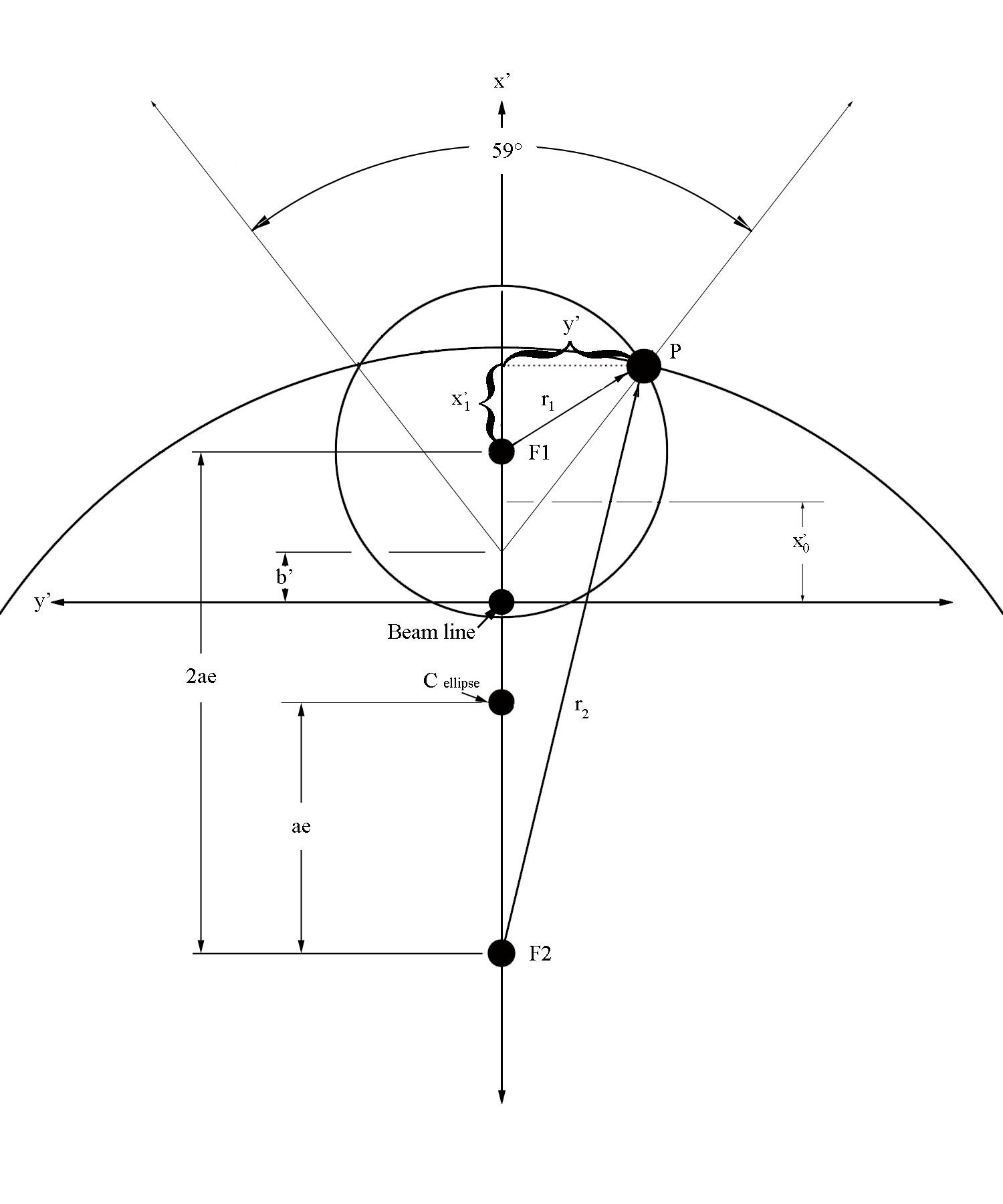
We can use the geometry of the sector to impose limits on the allowed x and y for this plane. The angle which the two sides of the triangle that make up the sector is given as . Each focii will have a ray that creates a circle around the point that is equal to the length found from the D1P and D2P lines. These circles will overlap at a common y component, which can be used to determine if the point is within the detector limits.
Using the physical constraints of the distance the interior walls of the side walls intersect each other from the beam line, as well as the angle the lowest guard wire at the plane midpoint.
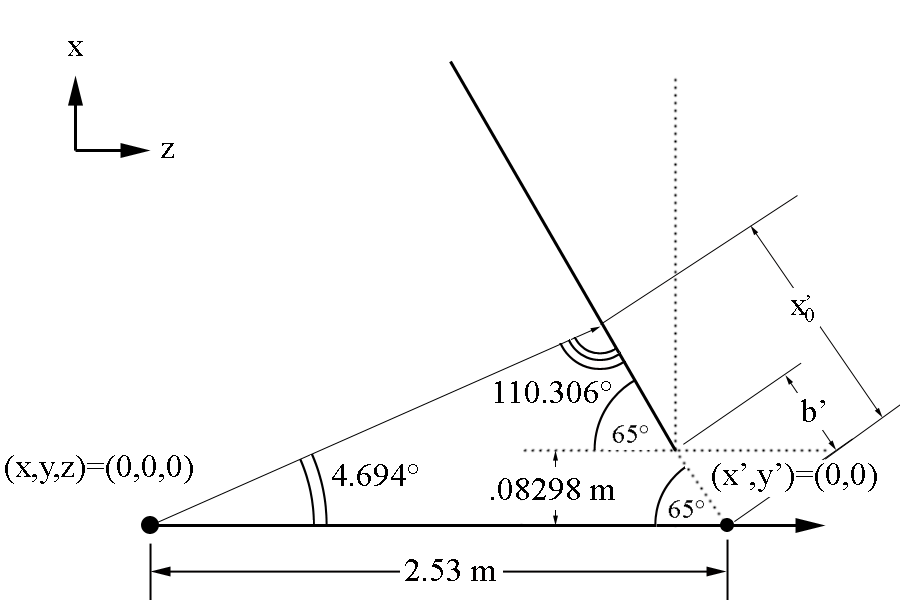
where b' is the location on the y' axis where the two interior side walls of the sector intersect.
The quantity is the corresponding x' distance from the beam line and detector plane intersection.
Since the interior sides of the sector make an angle of in the plane of the wires, this can be represented by equations
Using the properties of an ellipse, we can work in the coordinates of the ellipse, in the plane of the ellipse, where the vertex is located at the crossing of the ellipse and the cone. Since the Dandelin construction was used, we know that
If we shift the origin from the center of the ellipse to the intersection of the plane and cone for a given theta
Writing the equations for circles centered at an ellipse focii points, we find
Since the focii are seperated by 2ae as found earlier