Difference between revisions of "DV RunGroupC Moller"
| Line 189: | Line 189: | ||
<center><math>\ell \equiv </math>length of target</center> | <center><math>\ell \equiv </math>length of target</center> | ||
| + | |||
| + | |||
| + | <center><math>dN=\frac{dR}{dt}=\mathcal L \times \sigma_p</math></center> | ||
Revision as of 19:18, 6 September 2016
need to insert moller shielding into card after moller LUND file is created. (see clas12/beamline)
Simulating the Moller scattering background for EG12
Moller Differential Cross-Section
GEANT4 Simulation of Moller Events
Simulation Setup
Use GEANT4 via GEMC to estimate the Moller background for electron scattering experiments in JLab's Hall B. The first step towards this goal is to use GEANT4 without the GEMC infrastructure to create event (LUND) files that will be used as input events for GEMC.
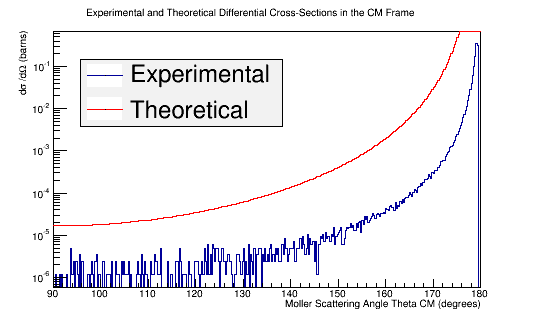
Benchmark GEANT4's Moller scattering prediction with the theoretical cross section using LH2
Comparison of simulation vs. the theoretical Møller differential cross section using 11 GeV electrons impinging LH2
Change to a NH3 Target
Replacing the LH2 target with an NH3 target
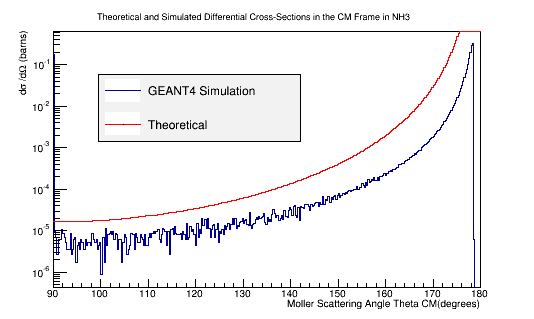
Benchmark GEANT4's Moller scattering prediction with the theoretical cross section using NH3
Comparison of simulation vs. the theoretical Møller differential cross section using 11 GeV electrons impinging NH3
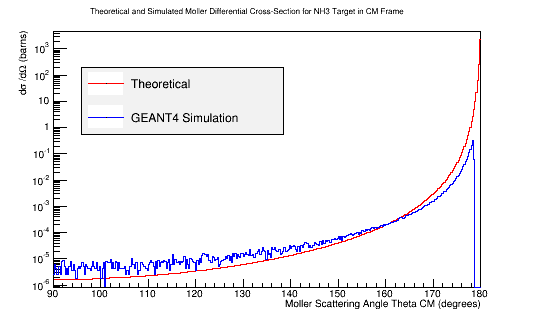
LH2 Vs. NH3
Benchmark GEANT4's Moller scattering prediction for NH3 and LH2
Effects Due to Target Material
Target Density
Atomic Mass and Electron Number Effects
Differential Cross-Section Offset
ROOT Macro to read LUND files and make plots
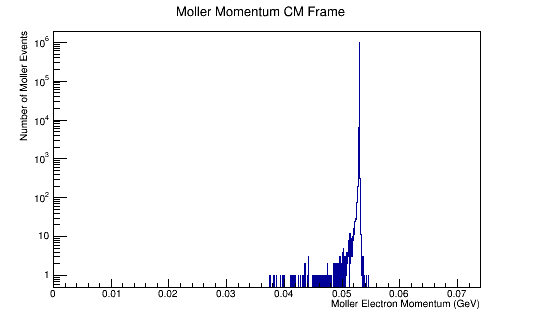
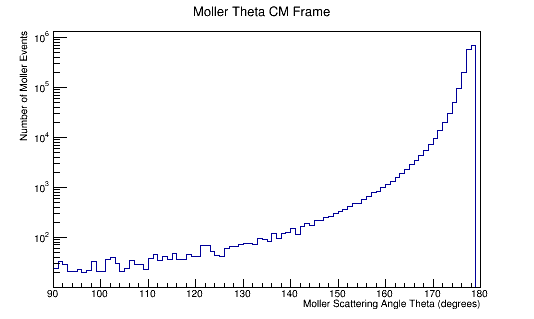
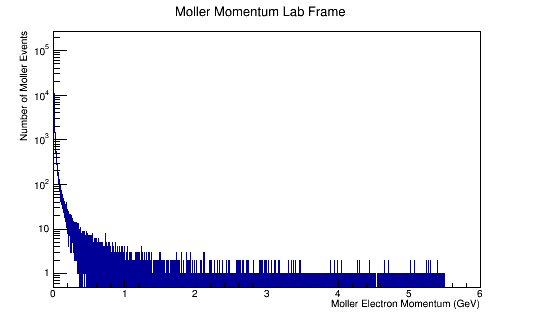
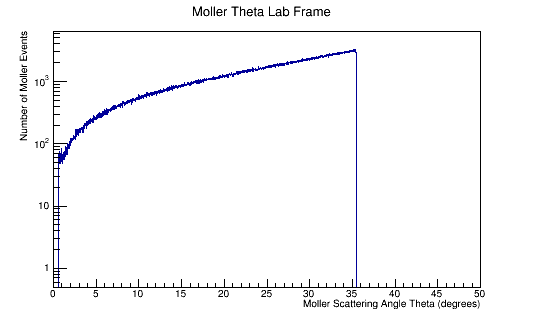
Run the above theta and E distribution of Mollers through GEMC with and without Solenoid on. Determine the Theta and E range of Mollers that enter the detector.
Scanning from 2MeV to 5500MeV, and 0 to 36 degrees in Theta.
For Solenoid on with 5T:
<gcard>
<detector name="../../../../../clas12/fc/forwardCarriage" factory="TEXT" variation="original"/>
<detector name="../../../../../clas12/dc/dc" factory="TEXT" variation="original"/>
<detector name="../../../../../clas12/ec/ec" factory="TEXT" variation="original"/>
<detector name="../../../../../clas12/ctof/ctof" factory="TEXT" variation="original"/>
<detector name="../../../../../clas12/ftof/ftof" factory="TEXT" variation="original"/>
<detector name="../../../../../clas12/htcc/htcc" factory="TEXT" variation="original"/>
<detector name="../../../../../clas12/pcal/pcal" factory="TEXT" variation="original"/>
<option name="BEAM_P" value="e-, 2.800*GeV, 18.0*deg, 10*deg"/>
<option name="SPREAD_P" value="2.798*GeV, 18*deg, 180*deg"/>
<option name="SCALE_FIELD" value="clas12-torus-big, -1.0"/>
<option name="HALL_FIELD" value="clas12-solenoid"/>
<option name="SCALE_FIELD" value="clas12-solenoid, 1.0"/>
<option name="OUTPUT" value="evio,eg12.ev"/>
</gcard>
Using the standard commands for gemc
gemc -USE_GUI=0 -N=1000 eg12_sol.gcard ~/src/CLAS/coatjava-1.0/bin/clas12-reconstruction -i eg12.ev -config DCHB::torus=-1.0 -config DCHB::solenoid=1.0 -config DCTB::kalman=true -o eg12_rec.ev -s DCHB:DCTB:EC:FTOF:EB ~/src/CLAS/coatjava-1.0/bin/run-groovy Analysis.groovy eg12_rec.0.evio
Checking for a reconstructed particle that undergoes a phi shift where the 1st column is energy and the 2nd the scattering angle theta:
For Energy:
awk 'NR == 1 {line =$0; min =$2} NR >1 && $2 < min {line =$0; min = $2} END{print line}' Energy_Phi_Shift.dat
289 0.6624017631112946 33.37507824033966 -179.63657653407975 0.7254709 29.696417 -177.79057 473.36051689004984 11.978802748439216 -129.55774724876173
awk 'NR == 1 {line =$0; max =$2} NR >1 && $2 > max {line =$0; max = $2} END{print line}' Energy_Phi_Shift.dat
978 5.584765946130235 24.90893565820338 -170.69784116534063 5.593401 24.90894 -170.65994 472.16552666546283 23.31807917059094 -165.11125601370114
For Theta:
awk 'NR == 1 {line =$0; min =$3} NR >1 && $3 < min {line =$0; min = $3} END{print line}' Energy_Phi_Shift.dat
12 4.83485521395583 10.577021312967325 -50.86708775351051 4.8205996 10.617784 -50.895683 491.627055439108 5.9032309421001985 -43.82964507576243
awk 'NR == 1 {line =$0; max =$3} NR >1 && $3 > max {line =$0; max = $3} END{print line}' Energy_Phi_Shift.dat
187 1.3382869250001856 35.63598792463312 29.887530073265214 1.3481133 35.449417 30.009071 472.455052447561 19.034043420497742 55.20328358414997
Similarly for 0T:
For Energy:
awk 'NR == 1 {line =$0; min =$2} NR >1 && $2 < min {line =$0; min = $2} END{print line}' Energy_Phi_Shift.dat
148 0.36418038435234207 33.68296595663359 -175.89942431595827 0.35383263 51.743824 -39.45801 469.5694572319308 24.353383233947522 -176.27025218702502
awk 'NR == 1 {line =$0; max =$2} NR >1 && $2 > max {line =$0; max = $2} END{print line}' Energy_Phi_Shift.dat
818 5.5278794590742235 12.937136966282836 -43.35663621477178 5.539351 12.95216 -49.09295 484.8800252169308 8.27731670021694 -43.245753766203364
For Theta:
awk 'NR == 1 {line =$0; min =$3} NR >1 && $3 < min {line =$0; min = $3} END{print line}' Energy_Phi_Shift.dat
559 4.909449160222199 9.918634647646794 0.06548256930681198 4.914272 9.938521 -5.861595 492.1448533455858 7.501204563534799 -0.006721611135017764
awk 'NR == 1 {line =$0; max =$3} NR >1 && $3 > max {line =$0; max = $3} END{print line}' Energy_Phi_Shift.dat
326 1.272966353429713 35.731680814303196 85.3173707349696 1.2830343 38.27654 58.368687 483.4835073848272 3.950855595379657 83.87603767806992
Reconstruction of Moller Events
The LUND format
Writing LUND files
Running GEMC
Phi Shift observation using DC hit Reconstruction Data
Gcard creation defining energy and angle range of electrons
Modified gcards
Effects of Solenoid on Electrons
Results for defined distribution in Solenoid Fields
Results for Random Spread of Energy and angle theta in the Lab frame
Cover Full Solid Angle of Detector
Using GEANT simulation data
Calculations of 4-momentum components
Alter Phi Angles
Check Differential Cross-Section
Using Isotropic spread in Theta and Energy for Set Angle Phi
Since the Differential Cross-Section for Moller scattering is well known in the center of mass frame of reference, a conversion to the detector's lab frame of reference will need to occur. To ensure that the GEMC detector is fed a Moller LUND file for the differential cross section, the center of mass frame LUND information must be converted to the lab frame equivalent. Using the expression for the differntial cross-section:
where,
A beam of electrons with a constant energy impinging on a stationary electron in the lab frame can be converted to the center of mass frame energies which by definition must be equal. Since the Energy in the CM frame is constant in so long as the incoming electron energy is constant, we should be able to cycle through only the scattering angle theta to obtain the differential cross-section.
For the GEMC detector to simulate a given distribution, a LUND file must be created. LUND files can pass information about position and momentum, but not angle, in the lab frame. Assuming a constant position at the vertex, this implies that we will need to cycle through the momentum components for the scattered and Moller electrons in the CM frame to vary angle theta in the lab frame. The CM frame also implies that the total momentum for the scattered and Moller electron be equal but opposite.
From the definition of the differential cross-section:
where
Uniform distribution in Energy and Theta LUND files
Reading LUND files
Run in GEMC
Detector Occupancy
clas12->Draw("Detector.wire:Detector.layer>>(7,1,7,120,0,120)","Detector.superlayer<3","colz")
Gcard settings
Verfication of Mother/Daughter Occupancy
Benchmark GEMC Occupancy Prediction for 11GeV Electron Beam with 0T Solenoid for LH2
Setup for Batch Job With Varying Experimental CLAS12 Quantities
Run Occupancy for Sector 1 DC hits
Papers used
[1]Farrukh Azfar's Derivation of Moller Scattering
A polarized target for the CLAS detector
An investigation of the spin structure of the proton in deep inelastic scattering of polarized muons on polarized protons
QED Radiative Corrections to Low-Energy Moller and Bhabha Scattering
http://arxiv.org/abs/1602.07609