[math]\textbf{\underline{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
4.1.5 Weight
Using the theoretical differential cross section from previous
[math]\frac{d\sigma}{d\Omega}=\frac{ \alpha^2 }{4E^2}\frac{ (3+cos^2\theta)^2}{sin^4\theta}[/math]
[math]\alpha ^2=5.3279\times 10^{-5}[/math]
[math]E\approx 53.013 MeV[/math]
We can take the Moller electron distribution of Theta in the Center of Mass frame, and multiply each given angle Theta by the expected differential cross section.
This causes the Moller Theta distribution in the Center of Mass frame to directly follow the theoretical differential cross section.
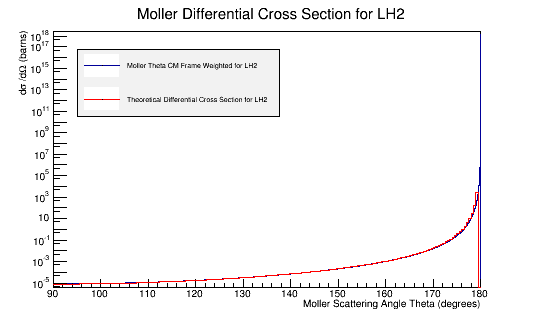
The Lab frame distribution of Theta can also be weighted similarly. However, instead of having it be a differential cross section, we can find the necessary number of particles.
[math]\frac{d\sigma}{d\Omega} = \frac{\left(\frac{number\ of\ particles\ scattered/second}{d\Omega}\right)}{\left(\frac{number\ of\ incoming\ particles/second}{cm^2}\right)}=\frac{dN}{\mathcal L\, d\Omega} =differential\ scattering\ cross\ section[/math]
[math]\frac{d\sigma}{d\Omega} =\frac{dN}{\mathcal L\, d\Omega} =\frac{dN}{\Phi \rho \ell\, d\Omega}[/math]
[math]\Rightarrow \int \frac{d\sigma}{d\Omega} \rho\ \ell \Phi d\Omega=\int dN[/math]
Checking versus the given Luminosity for the experiment
[math]\mathcal L = \frac{1.33 \times 10^{35}}{cm^2\cdot s} \times \frac{10^{-24} cm^2}{barn}=1.33\times 10^{11} barns^{-1}s^{-1}[/math]
[math]\mathcal L \int \frac{d\sigma}{d\Omega} d\Omega = 1.33 \times 10^{11} barns^{-1} \times 2\pi\ \int \frac{d\sigma}{d\Omega}\ \sin{\theta} d\theta=N[/math]
Limiting the range of Theta to within 5 to 40 degrees in the Lab frame:
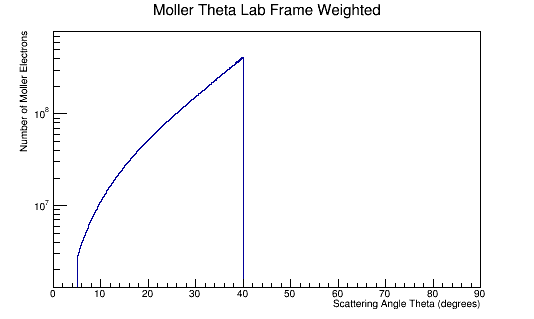
We can find the corresponding angular range in the CM frame:
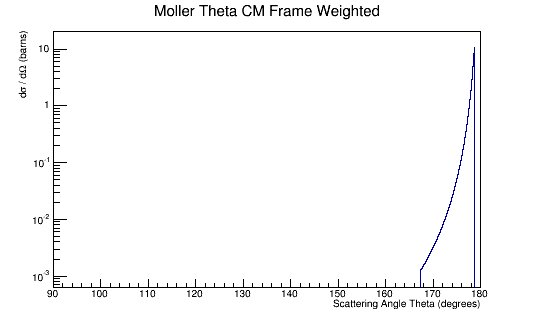
Integrating the differential cross-section over the solid angle:
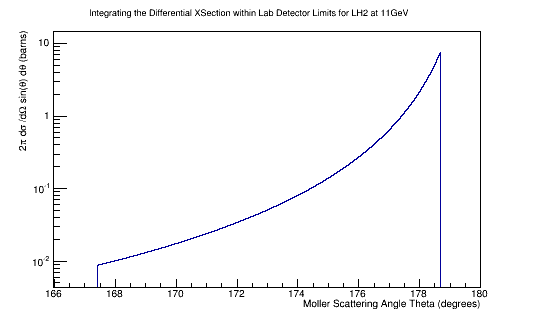
IntegralDiffXSect->Integral()
4.97493824519086629e+04 barns
Multiplying by the Luminosity, we find:
[math]4.97\times 10^{4} barns \times\frac{1.35\times 10^{11}}{barns\cdot s}=6.71\times 10^{15}\frac{electrons}{s}[/math]
[math]\textbf{\underline{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]




