Points of Intersection
Points of Intersection
Since the wires are above the y axis in the x-y plane, we can use a rotation matrix about the z axis, to rotate points and equations into the coordinate system of the wire (x, y). There are two types of rotation matrix which are referred to as a passive or active transformation matrices. The passive transformation takes the components of a vector in the first system and finds the components of this vector in a new system. In effect, this type of transformation rotates the coordinate system while leaving the vector stationary. An active transformation matrix uses the original basis vectors to find the basis vectors in the new system. The outcome of this is to in effect rotate the vector to a different coordinate system.
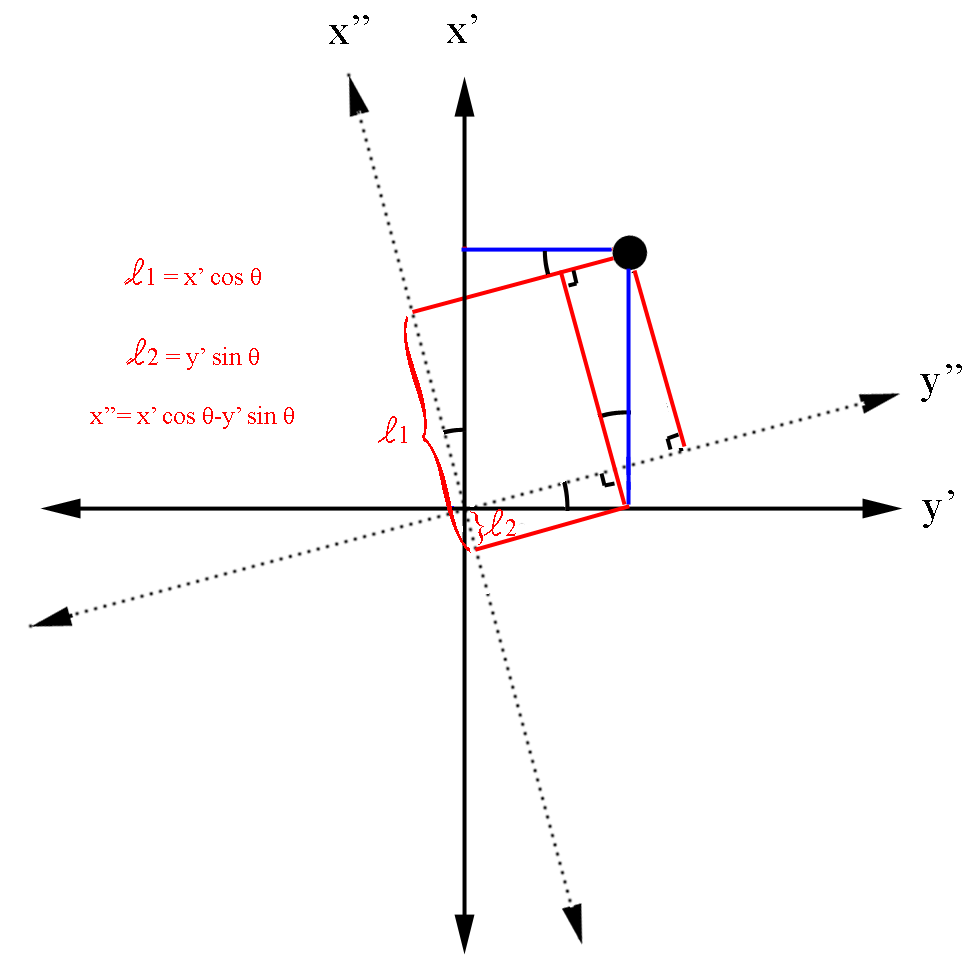
Demonstrating a passive rotation for a point in space we can use the rotation matrix
which corresponds to a counter-clockwise rotation of a positive angle \[Theta] in the x-y plane. In determining that the angle is positive, this dictates the rotation must be from the x towards the y axis in the 1st quadrant. By the orthogonality of the Cartesian coordinates this then gives positive \[Theta] rotations from the y to -x in the 2nd, the -x to the -y in the 3rd, and -y to x axis in the 4th quadrants. This then implies a clockwise rotation from the x to the -y axis with a negative angle in the xy plane, for the 1st and so forth for the remaining quadrants in the x-y plane. Since the even odd properties of the sine and cosine functions with respect to the input angle determine the sign of the function, we find
with
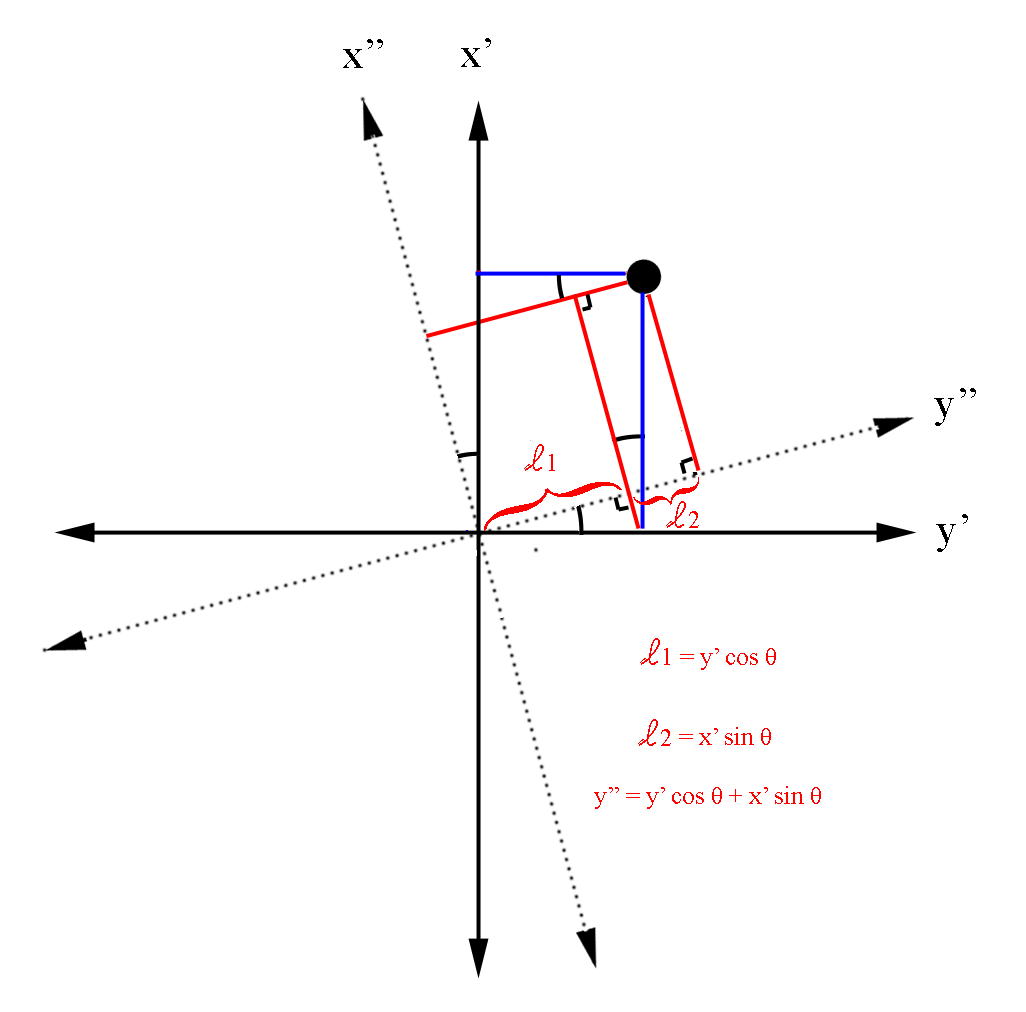
Conversely, a negative rotation can be viewed as a positive rotation of from the y towards the x axis in the 1st quadrant for the y-x plane.
This positive rotation will correspond to a counter-clockwise rotation, just as a negative rotation will correspond to a clockwise one in the y-x plane.
Checking with the geometry, we find for a counter-clockwise rotation in the y-x plane:
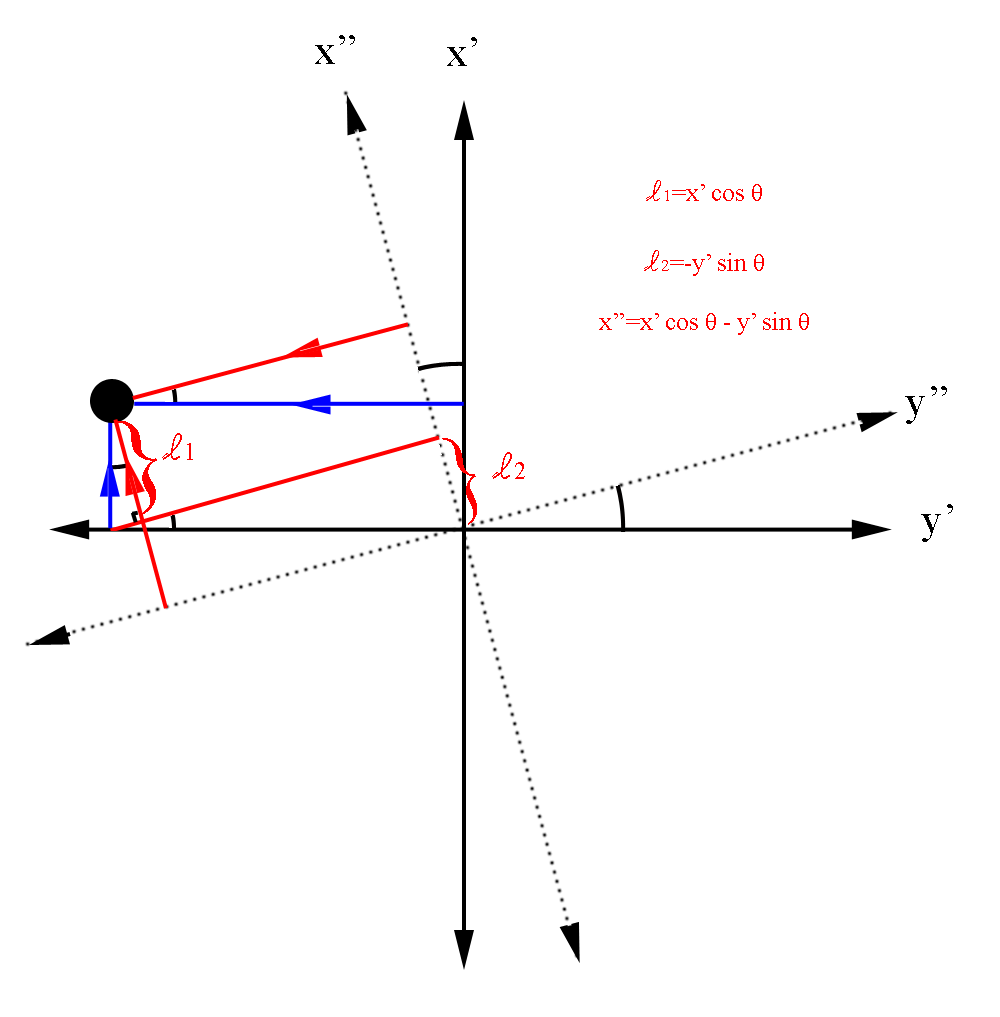
For the 1st quadrant, as expected for a positive rotation from y to x axis in the y-x plane. Again, this corresponds to a negative in the x-y plane, with
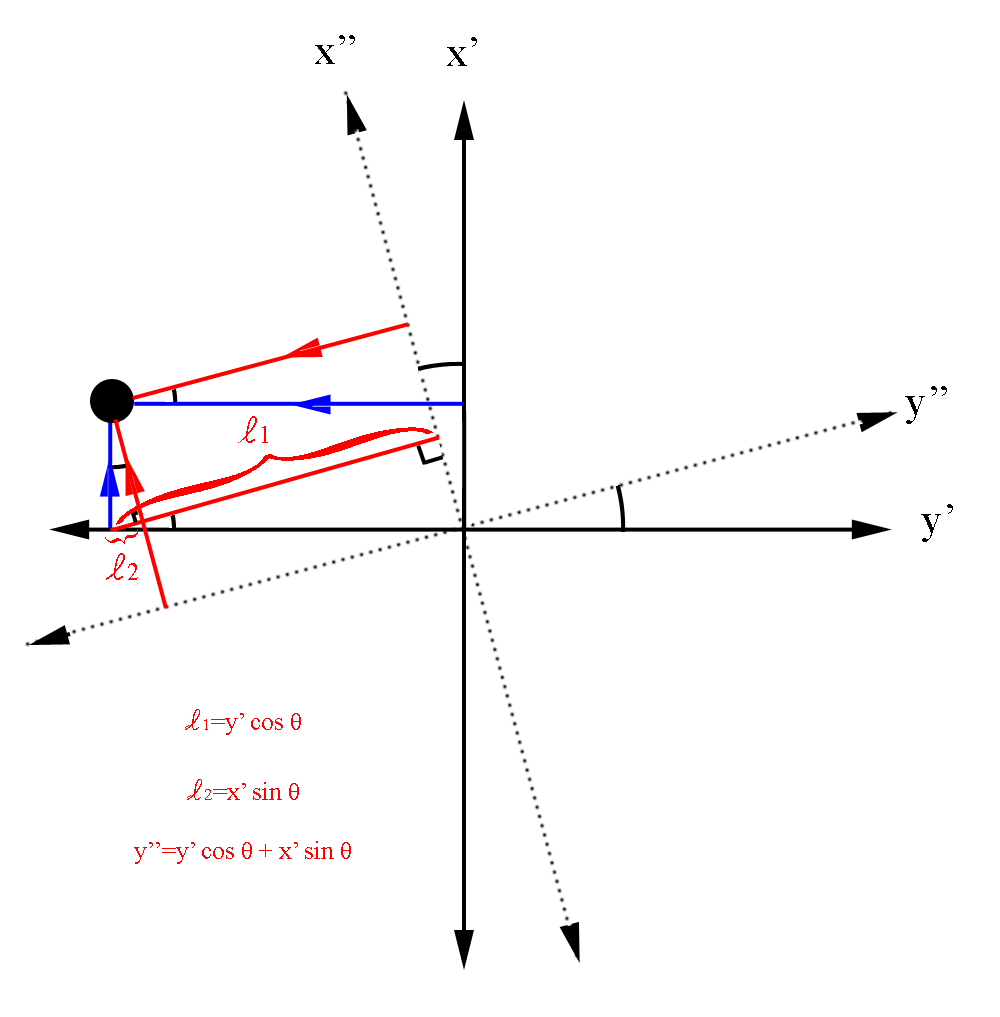
For the 4th quadrant, where y is negative,
as expected for a positive rotation from x to -y axis in the y-x plane. Again, this corresponds to a negative in the x-y plane, with