Difference between revisions of "HRRL Positron Rotating W Target"
| (131 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | [[PositronTargetWorkByChrissJackson]] | |
| − | + | ||
| − | + | =Target Construction= | |
| − | + | ||
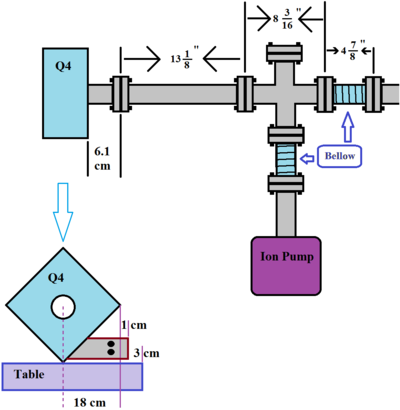
| + | Current beam line distances for target to be inserted into | ||
| + | |||
| + | [[File:hrrl_e+_Target_area_Space.png | 400 px]] | ||
| + | |||
| + | ==Motor== | ||
| + | |||
| + | [[File:HRRL_Beam_Rot_Tar_Sys_Mot1.png | 400 px]] | ||
| + | |||
| + | Empire Magnetics Model U42 | ||
| + | |||
| + | ;Wiring Diagram:[[Media:U-42EmpireMagneticsMotorWiringDiag.pdf]] | ||
| + | |||
| + | [http://www.youtube.com/watch?v=pS0cBeT_trE&context=C41942f6ADvjVQa1PpcFPVZGpWjIhpT6B3B7hDLZHuaQKYXRQ0xVc= Motor test video 1] | ||
| + | |||
| + | [http://www.youtube.com/watch?v=En2mQlIkufA&context=C489b379ADvjVQa1PpcFPVZGpWjIhpT2TjUnFPiVQJteDyjBCk9cg= test video 2] | ||
| + | |||
| + | [http://www.youtube.com/watch?v=jeV11UtdtxU&context=C4b683ecADvjVQa1PpcFPVZGpWjIhpT3wsAPHTaPLebK8Mca7ahRg= test video 3] | ||
| + | |||
| + | [http://www.youtube.com/watch?v=PVv4XavFNfw&context=C4645105ADvjVQa1PpcFPVZGpWjIhpT_b2hBEuqINhOmJtWj57qxg= test video 4] | ||
| + | |||
| + | [http://www.youtube.com/watch?v=VeXNV1EX5Vc&context=C4d73946ADvjVQa1PpcFPVZGpWjIhpT6B3B7hDLZHuaQKYXRQ0xVc= test video 5] | ||
| + | |||
| + | ==Motor Controller== | ||
| + | |||
| + | ===Power supply=== | ||
| + | |||
| + | [http://www.lamonde.com/acatalog/Products_Power_Supplies_992.html#aSTP_2dPWR_2d4810 Power Supply STP-PWR-4810 Power supply for stepping systems, dual output with 48 VDC @ 10A (at full load) unregulated and 5 VDC at 0.5A regulated.] | ||
| + | |||
| + | ===STR8 === | ||
| + | |||
| + | [[file:STR8.png | 300 px]] | ||
| + | |||
| + | STR8 Manuals: | ||
| + | |||
| + | [[Media:STR_Hardware_Manual.pdf]] | ||
| + | |||
| + | [[Media:STR_Quick_Setup_Guide.pdf]] | ||
| + | |||
| + | Datasheet: | ||
| + | |||
| + | [[Media:STR_Brochure_925-0002_RevC.pdf]] | ||
| + | |||
| + | =Design= | ||
| + | |||
| + | == Documents == | ||
| + | |||
| + | [[File:BRACKET_TUBE_END_SUPPORT_1.pdf]] | ||
| + | |||
| + | [[File:CAP_FITTING.pdf]] | ||
| + | |||
| + | [[File:CONE_TAPER_LOCK.PDF]] | ||
| + | |||
| + | [[File:COOLING_COOL_A_HELICAL.PDF]] | ||
| + | |||
| + | [[File:FERRULE_1.PDF]] | ||
| + | |||
| + | [[File:FITTING_ASSY_1_ISO_CUT_AWAY_2.PDF]] | ||
| + | |||
| + | [[File:FITTING_MAIN_BODY.PDF]] | ||
| + | |||
| + | [[File:HOSE_CLAMP.PDF]] | ||
| + | |||
| + | [[File:HUB_PEMSERT_ASSY.PDF]] | ||
| + | |||
| + | [[File:HUB_TAPER_LOCK.PDF]] | ||
| + | |||
| + | [[File:S VSRH_U42_RTD_110726A_SYSTEM_LAYOUT.pdf]] | ||
| + | |||
| + | [[File:S VSRH_U42_RTD_HS.PDF]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ==45 degree angle== | ||
| − | The | + | The Tungsten target should make a 45 degree angle with the beam. |
| − | + | make the motor so it can be rotated. | |
| − | + | ==Beam Heat Load== | |
| − | =Beam Heat Load= | ||
;Accelerator Settings | ;Accelerator Settings | ||
| Line 45: | Line 105: | ||
''P'' = (10 MeV) <math>\times</math> (60 <math>\mu</math>A) = 600 Watts. | ''P'' = (10 MeV) <math>\times</math> (60 <math>\mu</math>A) = 600 Watts. | ||
| − | = Properties of Tungsten= | + | ==Target Chamber design== |
| + | |||
| + | Latest Design From empire and Sadiq's measurement of the available space | ||
| + | |||
| + | |||
| + | |||
| + | {| border="1" cellpadding="20" cellspacing="0" | ||
| + | |- | ||
| + | |[[File:EmpMagHRRLPositronTargetChamberDrw_9-20-11.png | 200 px]]||[[File:HRRLPositronTargetSpace_10-5-11.png | 200 px]] || [[File:HRRLPositronTargetCoupler_10-5-11.png | 200 px]]|| [[File:HRRLPositronTargetHub_10-5-11.png | 200 px]] | ||
| + | |- | ||
| + | | Target motor Design || Available beam line space || Motor axle coupling to rotary union || Hub and spline to attache targets | ||
| + | |} | ||
| + | |||
| + | |||
| + | ;Dimensions are in inches | ||
| + | |||
| + | [[File:HRRLPositronTargetChamber_4-20-11.png | 200 px]] | ||
| + | |||
| + | There is an 18" space in Z for the target chamber. If you want to rotate a disk on the 5" wide motor you will need at least a a 10" x 10" area. | ||
| + | |||
| + | So we could try as a first design a chamber which is 18" x 15" x 15". | ||
| + | We need the following | ||
| + | |||
| + | *2 beam flanges flush with the walls of the chamber. | ||
| + | *2 flanges to allow access for hands to work on the target motor inside. It should able to fit hands through. | ||
| + | *a flange on top which will allow a 10" diameter target disk to come out. | ||
| + | *a flange on the bottom for the ion pump. | ||
| + | |||
| + | |||
| + | |||
| + | July Design From empire | ||
| + | |||
| + | [[File:EmpMagHRRLPositronTargetChamberDrw_7-25-11.png | 200 px]] | ||
| + | |||
| + | {| border="1" cellpadding="20" cellspacing="0" | ||
| + | |- | ||
| + | |[[File:EmpMagHRRLPositronTargetChamberPict_7-25-11.png | 200 px]]||[[File:EmpMagStatorCoolLines_7-26-11.png | 200 px]] | ||
| + | |- | ||
| + | | Rotary Union overlayed on conceptual drawing. || Conceptual drawing of stator cooling lines. We will need separate connection to them on the vacuum chamber. | ||
| + | |} | ||
| + | |||
| + | ==Gate Valve - Target distance== | ||
| + | |||
| + | The distance from the front of the gate valve to the most beam upstream part of the target chamber is | ||
| + | |||
| + | 88.43 cm | ||
| + | |||
| + | The gate valve closes in 0.7 sec. | ||
| + | |||
| + | |||
| + | So water would need to travel at a speed of 88.43 cm/0.7 sec = 1.26 m/sec | ||
| + | |||
| + | == Properties of Tungsten== | ||
*Melting Point = 3695 K. | *Melting Point = 3695 K. | ||
| Line 56: | Line 168: | ||
*Heat loss due to radiation: ( \sigma T^4) | *Heat loss due to radiation: ( \sigma T^4) | ||
| − | =Tungsten Temperature as a function of heat load= | + | ==Tungsten Temperature as a function of heat load== |
*IAC beamline pressure = <math>10^{-8} </math> Torr | *IAC beamline pressure = <math>10^{-8} </math> Torr | ||
| Line 64: | Line 176: | ||
*Conduction and Radiation | *Conduction and Radiation | ||
| − | =Calculating Radiators Equilibrium Temperature= | + | ==Calculating Radiators Equilibrium Temperature== |
| − | ==1.Calculating number of particles per second == | + | ===1.Calculating number of particles per second === |
We have electron beam of: | We have electron beam of: | ||
| Line 91: | Line 203: | ||
| − | ==2.Calculating Energy deposited per second== | + | ===2.Calculating Energy deposited per second=== |
If we find the energy deposited by each electron and multiply to the total number of electrons in each second, we will find the total energy per second deposited in radiator. | If we find the energy deposited by each electron and multiply to the total number of electrons in each second, we will find the total energy per second deposited in radiator. | ||
| Line 106: | Line 218: | ||
Stopping power can be found from nuclear data tables <math> (dE/dx)_{ave} </math> and thickness is 0.001 times of radiation length. From Particle Data group we got radiation length and average total stopping powers around 15MeV for electrons in these materials from National Institute of Standards and Technology: [http://physics.nist.gov/PhysRefData/Star/Text/ESTAR.html Tungsten Stopping Power]. | Stopping power can be found from nuclear data tables <math> (dE/dx)_{ave} </math> and thickness is 0.001 times of radiation length. From Particle Data group we got radiation length and average total stopping powers around 15MeV for electrons in these materials from National Institute of Standards and Technology: [http://physics.nist.gov/PhysRefData/Star/Text/ESTAR.html Tungsten Stopping Power]. | ||
| − | ===Table of Radiation Lengths=== | + | ====Table of Radiation Lengths==== |
Note:These data is from Particle Data group,Link: [http://pdg.lbl.gov/AtomicNuclearProperties/]. | Note:These data is from Particle Data group,Link: [http://pdg.lbl.gov/AtomicNuclearProperties/]. | ||
| Line 120: | Line 232: | ||
|}<br> | |}<br> | ||
| − | ===Table of energy calculations=== | + | ====Table of energy calculations==== |
For the thickness of 0.001 Radiation Length (0.0001RL) of radiators. | For the thickness of 0.001 Radiation Length (0.0001RL) of radiators. | ||
Note: <math>(dE/dx)_{coll}</math> is from National Institute of Standards and Technology. Link: [[http://physics.nist.gov/PhysRefData/Star/Text/ESTAR.html]]) | Note: <math>(dE/dx)_{coll}</math> is from National Institute of Standards and Technology. Link: [[http://physics.nist.gov/PhysRefData/Star/Text/ESTAR.html]]) | ||
{| border="1" cellpadding="20" cellspacing="0" | {| border="1" cellpadding="20" cellspacing="0" | ||
| − | |||
| − | |||
|- | |- | ||
|Elements | |Elements | ||
| Line 142: | Line 252: | ||
<math>P_{dep}= E_{dep}/s = ( E_{(dep~by~one)})\times(Number~of~electrons~per~second)</math> | <math>P_{dep}= E_{dep}/s = ( E_{(dep~by~one)})\times(Number~of~electrons~per~second)</math> | ||
| − | ==3.Calculating equilibrium temperature using Stefan–Boltzmann law== | + | ===3.Calculating equilibrium temperature using Stefan–Boltzmann law=== |
If we assume that there is no energy conduction and total energy is just radiated from two surfaces of the radiators which are as big as beam spot,in our case beam spot is 2mm in diameter. According to Stefan–Boltzmann law, this total power radiated will be | If we assume that there is no energy conduction and total energy is just radiated from two surfaces of the radiators which are as big as beam spot,in our case beam spot is 2mm in diameter. According to Stefan–Boltzmann law, this total power radiated will be | ||
| Line 157: | Line 267: | ||
| − | =Vendors= | + | ==Vendors== |
| + | |||
| + | |||
| + | ===MDC Target Chamber=== | ||
| + | |||
| + | Target chamber: MDC vacuum products can send a prefab one you just need to weld up. | ||
| + | |||
| + | John Brooks | ||
| + | |||
| + | jbrooks@mdcvacuum.com | ||
| + | |||
| + | |||
| + | |||
| + | 1-800-443-8817 | ||
| + | |||
| + | or | ||
| − | ==Tungsten Disks== | + | 510-265-3569 |
| + | |||
| + | [[File:TargetChamberDesign_1.0.pdf]] | ||
| + | |||
| + | Tom Bogden (John's boss) | ||
| + | |||
| + | |||
| + | MDC does not have a fast closing gate valve. Model GV1500 closes in 0.7 seconds and costs $1600. One that closes in 10 msec costs about $10k | ||
| + | |||
| + | ===Tungsten Disks=== | ||
| + | |||
| + | ;Dimensions are in cm | ||
| + | |||
| + | [[File:HRRL_PosTargetDesign_4-20-11.png| 200 px]] | ||
http://www.alibaba.com/product-gs/346924116/Tungsten_Disk_With_Screw.html | http://www.alibaba.com/product-gs/346924116/Tungsten_Disk_With_Screw.html | ||
| Line 168: | Line 306: | ||
http://www.cleveland-tungsten.com/ | http://www.cleveland-tungsten.com/ | ||
| − | ==Brushless Motor== | + | |
| + | If the motor has a radius of 2.5" and I want to shield the motor from the beam using 2" of Pb and the beam is about 1" in diameter then I want a Tungsten disk that is | ||
| + | |||
| + | 5.21" in radius = 13.25 cm in radius ~ 30 cm in diameter | ||
| + | |||
| + | Then density of Tungsten is | ||
| + | |||
| + | 19.25 g/cm^3 | ||
| + | |||
| + | |||
| + | 19.25 g/cm^3 \times \pi (30 cm)^2 = 54,428 g/cm | ||
| + | |||
| + | = 8.7 kg if it is 0.16 cm thick | ||
| + | |||
| + | The moment of inertia for a disk about its center is MR^2/2 | ||
| + | |||
| + | So I = 8.7kg \times (0.3 m)^2/2 = 0.4 kg m^2 | ||
| + | |||
| + | I should look into a ring of tungsten attached to a less dense material. | ||
| + | |||
| + | VX-U42 torque is about 50 in-lbs = 5.65 N m | ||
| + | |||
| + | Max acceleration would be | ||
| + | |||
| + | <math>\alpha = \frac{5.65 N m}{0.4 kg m^2} = 14.4 rad/sec \times \frac{1}{2 \pi} = 2.3 cycles/sec</math> | ||
| + | |||
| + | ===Brushless Motor=== | ||
| + | |||
| + | ====Motor wiring diagram==== | ||
| + | |||
| + | [[Media:U-42EmpireMagneticsMotorWiringDiag.pdf]] | ||
| + | |||
| + | |||
| + | Rick Halstead | ||
| + | |||
| + | 5830 Commerce Blvd | ||
| + | |||
| + | Rohnert Park, CA 94928 | ||
| + | |||
| + | Phone: 707-584-2801 | ||
| + | |||
| + | Fax: 707-584-3418 | ||
rick@empiremagnetics.com: | rick@empiremagnetics.com: | ||
| Line 178: | Line 357: | ||
We need 10^{-8 }Torr | We need 10^{-8 }Torr | ||
| − | ==Rotary coupler== | + | Vacuum lab grade motor U42. |
| + | |||
| + | http://www.empiremagnetics.com/prod_vac/prod_vac_vx_stepper_frame42.htm | ||
| + | |||
| + | |||
| + | Tony: Some of the couplings I had in mind: | ||
| + | http://www.sdp-si.com/estore/CoverPg/Couplings.htm | ||
| + | |||
| + | http://www.servometer.com/products/couplings/ | ||
| + | |||
| + | I'm thinking the coupler with adaptation of a compression seal. | ||
| + | http://www.jaecofs.com/stainless-steel-compression-fittings.html | ||
| + | |||
| + | The challenge will be to get them to make a version that can be sealed | ||
| + | at each end, technically it is feasible, it's an issue of engineering | ||
| + | resource to chase them down, get a quote then propose it to you, so | ||
| + | you can get funding. | ||
| + | |||
| + | ====Motor COntroller==== | ||
| + | |||
| + | |||
| + | Jason Brickner | ||
| + | Olympus Controls | ||
| + | Tel. 208.475.4670 | Email jbrickner@olympus-controls.com | ||
| + | |||
| + | ====Torque==== | ||
| + | |||
| + | The MRI rotary Unions require 2 in-oz of torque each | ||
| + | |||
| + | The U42 has a minimum static torque of 375 in-oz (1 Nm/8.851 oz-in) = 42.4 Nm | ||
| + | |||
| + | The Momentum of inertia of a thin disk about its axial axis is | ||
| + | |||
| + | :<math>MR^2/2</math> | ||
| + | |||
| + | Moment of Inertia of a ring: | ||
| + | |||
| + | :<math>MR^2</math> | ||
| + | |||
| + | The target will be a disk of Aluminum with an outer ring of tungsten. | ||
| + | |||
| + | <math>I_{\mbox{Al disk}} =M_{\mbox{Al}} R^2</math> | ||
| + | |||
| + | <math>M_{\mbox{Al}}= \rho \times V = 2.7 g/cm^3 (0.2 cm) \times \pi ( 9 in 2.54 cm/in)^2 =2.7 g/cm^3 0.2 cm \pi 523 cm^2 = 886 g</math> | ||
| + | |||
| + | <math>I_{\mbox{Al disk}} =886 g \times 523 cm^2 = 463423 g cm^2 \times (1 oz/28 g) (1 in/2.54 cm) (1in/2.54 cm) = 2565 oz-in^2 | ||
| + | </math> | ||
| + | |||
| + | <math>Torque = 42.4 Nm = I \alpha</math> | ||
| + | |||
| + | \alpha = 42.4 Nm/(0.04 kg m^2))=1060 rad/sec^2 | ||
| + | |||
| + | I_{\mbox{W}} = MR^2 = | ||
| + | |||
| + | |||
| + | <math>M_{\mbox{W ring}} = 19.25 g/cm^3 \times \pi ((30 cm)^2 - (28.5 cm)^2) = 5.3 kg = 11.7 lbs</math> | ||
| + | |||
| + | <math>I = 5.3 kg \times 29 cm^2 = 0.4457 kg m^2</math> | ||
| + | |||
| + | <math>I_{tot} = I_{\mbox{Al disk}} + I_{\mbox{W}} = (0.04 + 0.4457) kg m^2</math> | ||
| + | |||
| + | <math>\alpha = 42.4 Nm/(0.49 kg m^2) = 87 rad/s^2</math> | ||
| + | |||
| + | How much time to accelerate to 50 Hz = <math>50 *2 *\pi</math> rad/sec? | ||
| + | |||
| + | <math>\omega_f = \alpha t^2/2</math> | ||
| + | |||
| + | <math>t = \sqrt{\frac{2 \omega_f}{\alpha}} =\sqrt{\frac{2 50 8 2 *\pi}{87}} = 4.2</math> seconds | ||
| + | |||
| + | ===Rotary coupler/Union=== | ||
| + | |||
| + | ====ORNL rotating tungsten target==== | ||
| + | |||
| + | Full Name: Thomas J. McManamy | ||
| + | |||
| + | Email Address: mcmanamytj@ornl.gov | ||
| + | |||
| + | Phone Number: 865-576-0039 | ||
| + | |||
| + | Fax Number: 865-241-6909 | ||
| + | |||
| + | Postal Address: OAK RIDGE NATIONAL LABORATORY | ||
| + | |||
| + | PO BOX 2008 MS6476 | ||
| + | |||
| + | OAK RIDGE TN 37831-6476 | ||
| + | |||
| + | http://www.ornl.gov/info/reporter/no116/nov09_dw.htm#revolution | ||
| + | |||
| + | ====DSTI==== | ||
| + | |||
| + | http://www.dsti.com/products/?gclid=CPWEvP6ogagCFRs5gwod6SSXtA | ||
| + | |||
| + | Brett Villella | ||
| + | brett.villella@dsti.com | ||
| + | |||
| + | Dynamic Sealing Technologies, Inc. | ||
| + | |||
| + | 13829 Jay Street NW | ||
| + | |||
| + | Andover, MN 55304 | ||
| + | |||
| + | Direct: 763-404-8021 | ||
| + | |||
| + | Main: 763-786-3758 | ||
| + | Fax: 763-786-9674 | ||
| + | |||
| + | Web: www.dsti.com | ||
| + | |||
| + | Model: SPS-5510-R.A , a single pass rotary union, the input connector is 3/4" diameter as shown in the drawing below. | ||
| + | |||
| + | The minimum torque needed to rotate base on zero pressure is 4 in-lbs. | ||
| + | |||
| + | [[File:SinglePassRotaryUnionDSTi_v1.pdf]] | ||
| + | |||
| + | The target chamber design should be able to accommodate a 4" = 3.14+ 1" length in order to accept a rotary union which works at liquid nitrogen temperatures. The above single pass rotary union is good to -25F according to the company. | ||
| + | |||
| + | Place order for 2 with Michel @ 763-404-8024 | ||
| + | |||
| + | ====gat==== | ||
| + | |||
| + | The guy from Empiremagnetics says that the ferofluid used in the unions below becomes stiff at low temperatures causes too much load on the motors. | ||
| + | |||
| + | |||
| + | http://www.gat-mbh.de/index.php?page=rotovac-en&group=produkte-en:rotating_unions-en | ||
http://www.tengxuan.net/old/product.asp?Catalog=8 | http://www.tengxuan.net/old/product.asp?Catalog=8 | ||
| Line 185: | Line 488: | ||
http://www.rotarysystems.com/?gclid=CID4r6z22acCFQM6gwodoQVQ9w | http://www.rotarysystems.com/?gclid=CID4r6z22acCFQM6gwodoQVQ9w | ||
http://rotarysystems.com/series-006 | http://rotarysystems.com/series-006 | ||
| + | |||
| + | ===Motor Controller=== | ||
| + | |||
| + | http://www.centent.com/ | ||
=Target specifications= | =Target specifications= | ||
| − | |||
| − | + | The U42 motor has a 4.2 inch diameter. With a 2" Pb brick for shielding this would put the target radiu to at least (2.1 + 2 + 1) 5.1 inches. | |
| + | === Moment of Inertia=== | ||
| + | |||
| + | <math>I_{Disk} = \frac{1}{2} MR^2</math> | ||
| + | |||
| + | <math>I_{Hoop} = \frac{1}{2} M(R_1^2 +R_2^2)</math> | ||
| + | |||
| + | |||
| + | R= 32 cm = 12.6 inches. | ||
| + | |||
| + | ===Torque=== | ||
| + | |||
| + | ===Rotational Speed=== | ||
| + | ====Mechanical design==== | ||
| + | |||
| + | An Aluminum disk will be machined to have several Tungsten targets attached. | ||
| + | |||
| + | The disk has a radius of about 5.1 inches. The circumference will be 2 \pi r \approx 45 inches. If the targets are 1" wide with 1" gaps, then you will have about 20 targets. | ||
| + | |||
| + | |||
| + | If you rotate the target at 1 Hz then in one second you can hit 20 targets. This means your rep rate can be 20 Hz. | ||
| + | |||
| + | If you rotate the target at 50 Hz then your rep rate can be 1 kHz. | ||
| + | |||
| + | But since you will have 20 gaps (empty target positions) then you could run at 2 kHz. | ||
| + | |||
| + | So a target rotating 25 Hz can accept a rep rate of 1 kHz. | ||
| + | |||
| + | |||
| + | The HRRL easily runs at 300 Hz. For a target with 20 foils you would run the motor at 300/40 = 7.5 Hz. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ====Heat load==== | ||
You will need at least 2 holes in the Tungsten disk which you can use as an empty target. The Max pulse rate of the Linac is 1 kHz. So a 500 Hz motor would be the Max speed needed if you have 2 Windows. | You will need at least 2 holes in the Tungsten disk which you can use as an empty target. The Max pulse rate of the Linac is 1 kHz. So a 500 Hz motor would be the Max speed needed if you have 2 Windows. | ||
| − | How long can a 1.6 mm thick piece of Tungsten be in a 600 Watt heat source before melting. | + | How long can a 1.6 mm thick piece of Tungsten that has an area of 2.5" x 2.5" be in a 600 Watt heat source before melting. |
Specific Heat Capacity = <math> 130 \frac{J}{kg K}</math> | Specific Heat Capacity = <math> 130 \frac{J}{kg K}</math> | ||
| Line 204: | Line 546: | ||
density = 19.25<math>\frac{g}{cm^3}</math> | density = 19.25<math>\frac{g}{cm^3}</math> | ||
| − | Volume = <math>.16 cm | + | Volume = <math>(.16 cm)(2.5 cm)^2 = 1 cm^3</math> |
| − | Mass = <math> | + | Mass = <math>1 cm^2 \times 19.25 g/cm^3 = 19.25 g |
:<math>Q = C_m m \Delta T = 130 \frac{J}{kg K} \times 0.967 kg \times (3600-300 K) = 414843 J = 600 J/s *t </math> Watt = J/s | :<math>Q = C_m m \Delta T = 130 \frac{J}{kg K} \times 0.967 kg \times (3600-300 K) = 414843 J = 600 J/s *t </math> Watt = J/s | ||
| Line 236: | Line 578: | ||
:<math>\frac{Q}{t} = \frac{\kappa A \Delta T}{d}</math> | :<math>\frac{Q}{t} = \frac{\kappa A \Delta T}{d}</math> | ||
:<math>\kappa \equiv</math> Heat Conductivity | :<math>\kappa \equiv</math> Heat Conductivity | ||
| − | [[ | + | |
| + | |||
| + | ==Sadiq's Calculation == | ||
| + | |||
| + | Moment of inertia of a cylinder rotating in with z axis: | ||
| + | |||
| + | <math> I = \frac{m r^2}{2} = \frac{\rho \times V r^2}{2} = \frac{\rho \times \pi r^2 h \times r^2}{2} = \frac{\rho \pi r^4 h}{2} </math> | ||
| + | |||
| + | <math>\alpha = \frac{d w}{dt} = \frac{d^2\theta}{dt^2} = \frac{\tau}{I} </math> | ||
| + | |||
| + | <math> w = \frac{\tau}{I}t + w_0 </math> | ||
| + | |||
| + | <math> \theta = \frac{1}{2} \frac{\tau}{I} t^2 + w_0 t + \theta_0 </math> | ||
| + | |||
| + | Angular change due to acceleration is: | ||
| + | |||
| + | <math> \Delta \theta = \frac{1}{2} \frac{\tau}{I} t^2 + w_0 t + \theta_0 - ( w_0 t + \theta_0) = \frac{1}{2} \frac{\tau}{I} t^2 </math> | ||
| + | |||
| + | Position change at some distance R from the center is | ||
| + | |||
| + | <math> \Delta l = \Delta \theta R = \frac{1}{2} \frac{\tau}{I} t^2 R</math> | ||
| + | |||
| + | <math> \Delta l = \frac{1}{2} \frac{\tau}{I} t^2 R</math> | ||
| + | |||
| + | Assume we just have one disk, and we are looking for position change at the radius, r=R. We are also looking at the the position change after one revolution, t = T. | ||
| + | |||
| + | <math> \Delta l = \frac{1}{2} \frac{\tau}{\frac{\rho \pi r^4 h}{2}} T^2 r = \frac{\tau}{\rho \pi r^3 h} \frac{1}{f^2} </math> | ||
| + | |||
| + | <math> f^2 r^3 = \frac{\tau}{\rho \pi h} \frac{1}{\Delta l } </math> | ||
| + | |||
| + | or | ||
| + | |||
| + | <math>f^2 r^3 \Delta l = \frac{\tau}{\rho \pi h} </math> | ||
| + | |||
| + | === Rough Estimation === | ||
| + | |||
| + | 100 oz-in = 0.706154 N*m | ||
| + | |||
| + | <math> \tau = 400~oz-in = 2.82462~N*m </math> | ||
| + | |||
| + | <math> \rho_{Al} = 2.7 ~g~ cm^{-3} = 2.7 \times 10^3 ~kg~ m^{-3}</math> | ||
| + | |||
| + | We choose: | ||
| + | |||
| + | <math> h = 1~inch = 0.0254 ~m</math> | ||
| + | |||
| + | |||
| + | <math> \Delta l = \frac{1}{4}~inch = 0.00635 ~m</math> | ||
| + | |||
| + | <math> f^2 r^3 = \frac{2.82462~N*m}{(2.7 \times 10^3 ~kg~ m^{-3} )\times 3.14 \times (0.0254 ~m)} \times \frac{1}{0.00635 ~m } = 2.0656616 </math> | ||
| + | |||
| + | <math> f^2 r^3 = 2.0656616 </math> | ||
| + | |||
| + | |||
| + | <math> r^3 = \frac{2}{f^2} </math> | ||
| + | |||
| + | <math> r = ( \frac{2}{f^2} ) ^ {1/3}</math> | ||
| + | |||
| + | Which means: If out motor has a torque of <math> 400~oz-in </math>, and rotating a 1 inch thick cylindrical aluminium plate, to move a point outer edge of the plate, forward or backward, 1/4 inch in next revolution, the radius and frequency of the plate should satisfy: | ||
| + | |||
| + | <math> r^3 = \frac{2}{f^2} </math> | ||
| + | |||
| + | |||
| + | {| border="1" |cellpadding="20" cellspacing="0 | ||
| + | |- | ||
| + | |r (cm) || r (inch) || Circumference (in) || #tar (Number of 1-inch-targets can be mounted on the disk) || Rep rate (Hz) || | ||
| + | |- | ||
| + | | 43.1 || 17.0 || 106.56 || 53 || 5 || | ||
| + | |- | ||
| + | | 27.1 || 10.7 || 67.00 || 33 || 10 || | ||
| + | |- | ||
| + | | 17.2 || 6.8 || 42.53 || 21 || 20 || | ||
| + | |- | ||
| + | | 13.0 || 5.1 || 32.14 || 16 || 30 || | ||
| + | |- | ||
| + | | 10.8 || 4.3 || 26.70 || 23 || 40 || | ||
| + | |- | ||
| + | | 9.3 || 3.7 || 22.99 || 11 || 50 || | ||
| + | |- | ||
| + | | 8.2 || 3.2 || 20.27 || 10 || 60 || | ||
| + | |- | ||
| + | | 7.4 || 2.9 || 18.30 || 9 || 70 || | ||
| + | |- | ||
| + | | 6.8 || 2.6 || 16.81 || 8 || 80 || | ||
| + | |- | ||
| + | | 6.27 || 2.5 || 15.50 || 7 || 90 || | ||
| + | |- | ||
| + | | 5.85 || 2.2 || 14.46 || 7 || 100 || | ||
| + | |- | ||
| + | | 3.68 || 1.45 || 9.10 || 4 || 200 || | ||
| + | |- | ||
| + | | 2.81 || 1.11 || 6.95 || 3 || 300 || | ||
| + | |- | ||
| + | | 2.0 || 0.787 || 4.94 || 2 || 500 || | ||
| + | |- | ||
| + | | 1.25 || 0.492 || 3.09 || 1 || 1000 || | ||
| + | |||
| + | |} | ||
| + | |||
| + | ==Q== | ||
| + | Q: Does the W target has to be in the vacuum? | ||
| + | What if we have it in the air, at the ends of the beam line we have very thin vacuum window? | ||
| + | In photofission experiment we had 1 mil vacuum window. under | ||
| + | 15 MeV e- beam, only 1/1000 electron will interact with the window, produce bremsstrahlung photon. | ||
| + | |||
| + | Q: Can we make positron target that is inner part of the vacuum box, then we rotate all the box. Heat will be transfered to box, | ||
| + | box can cooled by water from outside. | ||
| + | May be box does not have to rotation movement? I can do other moments like up-down and right-left. | ||
| + | |||
| + | |||
| + | I think we can make a Tungsten target as a part of the beam line. That means outer part Tungsten target will be beam pine. | ||
| + | Then we can use water cooling to cool our Tungsten target from outside. | ||
| + | Before we had all the electrons hitting Faraday Cup, which did not melt the copper even when there was not cooling water | ||
| + | circling around FC. | ||
| + | Tungsten has higher melting point, plus we run cooling water around Tungsten target, then Tungsten shouldn't melt. | ||
| + | |||
| + | |||
| + | The first version of a positron converter target will be designed to distribute the heat load by rotating the tungsten target. | ||
| + | |||
| + | |||
| + | Calculate for 1 mm and 2 mm thick Tungsten | ||
| + | |||
| + | |||
| + | Look for Tungsten disks to attach to brushless motor and fit into beam pipe | ||
| + | |||
| + | |||
| + | = W Target = | ||
| + | |||
| + | W target at [http://www.alfa.com/en/gp100w.pgm?dsstk=13981 Tungsten foil, 1.0mm (0.04in) thick, 99.95% (metals basis)] | ||
| + | |||
| + | Pricing and Availability | ||
| + | Size ($) Price | ||
| + | 25x50mm 154.00 | ||
| + | 50x100mm 258.00 | ||
| + | |||
| + | |||
| + | |||
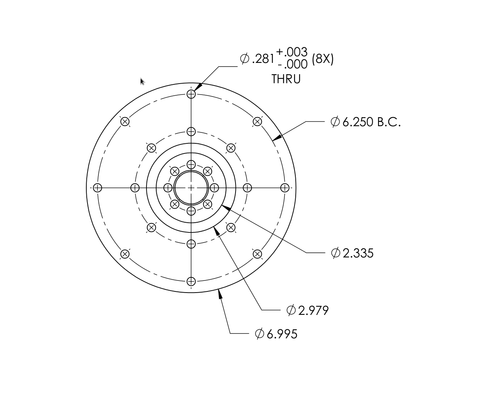
| + | Target Hub: [[File:W-Tar-Hub.png | 500 px]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | = Chamber = | ||
| + | |||
| + | Conceptual design to review: [[Media:hrrl_pos_ch_concept_des_8Aug2012.pdf]] | ||
| + | |||
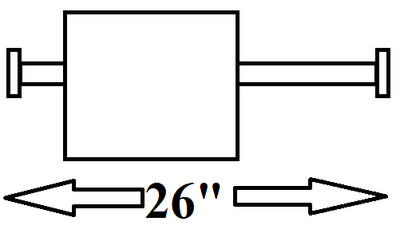
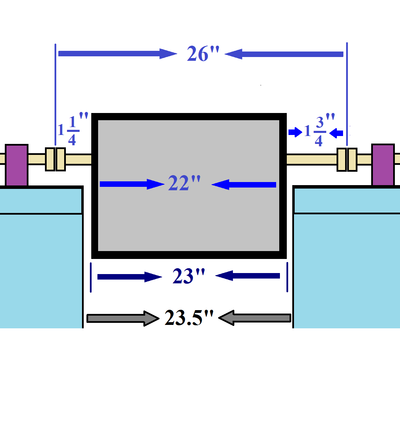
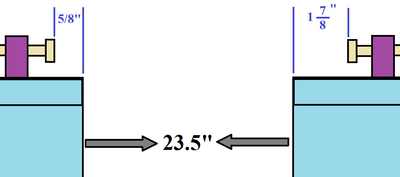
| + | [[File:hrrl_pos_ch_space_1.jpg | 400 px]] [[File:hrrl_pos_ch_space_2.jpg | 400 px]] | ||
| + | |||
| + | Chamber's flange to flange distance in Z direction should be 26 inches. The flange down stream the beamline should be as short as possible. | ||
| + | |||
| + | [[File:hrrl_pos_ch_space_3.png | 400 px]] | ||
| + | |||
| + | [[File:hrrl_pos_ch_space_4.png | 400 px]] | ||
| + | |||
| + | [[File:hrrl_pos_ch_space_5.png | 400 px]] | ||
| + | |||
| + | |||
| + | == Rotating target system length in Z == | ||
| + | |||
| + | The end to end distance of rotating target system with 2 elbows at two ends measured by Dr. Forest and Sadiq | ||
| + | |||
| + | Dr. Forest: 21.5 inches. | ||
| + | |||
| + | Sadiq: <math>21\frac{1}{8}~21\frac{3}{8}</math> inches. | ||
| + | |||
| + | |||
| + | |||
| + | == Chamber Target system == | ||
| + | |||
| + | [[File:HRRL_Cham_T1_sys_1.jpg | 400 px]] | ||
| + | [[File:HRRL_Cham_T1_sys_2.jpg | 400 px]] | ||
| + | |||
| + | Go Back [[Positrons]] | ||
Latest revision as of 22:26, 12 October 2012
PositronTargetWorkByChrissJackson
Target Construction
Current beam line distances for target to be inserted into
Motor
Empire Magnetics Model U42
- Wiring Diagram
- Media:U-42EmpireMagneticsMotorWiringDiag.pdf
Motor Controller
Power supply
STR8
STR8 Manuals:
Media:STR_Quick_Setup_Guide.pdf
Datasheet:
Media:STR_Brochure_925-0002_RevC.pdf
Design
Documents
File:BRACKET TUBE END SUPPORT 1.pdf
File:COOLING COOL A HELICAL.PDF
File:FITTING ASSY 1 ISO CUT AWAY 2.PDF
File:S VSRH U42 RTD 110726A SYSTEM LAYOUT.pdf
45 degree angle
The Tungsten target should make a 45 degree angle with the beam.
make the motor so it can be rotated.
Beam Heat Load
- Accelerator Settings
| beam energy | 10 MeV |
| Rep Rate: | 300 Hz |
| I_peak: | 200 mA/pulse |
| pulse width: | 0.1 s (100 ns) |
| Vacuum: | Torr |
Time on for one second is 30 us. and Time off is 0.999999 s The average current 0.999999 * 0 + 0.000001*300*200mA = 60A.
P = (10 MeV) (60 A) = 600 Watts.
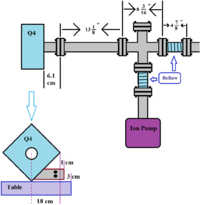
Target Chamber design
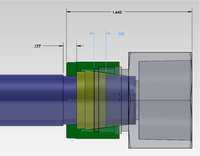
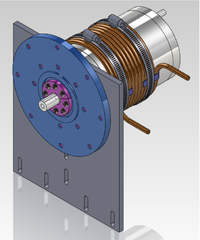
Latest Design From empire and Sadiq's measurement of the available space
 |
 |
 |
|
| Target motor Design | Available beam line space | Motor axle coupling to rotary union | Hub and spline to attache targets |
- Dimensions are in inches
There is an 18" space in Z for the target chamber. If you want to rotate a disk on the 5" wide motor you will need at least a a 10" x 10" area.
So we could try as a first design a chamber which is 18" x 15" x 15". We need the following
- 2 beam flanges flush with the walls of the chamber.
- 2 flanges to allow access for hands to work on the target motor inside. It should able to fit hands through.
- a flange on top which will allow a 10" diameter target disk to come out.
- a flange on the bottom for the ion pump.
July Design From empire
 |

|
| Rotary Union overlayed on conceptual drawing. | Conceptual drawing of stator cooling lines. We will need separate connection to them on the vacuum chamber. |
Gate Valve - Target distance
The distance from the front of the gate valve to the most beam upstream part of the target chamber is
88.43 cm
The gate valve closes in 0.7 sec.
So water would need to travel at a speed of 88.43 cm/0.7 sec = 1.26 m/sec
Properties of Tungsten
- Melting Point = 3695 K.
- Heat Capacity =
- These data are from: Tungsten
- Heat loss due to radiation: ( \sigma T^4)
Tungsten Temperature as a function of heat load
- IAC beamline pressure = Torr
- The Tungsten heats up when an MeV energy electron impinges its surface. The imperfect vacuum inside the beam pipe does allow some radiative cooling.
- Conduction and Radiation
Calculating Radiators Equilibrium Temperature
1.Calculating number of particles per second
We have electron beam of:
Frequency: f=1000Hz
Peak current: I=10~mAmp=0.01 Amp
Pulse width: seconds
So, how many electrons we have in each second?
By Q=It, we have
Where N is the total electron numbers hits target per second, e is electron charge and f, I and ∆t are given above. Number of particle per second is:
2.Calculating Energy deposited per second
If we find the energy deposited by each electron and multiply to the total number of electrons in each second, we will find the total energy per second deposited in radiator.
To find energy deposited by each electron, we need to use formula
Where is is energy deposited by one electron, is mean energy loss (also stopping power) by collision of electron and is thickness of the radiator.
Actually, energy loss of a electron comes from two parts: 1) the emission of electromagnetic radiation arising from scattering in the electric field of a nucleus (bremsstrahlung); 2) Collisional energy loss when passing through matter. Bremsstrahlung will not contribute to the temperature, because it is radiation.
Stopping power can be found from nuclear data tables and thickness is 0.001 times of radiation length. From Particle Data group we got radiation length and average total stopping powers around 15MeV for electrons in these materials from National Institute of Standards and Technology: Tungsten Stopping Power.
Table of Radiation Lengths
Note:These data is from Particle Data group,Link: [1].
| Elements | Radiation Lengths |
| W | 6.76 |
Table of energy calculations
For the thickness of 0.001 Radiation Length (0.0001RL) of radiators. Note: is from National Institute of Standards and Technology. Link: [[2]])
| Elements | ) | (MeV) | (MeV/s) | (J/s) | |
| W | 1.247 | 0.00676 | 0.00842972 |
In above table,we took the total numbers of electrons per second and multiply it to Energy deposited by one electron,get total energy deposited per second (which is power).
3.Calculating equilibrium temperature using Stefan–Boltzmann law
If we assume that there is no energy conduction and total energy is just radiated from two surfaces of the radiators which are as big as beam spot,in our case beam spot is 2mm in diameter. According to Stefan–Boltzmann law, this total power radiated will be
Where T is radiating temperature P is the radiating power, A is surface area that beam incident and σ is Stefan–Boltzmann constant or Stefan's constant. To reach equilibrium temperature, Power deposited in and power radiated should be. So
so
Vendors
MDC Target Chamber
Target chamber: MDC vacuum products can send a prefab one you just need to weld up.
John Brooks
jbrooks@mdcvacuum.com
1-800-443-8817
or
510-265-3569
File:TargetChamberDesign 1.0.pdf
Tom Bogden (John's boss)
MDC does not have a fast closing gate valve. Model GV1500 closes in 0.7 seconds and costs $1600. One that closes in 10 msec costs about $10k
Tungsten Disks
- Dimensions are in cm
http://www.alibaba.com/product-gs/346924116/Tungsten_Disk_With_Screw.html
http://www.zlxtech.com.cn/products.asp?productcode=7401000404
http://www.cleveland-tungsten.com/
If the motor has a radius of 2.5" and I want to shield the motor from the beam using 2" of Pb and the beam is about 1" in diameter then I want a Tungsten disk that is
5.21" in radius = 13.25 cm in radius ~ 30 cm in diameter
Then density of Tungsten is
19.25 g/cm^3
19.25 g/cm^3 \times \pi (30 cm)^2 = 54,428 g/cm
= 8.7 kg if it is 0.16 cm thick
The moment of inertia for a disk about its center is MR^2/2
So I = 8.7kg \times (0.3 m)^2/2 = 0.4 kg m^2
I should look into a ring of tungsten attached to a less dense material.
VX-U42 torque is about 50 in-lbs = 5.65 N m
Max acceleration would be
Brushless Motor
Motor wiring diagram
Media:U-42EmpireMagneticsMotorWiringDiag.pdf
Rick Halstead
5830 Commerce Blvd
Rohnert Park, CA 94928
Phone: 707-584-2801
Fax: 707-584-3418
rick@empiremagnetics.com:
The VX grade motors, with dry lubes have been used in deep space (Wake Shield Module) where I'm told they were trying to get 10^-12 torr.
We need 10^{-8 }Torr
Vacuum lab grade motor U42.
http://www.empiremagnetics.com/prod_vac/prod_vac_vx_stepper_frame42.htm
Tony: Some of the couplings I had in mind:
http://www.sdp-si.com/estore/CoverPg/Couplings.htm
http://www.servometer.com/products/couplings/
I'm thinking the coupler with adaptation of a compression seal. http://www.jaecofs.com/stainless-steel-compression-fittings.html
The challenge will be to get them to make a version that can be sealed at each end, technically it is feasible, it's an issue of engineering resource to chase them down, get a quote then propose it to you, so you can get funding.
Motor COntroller
Jason Brickner Olympus Controls Tel. 208.475.4670 | Email jbrickner@olympus-controls.com
Torque
The MRI rotary Unions require 2 in-oz of torque each
The U42 has a minimum static torque of 375 in-oz (1 Nm/8.851 oz-in) = 42.4 Nm
The Momentum of inertia of a thin disk about its axial axis is
Moment of Inertia of a ring:
The target will be a disk of Aluminum with an outer ring of tungsten.
\alpha = 42.4 Nm/(0.04 kg m^2))=1060 rad/sec^2
I_{\mbox{W}} = MR^2 =
How much time to accelerate to 50 Hz = rad/sec?
seconds
Rotary coupler/Union
ORNL rotating tungsten target
Full Name: Thomas J. McManamy
Email Address: mcmanamytj@ornl.gov
Phone Number: 865-576-0039
Fax Number: 865-241-6909
Postal Address: OAK RIDGE NATIONAL LABORATORY
PO BOX 2008 MS6476
OAK RIDGE TN 37831-6476
http://www.ornl.gov/info/reporter/no116/nov09_dw.htm#revolution
DSTI
http://www.dsti.com/products/?gclid=CPWEvP6ogagCFRs5gwod6SSXtA
Brett Villella brett.villella@dsti.com
Dynamic Sealing Technologies, Inc.
13829 Jay Street NW
Andover, MN 55304
Direct: 763-404-8021
Main: 763-786-3758
Fax: 763-786-9674
Web: www.dsti.com
Model: SPS-5510-R.A , a single pass rotary union, the input connector is 3/4" diameter as shown in the drawing below.
The minimum torque needed to rotate base on zero pressure is 4 in-lbs.
File:SinglePassRotaryUnionDSTi v1.pdf
The target chamber design should be able to accommodate a 4" = 3.14+ 1" length in order to accept a rotary union which works at liquid nitrogen temperatures. The above single pass rotary union is good to -25F according to the company.
Place order for 2 with Michel @ 763-404-8024
gat
The guy from Empiremagnetics says that the ferofluid used in the unions below becomes stiff at low temperatures causes too much load on the motors.
http://www.gat-mbh.de/index.php?page=rotovac-en&group=produkte-en:rotating_unions-en
http://www.tengxuan.net/old/product.asp?Catalog=8
http://www.rotarysystems.com/?gclid=CID4r6z22acCFQM6gwodoQVQ9w
http://rotarysystems.com/series-006
Motor Controller
Target specifications
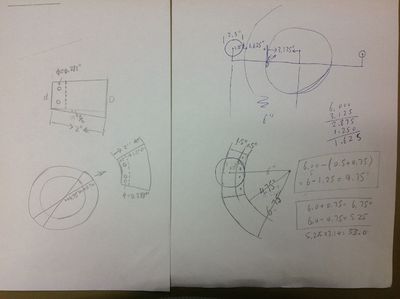
The U42 motor has a 4.2 inch diameter. With a 2" Pb brick for shielding this would put the target radiu to at least (2.1 + 2 + 1) 5.1 inches.
Moment of Inertia
R= 32 cm = 12.6 inches.
Torque
Rotational Speed
Mechanical design
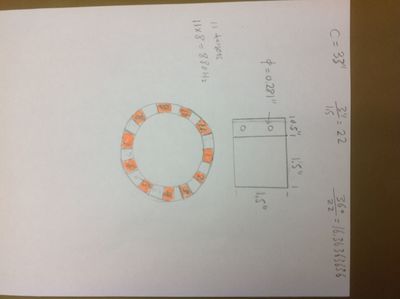
An Aluminum disk will be machined to have several Tungsten targets attached.
The disk has a radius of about 5.1 inches. The circumference will be 2 \pi r \approx 45 inches. If the targets are 1" wide with 1" gaps, then you will have about 20 targets.
If you rotate the target at 1 Hz then in one second you can hit 20 targets. This means your rep rate can be 20 Hz.
If you rotate the target at 50 Hz then your rep rate can be 1 kHz.
But since you will have 20 gaps (empty target positions) then you could run at 2 kHz.
So a target rotating 25 Hz can accept a rep rate of 1 kHz.
The HRRL easily runs at 300 Hz. For a target with 20 foils you would run the motor at 300/40 = 7.5 Hz.
Heat load
You will need at least 2 holes in the Tungsten disk which you can use as an empty target. The Max pulse rate of the Linac is 1 kHz. So a 500 Hz motor would be the Max speed needed if you have 2 Windows.
How long can a 1.6 mm thick piece of Tungsten that has an area of 2.5" x 2.5" be in a 600 Watt heat source before melting.
Specific Heat Capacity =
Thermal Conductivity =
The Melting point of Tungsten is 3600 Kelvin.
density = 19.25
Volume =
Mass = Watt = J/s
If Zinc
- C_m = 0.39 J/g/K Density = 7.13 g/cm^3 \Right arrow M = 7.13 \times 50.3 = 358 g, Melting point 693 K
- Q = 0.39 \times 0.358 \times 393 = 55 Joules = 10^3 Watts * t \Rightarrow t = 0.055 s \Rightarrow 18 Hz.
Now You need to calculate how quickly water can absorb heat
- Water properties
- C_m = 4.12 J/g/K , Density = 1 g/cm^3 assuming aflow rate of 1 liter/sec \Rightarrow mass = 1 g, Boiling point water = 373.15
Tungsten's specific heat capacity is about 30 times larger than water. So for the same mass and power input water's temperature will change a factor of 30 more than tungsten.
In 1 second Tungsten's temperature change will be
- \frac{600 J}{130 \times 0.967} = 5K
Copper coils which have water flowing through them are soldered to the Tungsten. The water is a heat sink transferring heat from the Tungsten to the water.
- Heat transfer by conduction
- Heat Conductivity
Sadiq's Calculation
Moment of inertia of a cylinder rotating in with z axis:
Angular change due to acceleration is:
Position change at some distance R from the center is
Assume we just have one disk, and we are looking for position change at the radius, r=R. We are also looking at the the position change after one revolution, t = T.
or
Rough Estimation
100 oz-in = 0.706154 N*m
We choose:
Which means: If out motor has a torque of , and rotating a 1 inch thick cylindrical aluminium plate, to move a point outer edge of the plate, forward or backward, 1/4 inch in next revolution, the radius and frequency of the plate should satisfy:
| r (cm) | r (inch) | Circumference (in) | #tar (Number of 1-inch-targets can be mounted on the disk) | Rep rate (Hz) | |
| 43.1 | 17.0 | 106.56 | 53 | 5 | |
| 27.1 | 10.7 | 67.00 | 33 | 10 | |
| 17.2 | 6.8 | 42.53 | 21 | 20 | |
| 13.0 | 5.1 | 32.14 | 16 | 30 | |
| 10.8 | 4.3 | 26.70 | 23 | 40 | |
| 9.3 | 3.7 | 22.99 | 11 | 50 | |
| 8.2 | 3.2 | 20.27 | 10 | 60 | |
| 7.4 | 2.9 | 18.30 | 9 | 70 | |
| 6.8 | 2.6 | 16.81 | 8 | 80 | |
| 6.27 | 2.5 | 15.50 | 7 | 90 | |
| 5.85 | 2.2 | 14.46 | 7 | 100 | |
| 3.68 | 1.45 | 9.10 | 4 | 200 | |
| 2.81 | 1.11 | 6.95 | 3 | 300 | |
| 2.0 | 0.787 | 4.94 | 2 | 500 | |
| 1.25 | 0.492 | 3.09 | 1 | 1000 |
Q
Q: Does the W target has to be in the vacuum? What if we have it in the air, at the ends of the beam line we have very thin vacuum window? In photofission experiment we had 1 mil vacuum window. under 15 MeV e- beam, only 1/1000 electron will interact with the window, produce bremsstrahlung photon.
Q: Can we make positron target that is inner part of the vacuum box, then we rotate all the box. Heat will be transfered to box, box can cooled by water from outside. May be box does not have to rotation movement? I can do other moments like up-down and right-left.
I think we can make a Tungsten target as a part of the beam line. That means outer part Tungsten target will be beam pine. Then we can use water cooling to cool our Tungsten target from outside. Before we had all the electrons hitting Faraday Cup, which did not melt the copper even when there was not cooling water circling around FC. Tungsten has higher melting point, plus we run cooling water around Tungsten target, then Tungsten shouldn't melt.
The first version of a positron converter target will be designed to distribute the heat load by rotating the tungsten target.
Calculate for 1 mm and 2 mm thick Tungsten
Look for Tungsten disks to attach to brushless motor and fit into beam pipe
W Target
W target at Tungsten foil, 1.0mm (0.04in) thick, 99.95% (metals basis)
Pricing and Availability Size ($) Price 25x50mm 154.00 50x100mm 258.00
Chamber
Conceptual design to review: Media:hrrl_pos_ch_concept_des_8Aug2012.pdf
Chamber's flange to flange distance in Z direction should be 26 inches. The flange down stream the beamline should be as short as possible.
Rotating target system length in Z
The end to end distance of rotating target system with 2 elbows at two ends measured by Dr. Forest and Sadiq
Dr. Forest: 21.5 inches.
Sadiq: inches.
Chamber Target system
Go Back Positrons