Difference between revisions of "EG1 Teleconferences DeltaDoverD"
| (26 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | =2/26/09= | ||
| + | |||
| + | |||
| + | [http://www.jlab.org/Hall-B/secure/eg1/EG2000/nevzat/UPGRADE_DST/cuts/OSICuts.h OSICuts] | ||
| + | |||
=2/12/09= | =2/12/09= | ||
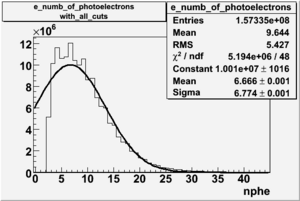
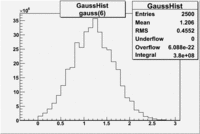
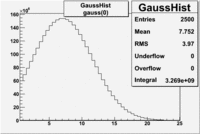
| − | An estimate of the pion contamination in the electron candidates from the 5 GeV data set appears below. Cuts are applied on the electron candidates based on the ratio of the energy deposited by the electron candidate in the electron calorimeter to the particles momentum measured by track reconstruction using hits in the drift chamber | + | An estimate of the pion contamination in the electron candidates from the 5 GeV data set appears below. Cuts are applied on the electron candidates based on the ratio of the energy deposited by the electron candidate in the electron calorimeter to the particles momentum measured by track reconstruction using hits in the drift chamber <math>\left ( \frac{E}{p} \right )</math>. |
As reported at the last teleconference on 1/20/09, these cuts were taken from [[Media:Yelena_Prok_Measurement_of_The_Spin_structure_Function_of_The_Proton_in_The_Resonance_Region_Thesis.pdf]] | As reported at the last teleconference on 1/20/09, these cuts were taken from [[Media:Yelena_Prok_Measurement_of_The_Spin_structure_Function_of_The_Proton_in_The_Resonance_Region_Thesis.pdf]] | ||
| − | and applied to the 5 GeV data sample. The number of photoelectrons measured by the cherenkov detector is shown below. The goal is to | + | and applied to the 5 GeV data sample. The number of photoelectrons measured by the cherenkov detector is shown below. The goal is to estimate the number of pions which contaminate the electron candidate sample. This is done |
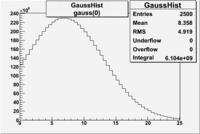
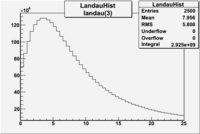
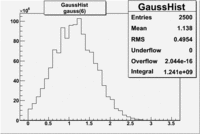
by fitting the photoelectron distribution to 2 gaussian distributions and a Landau distribution. Integrals of the fits over the region of interest are used to determine the pion contamination to the electron candidates. | by fitting the photoelectron distribution to 2 gaussian distributions and a Landau distribution. Integrals of the fits over the region of interest are used to determine the pion contamination to the electron candidates. | ||
| Line 48: | Line 53: | ||
Electrons in the sample(using all cuts except nphe>2.5) =<br> | Electrons in the sample(using all cuts except nphe>2.5) =<br> | ||
<math> = \frac {Integral(gauss(0))}{Integral(gauss(0) + landau(3) + gauss(6))} =</math><br> | <math> = \frac {Integral(gauss(0))}{Integral(gauss(0) + landau(3) + gauss(6))} =</math><br> | ||
| − | <math> = \frac{6.104 \times 10^9}{ 6.104 \times 10^9 + 2.925 \times 10^9 + 1.241 \times 10^9} = </math> <br> | + | <math> = \frac{6.104 \times 10^9 + 2.925 \times 10^9}{ 6.104 \times 10^9 + 2.925 \times 10^9 + 1.241 \times 10^9} = </math> <br> |
| − | <math> = | + | <math> = 87 % </math><br> |
| Line 58: | Line 63: | ||
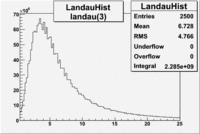
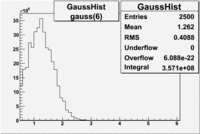
Electrons in the sample(including nphe>2.5 cut) =<br> | Electrons in the sample(including nphe>2.5 cut) =<br> | ||
<math> = \frac {Integral(gauss(0))}{Integral(gauss(0) + landau(3) + gauss(6))} =</math><br> | <math> = \frac {Integral(gauss(0))}{Integral(gauss(0) + landau(3) + gauss(6))} =</math><br> | ||
| − | <math> = \frac{5.367 \times 10^9}{ 5.367 \times 10^9 + 2.434 \times 10^9 + 4.928 \times 10^6} = </math> <br> | + | <math> = \frac{5.367 \times 10^9 + 2.434 \times 10^9}{ 5.367 \times 10^9 + 2.434 \times 10^9 + 4.928 \times 10^6} = </math> <br> |
| − | <math> = | + | <math> = 99.9 % </math><br> |
;Conclusion: Using only EC cuts, electrons in the sample are 60 %, after using the cut on the number of photoelectrons the pion contamination decreased and 69 % of the particles are electrons, that means pion contamination is 31 %. It decreased by 9 %. | ;Conclusion: Using only EC cuts, electrons in the sample are 60 %, after using the cut on the number of photoelectrons the pion contamination decreased and 69 % of the particles are electrons, that means pion contamination is 31 %. It decreased by 9 %. | ||
| + | If we assume that the photoelectrons from electrons are described by the Gaussian and landau distribution and that the pions are only in the gaussian distribution then | ||
| + | we would expect our electron candidates to have a pion contamination of <math>\frac{4.928 \times 10^6}{5.367 \times 10^9 + 2.434 \times 10^9 } \times 100 %= 0.06 %</math>. | ||
;For Pions | ;For Pions | ||
| − | In this case, Josh's pion cut code was used. The number of entries decreased by ~ | + | In this case, Josh's pion cut code was used. The number of entries decreased by ~ 20 %. |
{| border="1" |cellpadding="20" cellspacing="0 | {| border="1" |cellpadding="20" cellspacing="0 | ||
| Line 104: | Line 111: | ||
| || colspan="3" align="center"| without cuts || colspan="3" align="center" | with cuts(<math>EC_{inner}/P>0.06</math>, <math>EC_{tot}/P>0.24</math>, e_momentum>3 GeV) | | || colspan="3" align="center"| without cuts || colspan="3" align="center" | with cuts(<math>EC_{inner}/P>0.06</math>, <math>EC_{tot}/P>0.24</math>, e_momentum>3 GeV) | ||
|- | |- | ||
| − | | gauss(0)|| p0= | + | | gauss(0)|| p0=8.788e+06 +\-12717 || p1=6.139 +\-0.01 || p2=5.824 +\-0.004 || p0=3.087e+06 +\-1393 || p1=7.038 +\-0.002 || p2=4.573 +\-0.001 |
|- | |- | ||
| − | | landau(3)|| p3=3.872e+07 +\- | + | | landau(3)|| p3=3.872e+07 +\- 112058 || p4=3.19 +\-0.01 || p5=2.488 +\-0.003 || p3=1.774e+07 +\-12968 || p4=3.797 +\-0.002 || p5=1.398 +\-0.001 |
|- | |- | ||
| − | | gauss(6)|| p6=2.727e+07 +\- | + | | gauss(6)|| p6=2.727e+07 +\- 8869 || p7=1.094 +\- 0.000 ||p8= 0.5347 +\- 0.0002 || p6=3.285e+06 +\-3512 || p7=1.198 +\-0.000 || p8= -0.4637 +\-0.0005 |
|}<br> | |}<br> | ||
| Line 130: | Line 137: | ||
<math> = 55 % </math><br> | <math> = 55 % </math><br> | ||
| + | ;Conclusion: The pion contamination is this case is the same as it was before using the cut nphe>0.5 cut. The pion contamination is 45 % in the sample. | ||
| + | If we assume that the photoelectrons from electrons are described by the Gaussian and landau distribution and that the pions are only in the gaussian distribution then | ||
| + | we would expect our electron candidates to have a pion contamination of <math>\frac{3.571 \times 10^8}{3.269 \times 10^9 + 2.285 \times 10^9 } \times 100 %= 0.06 %</math>. | ||
;For Pions | ;For Pions | ||
| − | In this case, Josh's pion cut code was used. The number of entries decreased by ~ | + | In this case, Josh's pion cut code was used. The number of entries decreased by ~ 20 % . |
{| border="1" |cellpadding="20" cellspacing="0 | {| border="1" |cellpadding="20" cellspacing="0 | ||
| Line 142: | Line 152: | ||
;For Electrons | ;For Electrons | ||
In order to remove the peak around ~ 1.5 PE and some high energy pions which have enough energy to cause the Cherenkov radiation the cut on nphe was applied. | In order to remove the peak around ~ 1.5 PE and some high energy pions which have enough energy to cause the Cherenkov radiation the cut on nphe was applied. | ||
| − | The number of entries after applying the following cuts - <math>EC_{inner}/P>0. | + | The number of entries after applying the following cuts - <math>EC_{inner}/P>0.06</math> <math>EC_{tot}/P>0.24</math>, e_momentum > 3 GeV and nphe > 0.5 decreased by 73 %. |
{| border="1" |cellpadding="20" cellspacing="0 | {| border="1" |cellpadding="20" cellspacing="0 | ||
| Line 148: | Line 158: | ||
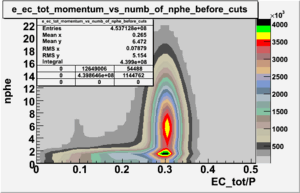
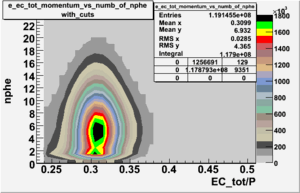
|[[Image:EC_tot_P_vs_nphe_for_electrons_all_data_without_cuts_2_1.gif|300px|thumb| <math>EC_{tot}</math>/P vs nphe for electrons without cuts]] || [[Image:EC_tot_P_vs_nphe_for_electrons_all_data_with_cuts_2_1.gif|300px|thumb| <math>EC_{tot}</math>/P vs nphe for electrons after cuts on <math>EC_{tot}/P</math>, <math>EC_{inner}/P</math>, e_momentum and nphe]] | |[[Image:EC_tot_P_vs_nphe_for_electrons_all_data_without_cuts_2_1.gif|300px|thumb| <math>EC_{tot}</math>/P vs nphe for electrons without cuts]] || [[Image:EC_tot_P_vs_nphe_for_electrons_all_data_with_cuts_2_1.gif|300px|thumb| <math>EC_{tot}</math>/P vs nphe for electrons after cuts on <math>EC_{tot}/P</math>, <math>EC_{inner}/P</math>, e_momentum and nphe]] | ||
|} | |} | ||
| + | |||
| + | |||
| + | Repeat the above calculation using Nevzat's cuts. | ||
| + | http://www.jlab.org/Hall-B/secure/eg1/EG2000/nevzat/GEOM_CC_CUTS/ | ||
=1/29/09= | =1/29/09= | ||
| Line 176: | Line 190: | ||
;PE Fit equation (Osipenko's CLAS Note 2004-20 [[Image:CLAS_Note-2004-020.pdf]]) | ;PE Fit equation (Osipenko's CLAS Note 2004-20 [[Image:CLAS_Note-2004-020.pdf]]) | ||
;<math>N_{pe}= p_0 e^{-0.5 \left (\frac{x-p_1}{p_2} \right )^2} + p4\frac{1}{1-\left(\frac{x-p5}{p6}\right )} + p_6 e^{-0.5 \left (\frac{x-p_7}{p_8} \right )^2}</math> | ;<math>N_{pe}= p_0 e^{-0.5 \left (\frac{x-p_1}{p_2} \right )^2} + p4\frac{1}{1-\left(\frac{x-p5}{p6}\right )} + p_6 e^{-0.5 \left (\frac{x-p_7}{p_8} \right )^2}</math> | ||
| + | |||
| + | |||
| + | <pre> | ||
| + | The CLAS note above says 2 Poisson convolution by a gaussian are used to fit NPE histogram. | ||
| + | The Poisson distribution starts to look like a gaussian when the Poisson mean value is larger | ||
| + | than 4. Our electron candidates theoretically have NPE = 13 and pions have NPE>4 when the | ||
| + | pion energies are above 3 GeV. | ||
| + | |||
| + | We seem to get good fits if we use 2 Gaussians convoluted with a Landau. | ||
| + | |||
| + | </pre> | ||
As we will show below, the first peak is due to the misidentification of a negative pion as an electron. | As we will show below, the first peak is due to the misidentification of a negative pion as an electron. | ||
| Line 255: | Line 280: | ||
| + | =21-07-2010= | ||
| + | |||
| + | ==Cuts== | ||
| + | |||
| + | The correct identification of an electron and a pion is the main requirement for a semi-inclusive analysis. unfortunately, the pion is able to generate cerenkov radiation an as a result be misidentified as an electron. This contamination of the electron sample is removed using the cuts on the energy deposited in the electromagnetic calorimeter, the number of photoelectrons in the Cherenkov counter and fiducial cuts on the detector acceptance. | ||
| + | The energy deposition in the calorimeter for electrons and pions is different. Pions are minimum ionizing charge particles depositing into the calorimeter which is independent of the pion's momentum once the momentum is above ~ 0.08 GeV. On the other hand, electrons produce photoelectrons and create electromagnetic shower releasing the energy into the calorimeter which is proportional to their momentum. In order to remove contamination due to the energy deposition in the calorimeter the following cut was introduced: <math>EC_{total}>0.2*p</math>. The cut was also applied to the energy collected in the inner part of the calorimeter: <math>EC_{inner}>0.06*p</math> , because the ratio of the energy deposited in the total to the inner calorimeter depends on the thickness of the detector and is a constant.<br> | ||
| + | [[Image:e_total_vs_e_inner1_before_cuts_file_dst27070.gif|200px]][[Image:e_total_vs_e_inner1_after_cuts_file_dst27070.gif|200px]]<br> | ||
| + | In addition to the cut on the energy deposited into the electromagnetic calorimeter, the misidentified electrons were excluded requiring a signal in the threshold CLAS Cherenkov detector. Pion's misidentified as electrons have been shown to produce around ~1.5 photoelectons in the cherenkov detector, as shown below. Geometrical cuts on the location of the particle at the entrance to the cerenkov detector were applied to reduce the pion contamination. The second histogram below shows that after cuts the peak around 1.5 is substantially reduced. <br> | ||
| + | {| border="1" |cellpadding="20" cellspacing="0 | ||
| + | |- | ||
| + | | No cuts || OSI Cuts | ||
| + | |- | ||
| + | | [[Image:electrons_nphe_without_cuts_all_data_with_fits.gif|200px|thumb|The number of photoelectrons without cuts]] || [[Image:electrons_nphe_with_OSIcuts_all_data_with_fits.gif|200px|thumb|The number of photoelectrons with OSI cuts]] | ||
| + | |} | ||
| + | |||
| + | ==phi_angle_in_CM_Frame_vs_Relative_Rate== | ||
| + | |||
| + | Because of wide range of kinematics, <math>{\varphi_{\pi}}^*</math> was measured only for certain lepton scattering <math>\theta_e</math> angles and invariant mass (W). Applying above described cuts: EC_inner>0.06, EC_tot/p>0.2, nphe>2.5 and <math>0.9<M_x<1.1</math>, for the following invariant mass <math>1.44<W<1.46</math> and <math>0.4<cos\theta_{pion}^{CM}<0.6</math> the <math>{\varphi_{\pi}}^*</math> vs relative rate distribution is shown below on the graph and compared with E99-107 data, which by itself is in agreement with the models.<br> | ||
| + | {| border="0" style="background:transparent;" align="center" | ||
| + | |- | ||
| + | | | ||
| + | [[Image:phi_angle_in_CM_Frame_vs_Relative_Rate_cos_theta_0-4_0-6_W_1-45.jpg|400px|thumb|<math>{\varphi_{\pi}}^*</math> vs Relative rate for fixed <math>cos\theta_{pion}^{CM}=0.5</math> and <math>W=1.45 GeV</math> <ref name="Park2008" > Bogus text</ref> <ref> http://clasweb.jlab.org/cgi-bin/clasdb/msm.cgi?eid=14&mid=16&data=on </ref> ]] | ||
| + | |}<br> | ||
| + | |||
| + | The EG1b data for kinematics chosen above show the same shape as E99-107 data. | ||
| + | |||
| + | |||
| + | '''If you follow the link below, you can find the comparison for the wide range of kinematics:''' | ||
| + | |||
| + | [[Phi_angle_in_CM_frame_for_different_runs]] | ||
| + | |||
| + | ==Electron Efficiency Ratio== | ||
| + | |||
| + | Used NH3 target runs with positive and negative torus. EC , nphe and OSI cuts are applied. Only electron was required. | ||
| + | |||
| + | {| border="1" |cellpadding="20" cellspacing="0 | ||
| + | |- | ||
| + | | File number || electron || electron | ||
| + | |- | ||
| + | | B<0 || [[File:electron26990_4.gif|200px]] || [[File:electron26990_5.gif|200px]] | ||
| + | |- | ||
| + | | B>0 || [[File:electron27113_4.gif|200px]] || [[File:electron27113_5.gif|200px]] | ||
| + | |} | ||
| + | |||
| + | |||
| + | Below is the graph of electron efficiency ratio when electron_paddle_number=7 for positive torus(Bp) and electron_paddle_number=11 for negative torus(B_n) | ||
| + | |||
| + | [[File:electronefficiencyratioBp7Bn11.jpg|300px]] | ||
| + | |||
| + | [[Media:electronefficiencyratioBp7Bn11.txt]] | ||
| + | |||
| + | |||
| + | In this case we required positive pion and electron and applied cut on <math>Q^2</math>(<math>1.05<Q^2<1.15</math>) | ||
| + | |||
| + | {|border="5" | ||
| + | !X_bj ||B_n/B_p Rates | ||
| + | |- | ||
| + | | 0.14 || 0.25 <math>\pm</math> 0.55 | ||
| + | |- | ||
| + | | 0.15 || 0.74 <math>\pm</math> 0.27 | ||
| + | |- | ||
| + | | 0.17 || 1.07 <math>\pm</math> 0.18 | ||
| + | |- | ||
| + | | 0.19 || 1.3 <math>\pm</math> 0.13 | ||
| + | |- | ||
| + | | 0.2 || 1.4 <math>\pm</math> 0.14 | ||
| + | |} | ||
[http://wiki.iac.isu.edu/index.php/EG1 Go Back] [[EG1]] | [http://wiki.iac.isu.edu/index.php/EG1 Go Back] [[EG1]] | ||
Latest revision as of 05:50, 21 July 2010
2/26/09
2/12/09
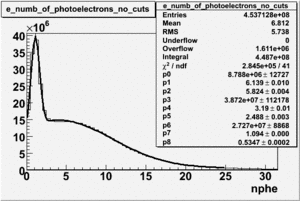
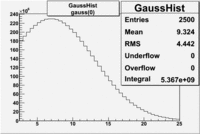
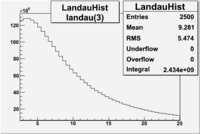
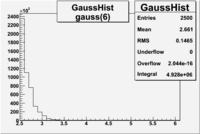
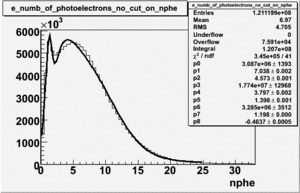
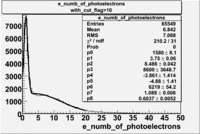
An estimate of the pion contamination in the electron candidates from the 5 GeV data set appears below. Cuts are applied on the electron candidates based on the ratio of the energy deposited by the electron candidate in the electron calorimeter to the particles momentum measured by track reconstruction using hits in the drift chamber . As reported at the last teleconference on 1/20/09, these cuts were taken from Media:Yelena_Prok_Measurement_of_The_Spin_structure_Function_of_The_Proton_in_The_Resonance_Region_Thesis.pdf and applied to the 5 GeV data sample. The number of photoelectrons measured by the cherenkov detector is shown below. The goal is to estimate the number of pions which contaminate the electron candidate sample. This is done by fitting the photoelectron distribution to 2 gaussian distributions and a Landau distribution. Integrals of the fits over the region of interest are used to determine the pion contamination to the electron candidates.
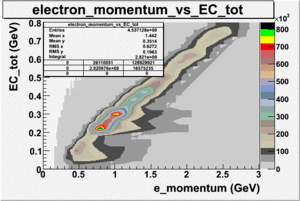
Number of photoelectrons and EC_tot/P vs nphe for Pions and Electrons when e_momentum < 3 GeV
| Momentum (GeV) | /P | /P | Cherenkov cut |
| e_momentum<3 | >0.2 | >0.08 | nphe>2.5 |
| Distributions | amplitude | mean | width | amplitude | mean | width |
|---|---|---|---|---|---|---|
| without cuts | with cuts(, , e_momentum<3 GeV) | |||||
| gauss(0) | p0=8.788e+06 +\-12727 | p1=6.139 +\-0.010 | p2=5.824 +\-0.004 | p0=4.604e+06 +\-6281 | p1=6.956 +\-0.010 | p2=6.056 +\-0.005 |
| landau(3) | p3=3.872e+07 +\-112178 | p4=3.19 +\-0.01 | p5=2.488 +\-0.003 | p3=1.426e+07 +\-56395 | p4=4.032 +\-0.008 | p5=2.497 +\-0.004 |
| gauss(6) | p6=2.727e+07 +\-8868 | p7=1.094 +\-0.000 | p8= 0.5347 +\-0.0002 | p6=9.694e+06 +\-4903 | p7=1.116 +\-0.000 | p8= 0.5185 +\-0.0004 |
- 1.) Electrons in the sample
Electrons in the sample(using all cuts except nphe>2.5) =
- 2.) Electrons in the sample using all cuts including nphe>2.5 cut
Electrons in the sample(including nphe>2.5 cut) =
- Conclusion
- Using only EC cuts, electrons in the sample are 60 %, after using the cut on the number of photoelectrons the pion contamination decreased and 69 % of the particles are electrons, that means pion contamination is 31 %. It decreased by 9 %.
If we assume that the photoelectrons from electrons are described by the Gaussian and landau distribution and that the pions are only in the gaussian distribution then we would expect our electron candidates to have a pion contamination of .
- For Pions
In this case, Josh's pion cut code was used. The number of entries decreased by ~ 20 %.
- For Electrons
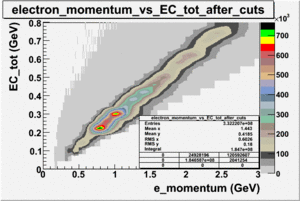
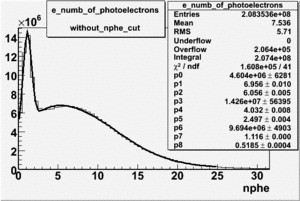
In order to remove the peak around ~ 1.5 PE and some high energy pions which have enough energy to cause the Cherenkov radiation the cut on nphe was applied. The number of entries after applying the following cuts - , e_momentum < 3 GeV and nphe > 2.5 decreased by 65.31 %.
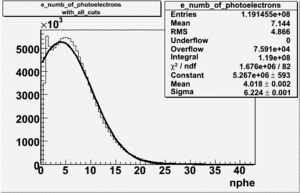
Number of photoelectrons and EC_tot/P vs nphe for Pions and Electrons when e_momentum > 3 GeV
| Momentum (GeV) | /P | /P | Cherenkov cut |
| e_momentum<3 | >0.24 | >0.06 | nphe>0.5 |
| Distributions | amplitude | mean | width | amplitude | mean | width |
|---|---|---|---|---|---|---|
| without cuts | with cuts(, , e_momentum>3 GeV) | |||||
| gauss(0) | p0=8.788e+06 +\-12717 | p1=6.139 +\-0.01 | p2=5.824 +\-0.004 | p0=3.087e+06 +\-1393 | p1=7.038 +\-0.002 | p2=4.573 +\-0.001 |
| landau(3) | p3=3.872e+07 +\- 112058 | p4=3.19 +\-0.01 | p5=2.488 +\-0.003 | p3=1.774e+07 +\-12968 | p4=3.797 +\-0.002 | p5=1.398 +\-0.001 |
| gauss(6) | p6=2.727e+07 +\- 8869 | p7=1.094 +\- 0.000 | p8= 0.5347 +\- 0.0002 | p6=3.285e+06 +\-3512 | p7=1.198 +\-0.000 | p8= -0.4637 +\-0.0005 |
- 1.) Electrons in the sample
Electrons in the sample(using all cuts except nphe>0.5) =
- 2.) Electrons in the sample using all cuts including nphe>0.5 cut
Electrons in the sample(all cuts) =
- Conclusion
- The pion contamination is this case is the same as it was before using the cut nphe>0.5 cut. The pion contamination is 45 % in the sample.
If we assume that the photoelectrons from electrons are described by the Gaussian and landau distribution and that the pions are only in the gaussian distribution then we would expect our electron candidates to have a pion contamination of .
- For Pions
In this case, Josh's pion cut code was used. The number of entries decreased by ~ 20 % .
- For Electrons
In order to remove the peak around ~ 1.5 PE and some high energy pions which have enough energy to cause the Cherenkov radiation the cut on nphe was applied. The number of entries after applying the following cuts - , e_momentum > 3 GeV and nphe > 0.5 decreased by 73 %.
Repeat the above calculation using Nevzat's cuts.
http://www.jlab.org/Hall-B/secure/eg1/EG2000/nevzat/GEOM_CC_CUTS/
1/29/09
We are interested in measuring the semi-inclusive pion asymmetry for both proton and deuteron targets using the 5-6 GeV EG1b data set. Our goal will be to investigate fragmentation and establish a procedure for extracting within the CLAS 12 GeV program. We begin the analysis using the EG1 DSTs created from "cooked" data files. Our first goal is evaluate the cuts used by others to improved the identification of scattered electrons in the data sample.
Cherenkov signal
Cherenkov PE Calculation
As shown in the wiki section, Particle_Identification#Cherenkov,
the expected number of photoelectrons produced by electrons traversing the CLAS cherenkov detector would be
if you assume a of 1 for the detected electrons in our data sample.
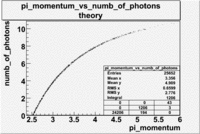
The expected number of photoelectrons in the CLAS cherenkov detector for reconstructed pion energies in the EG1 data set is shown in the graph below.
Our theoretical expectation, based on the description of the CLAS cherenkov detector suggests, that pions can generate up to about 10 photoelectrons compared with the 13 photoelectrons that can be generated by electrons. While the cherenkov detector can distinguish a 4 photoelectron signal generated by pions of momentum 3 GeV or less from the 10 photoelectrons generated by the typical detected electron, high momentum pions would generate photoelectron signals which are comparable to the photoelectrons generated by an electron.
Measured CLAS Cherenkov signal
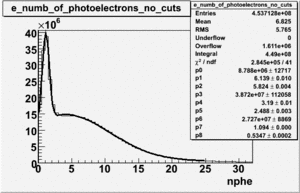
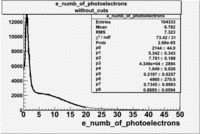
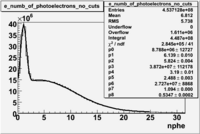
Electrons
The cherenkov signal measured in CLAS for particles identified as electrons by the tracking algorithm is shown below. There are two distributions present. One distribution is centered around 0.7 PEs and the second distribution is at 5.3 PEs when two gaussians and a Landau distribution are combined and fit to the spectrum.
- PE Fit equation (Osipenko's CLAS Note 2004-20 File:CLAS Note-2004-020.pdf)
The CLAS note above says 2 Poisson convolution by a gaussian are used to fit NPE histogram. The Poisson distribution starts to look like a gaussian when the Poisson mean value is larger than 4. Our electron candidates theoretically have NPE = 13 and pions have NPE>4 when the pion energies are above 3 GeV. We seem to get good fits if we use 2 Gaussians convoluted with a Landau.
As we will show below, the first peak is due to the misidentification of a negative pion as an electron.
Reconstruction of an electrons trajectory through the CLAS drift chambers can be done using either 5 or 6 super layers. Do tracks reconstructed using 5 superlayers generate cherenkov signals which differ from tracks reconstructed using all 6 DC superlayers? The track reconstruction algorithm records the number of superlayers used for the track reconstructions. This number is recorder in the EG1 DST files within the "flag" variable. If the "flag" variable in the DST is larger than 10, then 6 superlayers were used for the track reconstruction. The cherenkov spectrum below is observed for particles identified as electrons in the EG1 data in which 6 superlayers have been used to determine their trajectory.
The table below compares the cherekov spectrum fit values for particles identified as electrons with and without the 6 superlayer requirement. If 6 superlayers are required for the electron reconstruction, the high PE gaussian distribution mean changes from 5.3 PEs to 3.8 PEs and is not not consistent within 2 standard deviations of the fit errors. The LOW PE gaussian distribution, the suspected pion contamination, mean changes from 0.7 to 1.0 PEs.
The cuts decreases the number of entries by 37.17 %. It is believed that the Gaussian distribution centered around 1 PE is due to high energy pions(>2.5GeV). Neither of these distributions is consistent with the theoretical predictions made above suggesting that there are some light collection inefficiencies within the cherenkov detector.
Table: Cherenkov fit values
| Distributions | amplitude | mean | width | amplitude | mean | width |
|---|---|---|---|---|---|---|
| without cuts | with cut(flag>10) | |||||
| gauss(0) | p0=2144+/-44.0 | p1=5.342+/-0.343 | p2=7.761+/-0.188 | p0=1580+/-8.1 | p1=3.75+/-0.06 | p2=8.486+/-0.042 |
| landau(3) | p3=4.349e+04+/-2894 | p4=1.049+/-0.026 | p5=0.2197+/-0.0257 | p3=8600+/-3648.7 | p4=-3.861+/-1.414 | p5=-4.88+/-1.41 |
| gauss(6) | p6=4960+/-270.6 | p7=0.7345+/-0.0983 | p8=0.8885+/-0.0594 | p6=6219+/-54.2 | p7=1.088+/-0.006 | p8=0.6037+/-0.0052 |
The plots below show the event population intensity as a function of the electron candidates momentum measured by tracking and the number of photoelectrons observed in the cherenkov detector
| Experiment | B>0 | without cuts | flag>10 | 5<nphe<15 | 5<nphe<15 and flag>10 |
|---|---|---|---|---|---|
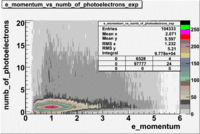
|
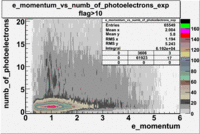
|
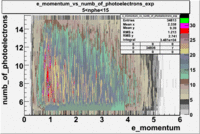
|
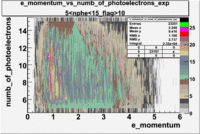
|
Pions()
- _Momentum_vs_Number_of_Photons
The histograms presented below show the event population intensity for the pion momentum and the number of photoelectrons generated by the pions. One can see that after applying cuts on NPhE and flag the mean value is around 1.
| Experiment | B>0 | without cuts | e_flag>10 | 0<e_nphe<5 | 0<nphe<5 and e_flag>10 |
|---|---|---|---|---|---|
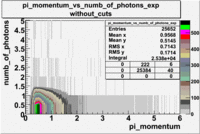
|
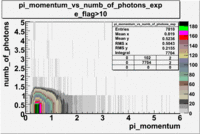
|
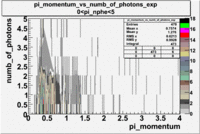
|
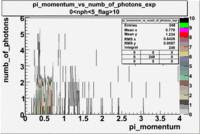
|
Electron-pion contamination
Osipenko's CLAS Note 2004-20 File:CLAS Note-2004-020.pdf
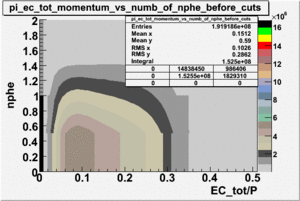
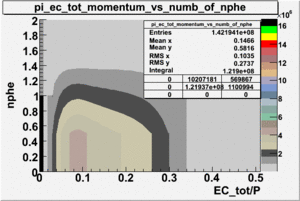
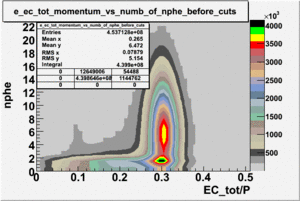
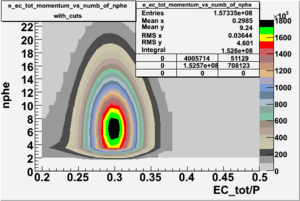
- EC_tot/P_vs_Number_of_Photoelectrons and EC_inner/P_vs_Number_of_Photoelectrons
Two types of cuts were applied on the distributions below, one on the energy deposited to the inner calorimeter and another one on the total energy absorbed by the calorimeter , to improve the electron particle identification. In this case we used the DST file dst27095_05, the beam energy is 5.735 GeV and target NH3.
| without cut | _vs_nphe() | _vs_nphe () | _vs_nphe() |
|---|---|---|---|
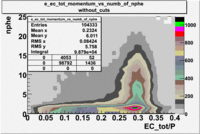
|
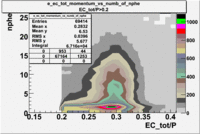
|
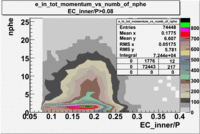
|
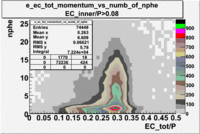
|
| _vs_nphe() | _vs_nphe( and ) | _vs_nphe ( and ) |
|---|---|---|

|
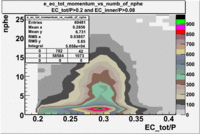
|
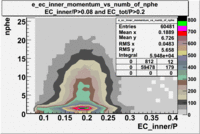
|
21-07-2010
Cuts
The correct identification of an electron and a pion is the main requirement for a semi-inclusive analysis. unfortunately, the pion is able to generate cerenkov radiation an as a result be misidentified as an electron. This contamination of the electron sample is removed using the cuts on the energy deposited in the electromagnetic calorimeter, the number of photoelectrons in the Cherenkov counter and fiducial cuts on the detector acceptance.
The energy deposition in the calorimeter for electrons and pions is different. Pions are minimum ionizing charge particles depositing into the calorimeter which is independent of the pion's momentum once the momentum is above ~ 0.08 GeV. On the other hand, electrons produce photoelectrons and create electromagnetic shower releasing the energy into the calorimeter which is proportional to their momentum. In order to remove contamination due to the energy deposition in the calorimeter the following cut was introduced: . The cut was also applied to the energy collected in the inner part of the calorimeter: , because the ratio of the energy deposited in the total to the inner calorimeter depends on the thickness of the detector and is a constant.
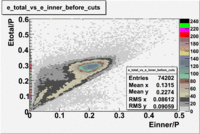
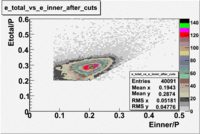
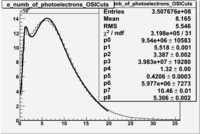
In addition to the cut on the energy deposited into the electromagnetic calorimeter, the misidentified electrons were excluded requiring a signal in the threshold CLAS Cherenkov detector. Pion's misidentified as electrons have been shown to produce around ~1.5 photoelectons in the cherenkov detector, as shown below. Geometrical cuts on the location of the particle at the entrance to the cerenkov detector were applied to reduce the pion contamination. The second histogram below shows that after cuts the peak around 1.5 is substantially reduced.
| No cuts | OSI Cuts |
phi_angle_in_CM_Frame_vs_Relative_Rate
Because of wide range of kinematics, was measured only for certain lepton scattering angles and invariant mass (W). Applying above described cuts: EC_inner>0.06, EC_tot/p>0.2, nphe>2.5 and , for the following invariant mass and the vs relative rate distribution is shown below on the graph and compared with E99-107 data, which by itself is in agreement with the models.
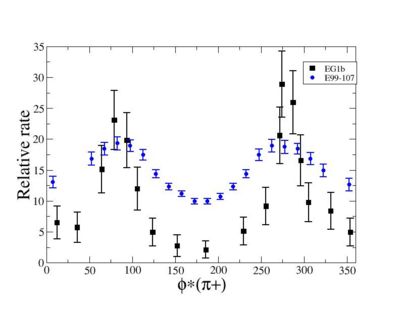 vs Relative rate for fixed and <ref name="Park2008" > Bogus text</ref> <ref> http://clasweb.jlab.org/cgi-bin/clasdb/msm.cgi?eid=14&mid=16&data=on </ref> |
The EG1b data for kinematics chosen above show the same shape as E99-107 data.
If you follow the link below, you can find the comparison for the wide range of kinematics:
Phi_angle_in_CM_frame_for_different_runs
Electron Efficiency Ratio
Used NH3 target runs with positive and negative torus. EC , nphe and OSI cuts are applied. Only electron was required.
| File number | electron | electron |
| B<0 |  |
|
| B>0 |  |
|
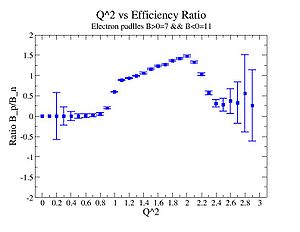
Below is the graph of electron efficiency ratio when electron_paddle_number=7 for positive torus(Bp) and electron_paddle_number=11 for negative torus(B_n)
Media:electronefficiencyratioBp7Bn11.txt
In this case we required positive pion and electron and applied cut on ()
| X_bj | B_n/B_p Rates |
|---|---|
| 0.14 | 0.25 0.55 |
| 0.15 | 0.74 0.27 |
| 0.17 | 1.07 0.18 |
| 0.19 | 1.3 0.13 |
| 0.2 | 1.4 0.14 |