Particle Identification

From New IAC Wiki
Jump to navigation Jump to search

EG1 run database
run summary
polarization info


Particle Identification

Cherenkov

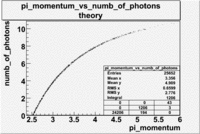
Cherenkov Theory

When the velocity of a charged particle is greater than the local phase velocity of light or when it enters a medium with different optical properties the charged particle will emit photons. The Cherenkov light is emitted under a constant angle [math]\theta_c[/math] - the angle of Cherenkov radiation relative to the particle's direction. It can be shown geometrically that the cosine of the Cherenkov radiation angle is anti-proportional to the velocity of the charged particle

[math]cos \theta_c=\frac{1}{n \beta}[/math]

where [math]\beta c[/math] is the particle's velocity and n - index of refraction of the medium.The charged particle in time t travels [math]\beta c t[/math] distance, while the electromagnetic waves - [math]\frac{c}{n}t[/math]. For a medium with given index of refraction n there is a threshold velocity [math]\beta_{thr}=\frac{1}{n}[/math], below [math]\beta_{thr}[/math] no radiation can take place. This process may be used to observe the passage of charged particles in a detector which can measure the produced photons.

The number of photons produced per unit path length of a particle with charge ze and per unit energy interval of the photons is proportional to the sine of the Cherenkov angle[1]

[math]\frac{d^2 N}{dEdx}=\frac{\alpha z^2}{\hbar c}sin ^2 \theta_c=\frac{\alpha z^2}{\hbar c}[1-\frac{1}{\beta^2 n^2 (E)}][/math]


[math]\frac{d^2 N}{d\lambda dx} = \frac{2 \pi \alpha z^2}{\lambda^2}[1-\frac{1}{\beta^2 n^2 (\lambda)}][/math]

[math]\beta=\frac{v}{c}=\frac{pc}{\sqrt{(pc)^2 + (mc^2)^2}}[/math]

after deriving the Taylor expansion of our function and considering only the first two terms, we get
[math]\frac{d^2 N}{dEdx}=\frac{\alpha z^2}{\hbar c}[\beta^2 n^2 (E) - 1][/math]


\frac{\alpha z^2}{\hbar c}sin ^2 \theta_c= The gas used in the CLAS Cerenkov counter is perfluorobutane [math]C_4 F_{10}[/math] with index of refraction equal to 1.00153.


Electrons

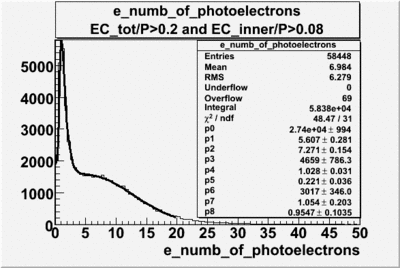
The calculation of the number of photoelectrons emitted by electrons is shown below. Electron mass [math]m_e = 0.000511GeV[/math], [math]n=1.00153[/math] and [math]\beta=\frac{p}{E} = 1[/math], because mass of the electron is negligible and also [math]\frac{\alpha}{\hbar c}=370[ eV^{-1} cm^{-1}] [/math]

The Hall B cherenkov detector is [math]\sim \; 0.7[/math] m thick radiator. We assume the PMTs used to collect light have a constant quantum efficiency of 8% for photons with wavelength between 300 and 600 nm.

[math]\frac{dN}{dx} [/math] [math]= 2 \pi \alpha z^2 [{\beta^2 n^2 (\lambda)} - 1]\int_{300nm}^{600nm} \frac{1}{\lambda^2} d\lambda \times (0.08)=[/math]
[math]= 2 \pi \alpha z^2 [{\beta^2 n^2 (\lambda)} - 1] (\frac {1}{\lambda})|_{600nm}^{300nm} \times (0.08) [/math]=
[math]= 2\times 3.14 \times \frac{1}{137} \times 1^2 \times [1.00153^2 - 1] \times \frac{1}{600} \times 0.08 [nm^{-1}] = [/math]
[math]= 19 \times 10^{-9} [nm^{-1}][/math]

For the number of photoelectrons we have the following

[math] N = 19 \times 10^{-9} \times 0.7 m [\frac{10^9}{m}] = 13.3 [/math]

That means the number of photoelectrons should be about 13.

Used file dst27095_05.B00 energy=5.7GeV and torus=2250(B>0). Target NH3

E momentum vs numb of photoelectrons 27095 theory.gif

Pions([math]\pi^-[/math])

The threshold energy for pions is ~2.5 GeV and for electrons 9 MeV.

Example for [math]\pi^-[/math]

[math]m_{\pi^-}=139.57[\frac{MeV}{c^2}][/math], momentum [math]p=mv=3 [\frac{GeV}{c}][/math] and n=1.00153

where [math]\frac{\alpha}{\hbar c}=370[ eV^{-1} cm^{-1}] [/math]

The Hall B cherenkov detector is [math]\sim \; 0.7[/math] m thick radiator. We assume the PMTs used to collect light have a constant quantum efficiency of 8% for photons with wavelength between 300 and 600 nm.

[math]\frac{dN}{dx} = \frac{2 \pi \alpha z^2}{\lambda^2}[1-\frac{1}{\beta^2 n^2 (\lambda)}]=[/math]
[math]= 2 \pi \alpha z^2 [1-\frac{1}{\beta^2 n^2 (\lambda)}]\int_{300nm}^{600nm} \frac{1}{\lambda^2} d\lambda \times (0.08)=[/math]
[math]= 2 \pi \alpha z^2 [1-\frac{1}{\beta^2 n^2 (\lambda)}] (\frac {1}{\lambda})|_{600nm}^{300nm} \times (0.08) [/math]=
[math]= 2\times 3.14 \times \frac{1}{137} \times 1^2 \times [1-\frac{1}{0.998919^2 \times 1.00153^2}] \times \frac{1}{600} \times 0.08 [nm^{-1}] = [/math]
[math]= 5.465 \times 10^{-9} [nm^{-1}][/math]

For the number of photons we have the following(for pions)

[math] N = 5.465 \times 10^{-9} \times 0.7 m [\frac{10^9}{m}] = 3.8255 [/math]

Used file dst27095_05.B00 energy=5.7GeV and torus=2250(B>0). Target NH3

Pi momentum vs numb of photons 27095 theory.gif

CLAS Cherenkov signal

Electrons

The cherenkov signal measured in CLAS for particles identified as electrons by the tracking algorithm is shown below. There are two distributions present. One distribution is centered around 1.5 PEs and the second distribution is at 8 PEs when two gaussians and a Landau distribution are combined and fit to the spectrum. As we will show below, the first peak is due to the misidentification of a negative pion as an electron.

PE Fit equation
[math]N_{pe}= p_0 e^{-0.5 \left (\frac{x-p_1}{p_2} \right )^2} + p4\frac{1}{1-\left(\frac{x-p5}{p6}\right )} + p_6 e^{-0.5 \left (\frac{x-p_7}{p_8} \right )^2}[/math]
File:Gaussian fitting function.pdf

C.Lanczos, SIAM Journal of Numerical Analysis B1 (1964), 86.
File:C.Lanczos SIAM Journal of Numerical Analysis B1 1964 86.pdf


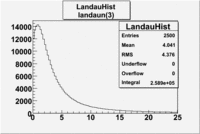
normalized fitting functions Landau and Landaun difference for me 

//__[2] [3] ____________________________________________________________________________
Double_t TMath::Landau(Double_t x, Double_t mpv, Double_t sigma, Bool_t norm)
{
  // The LANDAU function with mpv(most probable value) and sigma.
  // This function has been adapted from the CERNLIB routine G110 denlan.
  // If norm=kTRUE (default is kFALSE) the result is divided by sigma
  static Double_t p1[5] = {0.4259894875,-0.1249762550, 0.03984243700, -0.006298287635,   0.001511162253};
  static Double_t q1[5] = {1.0         ,-0.3388260629, 0.09594393323, -0.01608042283,    0.003778942063};
  static Double_t p2[5] = {0.1788541609, 0.1173957403, 0.01488850518, -0.001394989411,   0.0001283617211};
  static Double_t q2[5] = {1.0         , 0.7428795082, 0.3153932961,   0.06694219548,    0.008790609714};
  static Double_t p3[5] = {0.1788544503, 0.09359161662,0.006325387654, 0.00006611667319,-0.000002031049101};
  static Double_t q3[5] = {1.0         , 0.6097809921, 0.2560616665,   0.04746722384,    0.006957301675};
  static Double_t p4[5] = {0.9874054407, 118.6723273,  849.2794360,   -743.7792444,      427.0262186};
  static Double_t q4[5] = {1.0         , 106.8615961,  337.6496214,    2016.712389,      1597.063511};
  static Double_t p5[5] = {1.003675074,  167.5702434,  4789.711289,    21217.86767,     -22324.94910};
  static Double_t q5[5] = {1.0         , 156.9424537,  3745.310488,    9834.698876,      66924.28357};
  static Double_t p6[5] = {1.000827619,  664.9143136,  62972.92665,    475554.6998,     -5743609.109};
  static Double_t q6[5] = {1.0         , 651.4101098,  56974.73333,    165917.4725,     -2815759.939};
  static Double_t a1[3] = {0.04166666667,-0.01996527778, 0.02709538966};
  static Double_t a2[2] = {-1.845568670,-4.284640743};
  if (sigma <= 0) return 0;
  Double_t v = (x-mpv)/sigma;
  Double_t u, ue, us, den;
  if (v < -5.5) {
     u   = TMath::Exp(v+1.0);
     if (u < 1e-10) return 0.0;
     ue  = TMath::Exp(-1/u);
     us  = TMath::Sqrt(u);
     den = 0.3989422803*(ue/us)*(1+(a1[0]+(a1[1]+a1[2]*u)*u)*u);
  } else if(v < -1) {
     u   = TMath::Exp(-v-1);
     den = TMath::Exp(-u)*TMath::Sqrt(u)*
            (p1[0]+(p1[1]+(p1[2]+(p1[3]+p1[4]*v)*v)*v)*v)/
            (q1[0]+(q1[1]+(q1[2]+(q1[3]+q1[4]*v)*v)*v)*v);
  } else if(v < 1) {
     den = (p2[0]+(p2[1]+(p2[2]+(p2[3]+p2[4]*v)*v)*v)*v)/
           (q2[0]+(q2[1]+(q2[2]+(q2[3]+q2[4]*v)*v)*v)*v);
  } else if(v < 5) {
     den = (p3[0]+(p3[1]+(p3[2]+(p3[3]+p3[4]*v)*v)*v)*v)/
           (q3[0]+(q3[1]+(q3[2]+(q3[3]+q3[4]*v)*v)*v)*v);
  } else if(v < 12) {
     u   = 1/v;
     den = u*u*(p4[0]+(p4[1]+(p4[2]+(p4[3]+p4[4]*u)*u)*u)*u)/
               (q4[0]+(q4[1]+(q4[2]+(q4[3]+q4[4]*u)*u)*u)*u);
  } else if(v < 50) {
     u   = 1/v;
     den = u*u*(p5[0]+(p5[1]+(p5[2]+(p5[3]+p5[4]*u)*u)*u)*u)/
               (q5[0]+(q5[1]+(q5[2]+(q5[3]+q5[4]*u)*u)*u)*u);
  } else if(v < 300) {
     u   = 1/v;
     den = u*u*(p6[0]+(p6[1]+(p6[2]+(p6[3]+p6[4]*u)*u)*u)*u)/
               (q6[0]+(q6[1]+(q6[2]+(q6[3]+q6[4]*u)*u)*u)*u);
  } else {
     u   = 1/(v-v*TMath::Log(v)/(v+1));
     den = u*u*(1+(a2[0]+a2[1]*u)*u);
  }
  if (!norm) return den;
  return den/sigma;
}

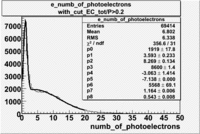
Fitting the Histograms

root [13] e_numb_of_photoelectrons->Draw();   

root [2] g3= new TF1("g3","gaus(0)+landau(3)+gaus(6)",0,20);

To get fit parameters for g3 we should fit individually each of them(gaus(0),landau(3),gaus(6))

root [3] g3->SetParameters(2.3e3,8,8.1,8.6e+3,8.6e-1,1.6,8.6e+3,8.6e-1,1.6,8.6e3)

root [11] e_numb_of_photoelectrons->Fit("g3","R+");
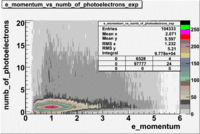
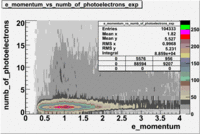
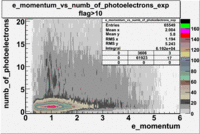
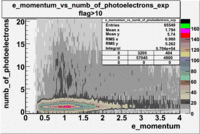
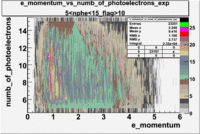
e_Momentum_vs_Number_of_Photoelectrons

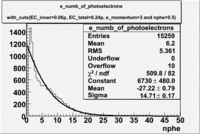
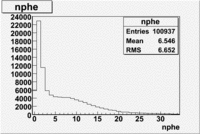
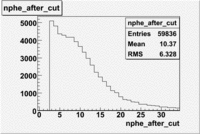
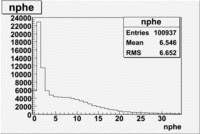
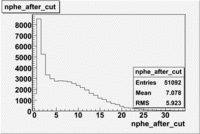
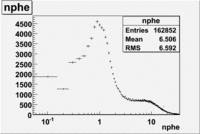
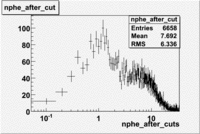
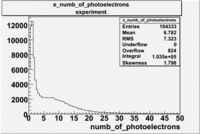
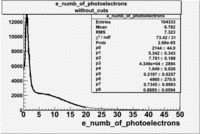
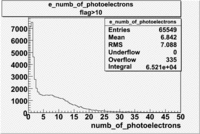
The flag cut applied on the number of photoelectrons means that in CLAS detector instead of 5 superlayers were used 6 of them in track fit. As one can see from the histograms of the Number of photoelectrons, the cut on flag does not have effect on the peak around 1.5phe and decreases the number of entries by 37.17 %. The peak is due to a high energy pions(>2.5GeV), which have enough momentum to emit Cherenkov light and also because of the bad collection of light, there are a particular polar and azimuthal combination of angles where The Cherencov Detector cannot receive emitted light. .

Number of photoelectrons


Data
E number of photoelectrons 27095 1.gif E number of photoelectrons 27095 fits.gif
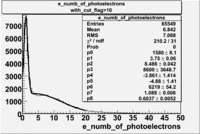
E number of photoelectrons 27095 flag 10 1.gif E number of photoelectrons 27095 flag 10 fit with cut.gif


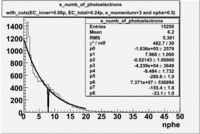
Table: Cherenkov fit values

Distributions amplitude mean width amplitude mean width
without cuts with cut(flag>10)
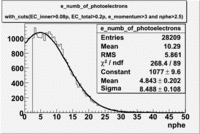
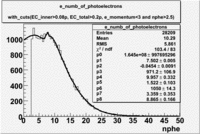
gauss(0) p0=2144+/-44.0 p1=5.342+/-0.343 p2=7.761+/-0.188 p0=1580+/-8.1 p1=3.75+/-0.06 p2=8.486+/-0.042
landau(3) p3=4.349e+04+/-2894 p4=1.049+/-0.026 p5=0.2197+/-0.0257 p3=8600+/-3648.7 p4=-3.861+/-1.414 p5=-4.88+/-1.41
gauss(6) p6=4960+/-270.6 p7=0.7345+/-0.0983 p8=0.8885+/-0.0594 p6=6219+/-54.2 p7=1.088+/-0.006 p8=0.6037+/-0.0052



When flag cut(flag>10 cut means that 6 superlayers were used in track fit) was applied the number of entries decreased by 37.17 % and the mean value for the number of photoelectrons is about 7-8. After 5<nphe<15 cut, the number of entries decreased by 66.63 %.The mean value of the nphe is ~9 which agrees with theory(mean value ~13).


Experiment B>0 without cuts flag>10 5<nphe<15 5<nphe<15 and flag>10
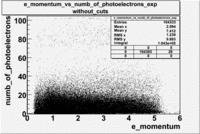
E momentum vs numb of photoelectrons 27095 exp without cuts 1.gif

E momentum vs numb of photoelectrons 27095 exp without cuts 2.gif E momentum vs numb of photoelectrons 27095 exp without cuts 3.gif

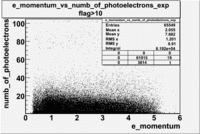
E momentum vs numb of photoelectrons 27095 exp with cuts flag 10 1.gif

E momentum vs numb of photoelectrons 27095 exp with cuts flag 10 2.gif E momentum vs numb of photoelectrons 27095 exp with cuts flag 10 3.gif

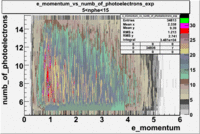
E momentum vs numb of photoelectrons 27095 exp with cuts ? nphe ?.gif E momentum vs numb of photoelectrons 27095 exp with cuts 5 nphe 15 flag 10.gif

Pions([math]\pi^-[/math])

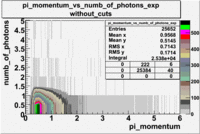
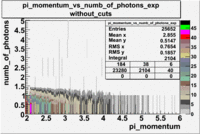
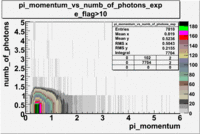
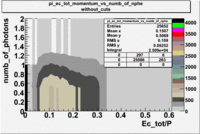
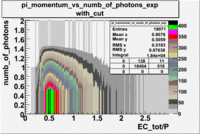
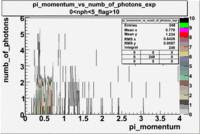
[math]\pi^-[/math]_Momentum_vs_Number_of_Photons

After e_flag>10 cut, the number of entries decreased by 30.45 % and the mean value for the number of photons is ~9


Experiment B>0 without cuts e_flag>10 0<e_nphe<5 0<nphe<5 and e_flag>10
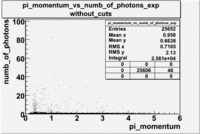
Pi momentum vs numb of photoelectrons 27095 exp without cuts 1 1.gif

Pi momentum vs numb of photoelectrons 27095 exp without cuts 2 1.gif Pi momentum vs numb of photoelectrons 27095 exp without cuts 3 1.gif

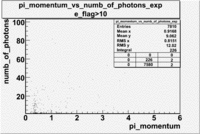
Pi momentum vs numb of photoelectrons 27095 exp with cuts flag 10 1 1.gif

Pi momentum vs numb of photoelectrons 27095 exp with cuts flag 10 2 1.gif Pi momentum vs numb of photoelectrons 27095 exp with cuts flag 10 3 1.gif

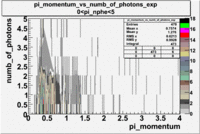
Pi momentum vs numb of photoelectrons 27095 exp with cuts ? nphe ?.gif Pi momentum vs numb of photoelectrons 27095 exp with cuts 0 nphe 5 flag 10.gif

Calorimeter

Electron-pion contamination

Osipenko's CLAS Note 2004-20 File:CLAS Note-2004-020.pdf

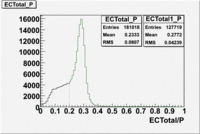
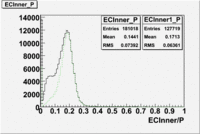
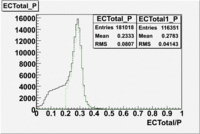
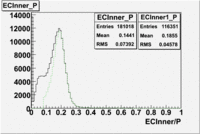
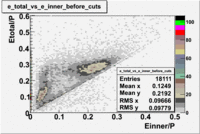
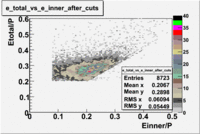
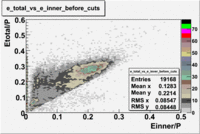
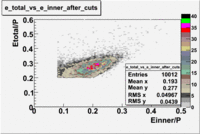
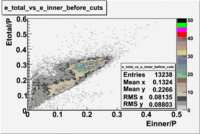
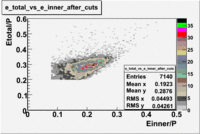
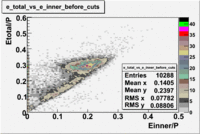
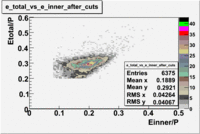
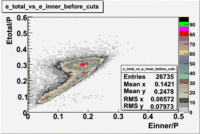
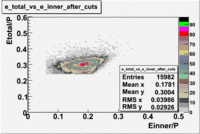
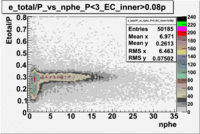
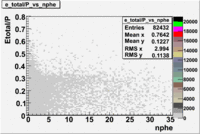
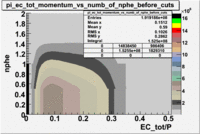
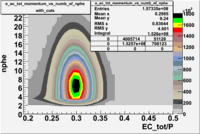
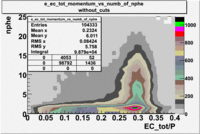
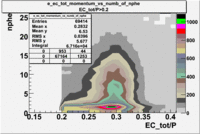
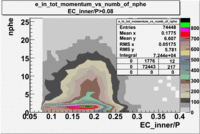
EC_tot/P_vs_Number_of_Photoelectrons and EC_inner/P_vs_Number_of_Photoelectrons

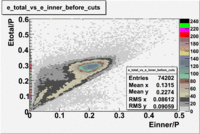
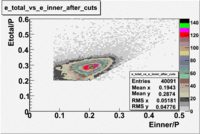
Two types of cuts were applied on the distributions below, one on the energy deposited to the inner calorimeter [math]EC_{inner}/P\gt 0.08[/math] and another one on the total energy absorbed by the calorimeter [math]EC_{tot}/P\gt 0.2[/math], to improve the electron particle identification. In this case was used dst27095_05 file, the beam energy is 5.735 GeV and target NH3.

without cut [math]EC_{tot}/P[/math]_vs_nphe([math]EC_{tot}/P\gt 0.2[/math]) [math]EC_{inner}/P[/math]_vs_nphe ([math]EC_{inner}/P\gt 0.08[/math]) [math]EC_{tot}/P[/math]_vs_nphe([math]EC_{inner}/P\gt 0.08[/math])
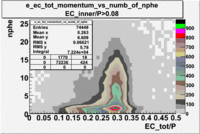
Ec tot momentum vs numb of phe 27095 without cut.gif Ec tot momentum vs numb of phe 27095 with cut.gif Ec inner momentum vs numb of phe 27095 with cut ec inner momentum 0.08.gif Ec tot momentum vs numb of phe 27095 with cut ec inner momentum 0.08.gif


[math]EC_{inner}/P[/math]_vs_nphe([math]EC_{tot}/P\gt 0.2[/math]) [math]EC_{tot}/P[/math]_vs_nphe([math]EC_{tot}/P\gt 0.2[/math] and [math]EC_{inner}/P\gt 0.08[/math]) [math]EC_{inner}/P[/math]_vs_nphe ([math]EC_{tot}/P\gt 0.2[/math] and [math]EC_{inner}/P\gt 0.08[/math])
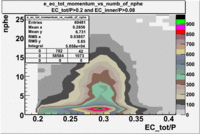
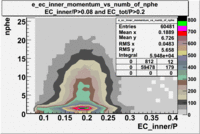
Ec inner momentum vs numb of phe 27095 with cut ec tot momentum 0.2.gif Ec tot momentum vs numb of phe 27095 with cut ec inner momentum 0.08 and ec tot momentum 0.2.gif Ec inner momentum vs numb of phe 27095 with cut ec tot momentum 0.2 and ec inner momentum0.08.gif



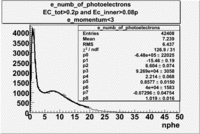
From the EC_tot/P_vs_Number_of_Photoelectrons histogram one can see that the released energy fraction([math]EC_{tot}/P[/math]) at ~1.5 nphe peak is much smaller than it should be for electrons. In conclusion, the ~1.5 nphe peak is produced by the tail of negatively charged particles(pions). To eliminate negatively charged pions [math]EC_{tot}/P\gt 0.2[/math] cut is applied on Calorimeter. After the cut was applied the number of entries decreased by ~33.47%.

E numb of photoelectrons with cuts 27095 ec inner p 0.08 and ec tot p 0.2 file dst27095 fitted with normalized gaussian and landau.gif

Gausn 0 fitting Histogram.gifGausn 6 fitting Histogram.gifLandaun 3 fitting Histogram.gif

Pion contamination in the electron sample (without cuts) =
[math] = \frac {Integral(gauss(0))}{Integral(gauss(0) + landau(3) + gauss(6))} =[/math]
[math] = \frac{2.126 \times 10^6}{ 2.126 \times 10^6 + 2.589 \times 10^5 + 4.659 \times 10^5} = [/math]
[math] = 0.74575 [/math]

with cut([math]EC_{tot}/P\gt 0.2[/math]) with cut([math]EC_{inner}/P\gt 0.08[/math]) with cuts([math]EC_{inner}/P\gt 0.08[/math] and [math]EC_{tot}/P\gt 0.2[/math])
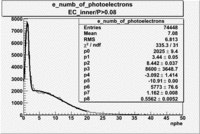
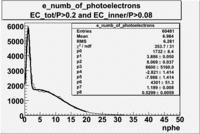
E numb of photoelectrons with cuts 27095 ec tot p 0.2.gif E numb of photoelectrons with cuts 27095 ec inner p 0.08.gif E numb of photoelectrons with cuts 27095 ec inner p 0.08 and ec tot p 0.2.gif
Distributions amplitude mean width amplitude mean width amplitude mean width
with cut([math]EC_{tot}/P\gt 0.2[/math]) with cut([math]EC_{inner}/P\gt 0.08[/math]) with cuts([math]EC_{inner}/P\gt 0.08[/math] and [math]EC_{tot}/P\gt 0.2[/math])
gauss(0) p0=1919+/-17.8 p1=3.593+/-0.233 p2=8.269+/-0.134 p0=2025+/-9.4 p1=3.44+/-0.05 p2=8.442+/-0.037 p0=1732+/-8.4 p1=3.886+/-0.050 p2=8.069+/-0.037
landau(3) p3=8600+/-1.4 p4=-3.063+/-1.414 p5=-7.138+/-0.000 p3=8600+/-3648.7 p4=-3.092+/-1.414 p5=-10.91+/-0.000 p3=8600+/-5160.0 p4=-2.821+/-1.414 p5=-7.986+/-1.414
gauss(6) p6=5568+/-69.1 p7=1.164+/-0.006 p8=0.543+/-0.008 p6=5773+/-76.6 p7=1.162+/-0.008 p8=0.5562+/-0.0052 p6=4301+/51.3 p7=1.189+/-0.008 p8=0.5299+/-0.0059


E numb of photoelectrons ec inner 0.08 ec total 0.2 e momentum 3GeV.gif

e_numb_of_photoelectrons with the following cuts [math]EC_{inner}/P\gt 0.08[/math], [math]EC_{tot}/P\gt 0.2[/math]. To eliminate the photons produced by the negatively charged pions was used the cut on the momentum e_momentum<3 GeV. Because the high energy pions are able to produce photons, which are misidentified with photoelectrons.


Electrons nphe with cuts ecinner 0.08p ectotal 0.2p emomentum 3 nphe 2.5 file dst27095 with gauss fit.gif Electrons nphe with cuts ecinner 0.08p ectotal 0.2p emomentum 3 nphe 2.5 file dst27095 with gauss landau fit.gif Electrons nphe with cuts ecinner 0.06p ectotal 0.24p emomentum 3 nphe 0.5 file dst27095 with gauss fit.gif Electrons nphe with cuts ecinner 0.06p ectotal 0.24p emomentum 3 nphe 0.5 file dst27095 with gauss landau fit.gif

Electron

Cuts

Calorimeter based cuts

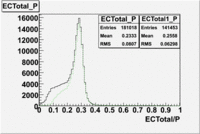
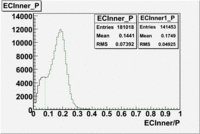
The distributions below represent two types of cuts applied to improve the electron particle identification (PID) using a 4 GeV electron beam incident on an NH3 target. The electron calorimeter is segmented into an inner[math]EC_{inner}[/math] and an outer[math]EC_{outer}[/math] region. The total energy absorbed by the calorimeter system is recorded in the variable [math]EC_{tot}[/math]. The momentum ([math]P[/math]) is calculated using the reconstructed track and the known torus magnetic field. The distributions of [math]EC_{tot}[/math] and [math]EC_{inner}[/math] are shown below where both have been divided by the electron momentum and no cuts have been applied.


[math]EC_{tot}\gt 0.2*p[/math]

Without any cuts we have 181018 entries. After using the following cut [math]EC_{tot}\gt 0.2*p[/math] we are getting 127719 entries, which is about 70.55% of 181018.

Etotal P using tot cut.gif Einner P using tot cut.gif

[math]EC_{inner}\gt 0.08*p[/math]

After the cut on the energy deposited into inner part of electron calorimeter, number of entries decreases by 22%.

Etotal P using inner cut.gif Einner P using inner cut.gif

Both cuts [math] EC_{tot}\gt 0.2*p [/math] and [math] EC_{inner}\gt 0.08*p [/math]

In case of using the cuts of the total deposited energy and the energy deposited into inner calorimeter number of entries decreases ~36%

Etotal P using both cuts.gif Einner P using both cuts.gif

summary table

The "# of triggers" columns represents the number of events which generated a signal above threshold in the calorimeter and the scintillator. The expected # of events column represents the number of reconstructed events with tracks that also make it through the cuts defined in the table.

The semi-inclusive analysis will focus on the 4 GeV and 6 GeV data which have both inbending and outbending torus settings. Specifically runs 28074 - 28579 ( 4 GeV) and Runs 27356 - 27499 and 26874 - 27198 (6 GeV)


Beam Energy Torus Current Begin Run End Run file used cuts # trig([math]10^6[/math]) expected # evts([math]10^6[/math]) p<3,[math]EC_{tot}\gt 0.2*p [/math],[math] EC_{inner}\gt 0.08*p[/math](%) p>3,[math]EC_{tot}\gt 0.24*p [/math],[math] EC_{inner}\gt 0.06*p[/math](%)
[math]EC_{tot}\gt 0.2*p[/math] [math]EC_{inner}\gt 0.08*p[/math] [math]EC_{tot}\gt 0.2*p [/math] and [math] EC_{inner}\gt 0.08*p[/math]
1606 1500 25488 25559 dst25504_02.B00 64% 49.5% 78% 60 3.2
1606 1946 25560 25605 44
1606 1500 25669 25732 dst25669_02.B00 64% 49% 78% 226 10
1606 1500 25742 26221 dst25754_02.B00 21% 11% 24% 3154 13.3
1606 -1500 26222 26359 dst26224_02.B00 4.6% 3% 6.6% 703 13.1
1724 -1500 27644 27798 dst27649_02.B00 4.8% 2.2% 5.9% 211 20
1724 1500 28512 28526 159
1724 -1500 28527 28532 93
2288 1500 27205 27351 dst27225_02.B00 20.2% 13% 25.6% 1647 16.1
2562 -1500 27799 27924 dst27809_02.B00 5.7% 4.6% 8.6% 1441 13.1
2562 -1500 27942 27995 dst27942_02.B00 6.1% 4.4% 8.9% 841 32.3
2562 1500 28001 28069 dst28002_02.B00 27.8% 13% 29.6% 1013 30.7
2792 -1500 27936 27941 dst27937_02.B00 6.7% 5% 9.9% 69 20.6
3210 -2250 28549 28570 436
4239 2250 28074 28277 dst28075_02.B00 35.3% 23.9% 40.5% 2278 19.6
4239 -2250 28280 28479 dst28281_02.B00 9.1% 9.4% 13.6% 2620 15.2
4239 2250 28482 28494 7
4239 -2250 28500 28505 107
4239 2250 28506 28510 dst28509_02.B00 29.5% 22% 36% 75 18.1
5627 2250 27356 27364 dst27358_02.B00 33.2% 27.8% 41.3% 56 19.4 44.6 40.1
5627 -2250 27366 27380 dst27368_02.B00 12.6% 14.8% 19.5% 130 13.6 25.3 8.8
5627 2250 27386 27499 dst27388_02.B00 33.4% 27.8% 41.4% 1210 20.2 44.8 40.1
5627 965 27502 27617 493
5735 -2250 26874 27068 dst26904_02.B00 13% 15% 20% 1709 19.9 25.6 9.1
5735 2250 27069 27198 dst27070_02.B00 33.3% 28.8% 42.2% 1509 15 46 40.2
5764 -2250 26468 26722 dst26489_02.B00 12.2% 14.4% 19.1% 1189 10 24.6 9.3
5764 0 26723 26775 268
5764 -2250 26776 26851 dst26779_02.B00 13.5% 15.5% 20.5% 662 15.9 26.4 9.2

Cut on the number of photoelectrons

In this case is used a cut on the number of photoelectrons, which is [math]nphe\gt 2.5[/math]. The plots below show the effect of the number of photoelectrons cuts on the Cerenkov distribution. We see that after using cut the number of entries decreases ~40.7%

Nphe before cut file 27070.gif Nphe1 after cut file 27070.gif


Used cuts [math]EC_{tot}\gt 0.24p[/math] and [math]EC_{inner}\gt 0.06p[/math]


Nphe before electron cuts file 27070.gif Nphe1 after electron cuts file 27070.gif


Used file dst28181_03(energy 4.2GeV). In this case was applied cuts on the polar angle([math]15\lt \theta\lt 20[/math]) and momentum([math]2.2\lt P\lt 2.6[/math]). Number of entries decreased by 96%(?????????????/)


Nphe before cuts file 28181.gif Nphe1 after cuts file 28181.gif

OSIPENKO cuts

Plot of [math]EC_{tot}/p[/math] vs [math]EC_{inner}/p[/math]

In this case is used file dst27070(Energy 5.735 GeV and Torus 2250) and are applied the following EC cuts: For ECtotal - [math]EC_{tot}\gt 0.2p[/math], for EC inner - [math]EC_{inner}\gt 0.08p[/math].

P<3

After using above cuts the number of entries decreases ~46%

E total vs e inner1 before cuts file dst27070.gif E total vs e inner1 after cuts file dst27070.gif

0.5<P<1

The number of entries decreased by ~51.8%

E total vs e inner1 before cuts P1 file dst27070.gif E total vs e inner1 after cuts P1 file dst27070.gif

1<P<1.5

The number of entries decreased approximately by 47.8%

E total vs e inner1 before cuts P1.5 file dst27070.gif E total vs e inner1 after cuts P1.5 file dst27070.gif

1.5<P<2

In this case the number of entries decreased by 46.1%

E total vs e inner1 before cuts P2 file dst27070.gif E total vs e inner1 after cuts P2 file dst27070.gif

2<P<2.5

In this case the number of entries decreased by 38%

E total vs e inner1 before cuts P2.5 file dst27070.gif E total vs e inner1 after cuts P2.5 file dst27070.gif

P>3

Used file dst27070(Energy 5.735 GeV and Torus 2250) and are applied the following EC cuts: For ECtotal - [math]EC_{tot}\gt 0.24p[/math], for EC inner - [math]EC_{inner}\gt 0.06p[/math].

The number of entries decreased by~40.2%

E total vs e inner1 before cuts P3 file dst27070.gif E total vs e inner1 after cuts P3 file dst27070.gif

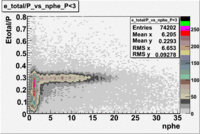
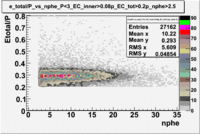
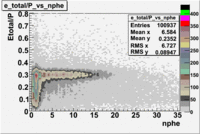
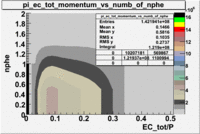
Plot of EC_tot/P vs nphe for Electrons

Used file dst27070(Energy 5.735 GeV and Torus 2250)

p<3 GeV

The graphs below represents all electron candidates having a momentum smaller than 3 GeV. Negatively charged pions are the most likely particle to be misidentified as an electrons by the tracking software. A negatively charged pion having a momentum of 3 GeV would generate less than ?? photons in the cerenkov counter. As a result the electron candidates which [math]n_{pe} \lt 1.xx [/math] are thought to be misidentified pions. The images which follow represent the effects of several cuts made for the purpose of removing misidentified particles.

E total vs nphe momentum cut file dst27070.gif


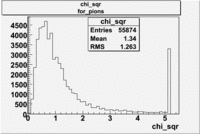
chi_sqr for pions

Chi sqr 27095 pions.gif

[math]\pi[/math]_Momentum_vs_Number_of_Photons for pions([math]\pi[/math])

Used file:27095_05.B00(energy=5.735GeV and torus=2250), everything is done for [math]\pi^-[/math]



p<3 GeV and [math]EC_{inner}\gt 0.08p[/math]

E total P vs nphe momentum Ec inner cuts file dst27070.gif

p<3 GeV, [math]EC_{inner}\gt 0.08p[/math] and [math]EC_{tot}\gt 0.2p[/math]

E total P vs nphe momentum EC inner EC total cuts file dst27070.gif

p<3 GeV, [math]EC_{inner}\gt 0.08p[/math], [math]EC_{tot}\gt 0.2p[/math] and nphe>2.5

E total P vs nphe momentum EC inner EC total nphe cuts file dst27070.gif

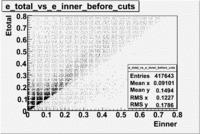
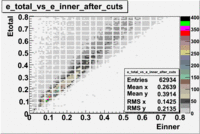
Plot of EC_total vs EC_inner

In this case file dst28181_03.B00 was used(Energy 4.2 GeV and Torus +2250). The following cuts were applied:[math]EC_{inner}\gt 0.005[/math], [math]EC_{tot}\gt 0.2*p[/math], ec_chi_sqr<0.1 and nphe>3.

Etotal vs Einner file dst28181 03 before cuts.gif Etotal vs Einner file dst28181 03 after cuts.gif

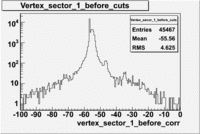
Raster and vertex correction

A raster calibration and a cut on the vertex distribution was made in order to select electrons from the polarized target, also the ones scattered from other materials in the beam path. A plot of the uncorrected vertex distribution is presented below for dst27070_02.B00 file(energy=5.7GeV Torus=2250)

Vertex before corrections dst27070 file.gif

Pion

Summary Table

Josh's Pion cuts code

Beam Energy Torus Current Begin Run End Run file used # trig([math]10^6[/math]) expected # evts([math]10^6[/math]) p>3,[math]EC_{tot}\lt 0.2*p [/math],[math] EC_{inner}\lt 0.08*p[/math](%) p<3,[math]EC_{tot}\lt 0.24*p [/math],[math] EC_{inner}\lt 0.06*p[/math](%)
1606 1500 25488 25559 dst25504_02.B00 60 3.2
1606 1500 25669 25732 dst25669_02.B00 226 10
1606 1500 25742 26221 dst25754_02.B00 3154 13.3
1606 -1500 26222 26359 dst26224_02.B00 703 13.1
1724 -1500 27644 27798 dst27649_02.B00 211 20
2288 1500 27205 27351 dst27225_02.B00 1647 16.1
2562 -1500 27799 27924 dst27809_02.B00 1441 13.1
2562 -1500 27942 27995 dst27942_02.B00 841 32.3
2562 1500 28001 28069 dst28002_02.B00 1013 30.7
2792 -1500 27936 27941 dst27937_02.B00 69 20.6
4239 2250 28074 28277 dst28075_02.B00 2278 19.6
4239 -2250 28280 28479 dst28281_02.B00 2620 15.2
4239 2250 28506 28510 dst28509_02.B00 75 18.1
5627 2250 27356 27364 dst27358_02.B00 56 19.4 36.1 31.5
5627 -2250 27366 27380 dst27368_02.B00 130 13.6 25 43.8
5627 2250 27386 27499 dst27388_02.B00 1210 20.2 39.8 32.4
5735 -2250 26874 27068 dst26904_02.B00 1709 19.9 22.5 46.4
5735 2250 27069 27198 dst27070_02.B00 1509 15 34.6 32.9
5764 -2250 26468 26722 dst26489_02.B00 1189 10 25.2 44.3
5764 -2250 26776 26851 dst26779_02.B00 662 15.9 21.3 44

Table for Pions

I used the pion id code(both subroutines):

Josh's Pion cuts code

Beam Energy Torus Current Begin Run End Run file used events remaining after cuts # trig([math]10^6[/math]) expected # evts([math]10^6[/math])
first(%) second(%)
1606 1500 25488 25559 dst25504_02.B00 96.8 99 60 3.2
1606 1500 25669 25732 dst25669_02.B00 98.1 98.9 226 10
1606 1500 25742 26221 dst25754_02.B00 13.4 22.8 3154 13.3
1606 -1500 26222 26359 dst26224_02.B00 11.3 15.3 703 13.1
1724 -1500 27644 27798 dst27649_02.B00 15.3 18.7 211 20
2288 1500 27205 27351 dst27225_02.B00 16.4 18.9 1647 16.1
2562 -1500 27799 27924 dst27809_02.B00 11.1 14.2 1441 13.1
2562 -1500 27942 27995 dst27942_02.B00 11.1 14.2 841 32.3
2562 1500 28001 28069 dst28002_02.B00 22.4 23.1 1013 30.7
2792 -1500 27936 27941 dst27937_02.B00 12.3 15.4 69 20.6
4239 2250 28074 28277 dst28075_02.B00 16.7 14.3 2278 19.6
4239 -2250 28280 28479 dst28281_02.B00 10.4 12.6 2620 15.2
4239 2250 28506 28510 dst28509_02.B00 % % 75 18.1
5627 2250 27356 27364 dst27358_02.B00 40.5 40.8 56 19.4
5627 -2250 27366 27380 dst27368_02.B00 9.7 12.7 130 13.6
5627 2250 27386 27499 dst27388_02.B00 14.1 15.5 1210 20.2
5735 -2250 26874 27068 dst26904_02.B00 12.1 14.5 1709 19.9
5735 2250 27069 27198 dst27070_02.B00 19.5 22.9 1509 15
5764 -2250 26468 26722 dst26489_02.B00 9.6 13.3 1189 10
5764 -2250 26776 26851 dst26779_02.B00 10.3 13.9 662 15.9

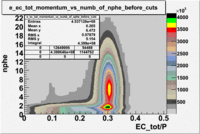
Plot of EC_tot/P vs nphe for Pions

E total vs nphe pions file dst27070.gif E total vs nphe electrons file dst27070.gif


Pi ec tot momentum vs nphe file dst27095 without cuts.gif Pi ec tot momentum vs nphe file dst27095 with cuts.gif

For Pions

EC tot P vs nphe for pions all data without cuts 2.gifEC tot P vs nphe for pions all data with cuts 2.gif


For Electrons

EC tot P vs nphe for electrons all data without cuts 2.gifEC tot P vs nphe for electrons all data with cuts 2.gif


OsiCuts Code

You use a subroutine called subr_osi( [parameters] ) as following. 

           osi_cut = subr_osi( particle_ptr[i].cc_sec,
                       particle_ptr[i].cc_status,
                       particle_ptr[i].cc_time,
                       particle_ptr[i].sc_time,
                       particle_ptr[i].trl1_phi,
                       particle_ptr[i].sc_r,
                       particle_ptr[i].cc_r,
                       particle_ptr[i].beta,
                       particle_ptr[i].sc_x,
                       particle_ptr[i].sc_y,
                       particle_ptr[i].sc_z,
                       particle_ptr[i].sc_cx,
                       particle_ptr[i].sc_cy,
                       particle_ptr[i].sc_cz,
                       dt_sc_cc,
                       proj_theta,
                       proj_phi,
                       int(torus)
                       );

OsiCuts

[Back to Analysis]

Retrieved from "https://wiki.iac.isu.edu/index.php?title=Particle_Identification&oldid=69447"