Analysis

Particle Identification
Quality Checks

EG1 run database
run summary
polarization info

Cuts

Calorimeter based cuts

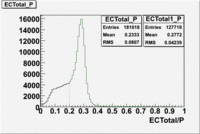
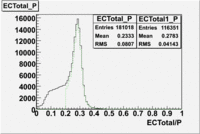
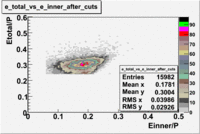
The distributions below represent two types of cuts applied to improve the electron particle identification (PID) using a 4 GeV electron beam incident on an NH3 target. The electron calorimeter is segmented into an inner[math]EC_{inner}[/math] and an outer[math]EC_{outer}[/math] region. The total energy absorbed by the calorimeter system is recorded in the variable [math]EC_{tot}[/math]. The momentum ([math]P[/math]) is calculated using the reconstructed track and the known torus magnetic field. The distributions of [math]EC_{tot}[/math] and [math]EC_{inner}[/math] are shown below where both have been divided by the electron momentum and no cuts have been applied.

[math]EC_{tot}\gt 0.2*p[/math]

Without any cuts we have 181018 entries. After using the following cut [math]EC_{tot}\gt 0.2*p[/math] we are getting 127719 entries, which is about 70.55% of 181018.

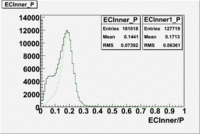
[math]EC_{inner}\gt 0.08*p[/math]

After the cut on the energy deposited into inner part of electron calorimeter, number of entries decreases by 22%.

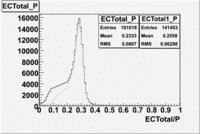
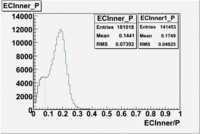
Both cuts [math] EC_{tot}\gt 0.2*p [/math] and [math] EC_{inner}\gt 0.08*p [/math]

In case of using the cuts of the total deposited energy and the energy deposited into inner calorimeter number of entries decreases ~36%

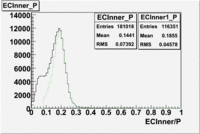
summary table

The "# of triggers" columns represents the number of events which generated a signal above threshold in the calorimeter and the scintillator. The expected # of events column represents the number of reconstructed events with tracks that also make it through the cuts defined in the table.

The semi-inclusive analysis will focus on the 4 GeV and 6 GeV data which have both inbending and outbending torus settings. Specifically runs 28074 - 28579 ( 4 GeV) and Runs 27356 - 27499 and 26874 - 27198 (6 GeV)

Beam Energy	Torus Current	Begin Run	End Run	file used	cuts			# trig([math]10^6[/math])	expected # evts([math]10^6[/math])	p<3,[math]EC_{tot}\gt 0.2*p [/math],[math] EC_{inner}\gt 0.08*p[/math](%)	p>3,[math]EC_{tot}\gt 0.24*p [/math],[math] EC_{inner}\gt 0.06*p[/math](%)
					[math]EC_{tot}\gt 0.2*p[/math]	[math]EC_{inner}\gt 0.08*p[/math]	[math]EC_{tot}\gt 0.2*p [/math] and [math] EC_{inner}\gt 0.08*p[/math]
1606	1500	25488	25559	dst25504_02.B00	64%	49.5%	78%	60	3.2
1606	1946	25560	25605			44
1606	1500	25669	25732	dst25669_02.B00	64%	49%	78%	226	10
1606	1500	25742	26221	dst25754_02.B00	21%	11%	24%	3154	13.3
1606	-1500	26222	26359	dst26224_02.B00	4.6%	3%	6.6%	703	13.1
1724	-1500	27644	27798	dst27649_02.B00	4.8%	2.2%	5.9%	211	20
1724	1500	28512	28526			159
1724	-1500	28527	28532			93
2288	1500	27205	27351	dst27225_02.B00	20.2%	13%	25.6%	1647	16.1
2562	-1500	27799	27924	dst27809_02.B00	5.7%	4.6%	8.6%	1441	13.1
2562	-1500	27942	27995	dst27942_02.B00	6.1%	4.4%	8.9%	841	32.3
2562	1500	28001	28069	dst28002_02.B00	27.8%	13%	29.6%	1013	30.7
2792	-1500	27936	27941	dst27937_02.B00	6.7%	5%	9.9%	69	20.6
3210	-2250	28549	28570			436
4239	2250	28074	28277	dst28075_02.B00	35.3%	23.9%	40.5%	2278	19.6
4239	-2250	28280	28479	dst28281_02.B00	9.1%	9.4%	13.6%	2620	15.2
4239	2250	28482	28494			7
4239	-2250	28500	28505			107
4239	2250	28506	28510	dst28509_02.B00	29.5%	22%	36%	75	18.1
5627	2250	27356	27364	dst27358_02.B00	33.2%	27.8%	41.3%	56	19.4	44.6	40.1
5627	-2250	27366	27380	dst27368_02.B00	12.6%	14.8%	19.5%	130	13.6	25.3	8.8
5627	2250	27386	27499	dst27388_02.B00	33.4%	27.8%	41.4%	1210	20.2	44.8	40.1
5627	965	27502	27617			493
5735	-2250	26874	27068	dst26904_02.B00	13%	15%	20%	1709	19.9	25.6	9.1
5735	2250	27069	27198	dst27070_02.B00	33.3%	28.8%	42.2%	1509	15	46	40.2
5764	-2250	26468	26722	dst26489_02.B00	12.2%	14.4%	19.1%	1189	10	24.6	9.3
5764	0	26723	26775			268
5764	-2250	26776	26851	dst26779_02.B00	13.5%	15.5%	20.5%	662	15.9	26.4	9.2

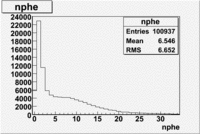
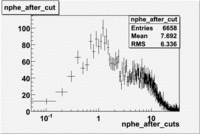
Cut on the number of photoelectrons

In this case is used a cut on the number of photoelectrons, which is [math]nphe\gt 2.5[/math]. The plots below show the effect of the number of photoelectrons cuts on the Cerenkov distribution. We see that after using cut the number of entries decreases ~40.7%

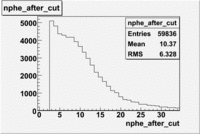
Used cuts [math]EC_{tot}\gt 0.24p[/math] and [math]EC_{inner}\gt 0.06p[/math]

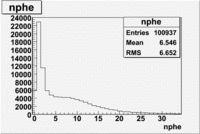
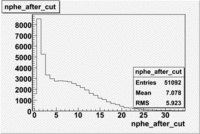
Used file dst28181_03(energy 4.2GeV). In this case was applied cuts on the polar angle([math]15\lt \theta\lt 20[/math]) and momentum([math]2.2\lt P\lt 2.6[/math]). Number of entries decreased by 96%(?????????????/)

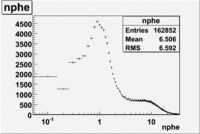
OSIPENKO cuts

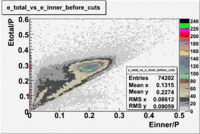
Plot of [math]EC_{tot}/p[/math] vs [math]EC_{inner}/p[/math]

In this case is used file dst27070(Energy 5.735 GeV and Torus 2250) and are applied the following EC cuts: For ECtotal - [math]EC_{tot}\gt 0.2p[/math], for EC inner - [math]EC_{inner}\gt 0.08p[/math].

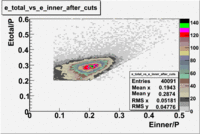
P<3

After using above cuts the number of entries decreases ~46%

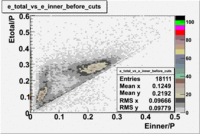
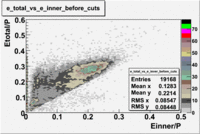
0.5<P<1

The number of entries decreased by ~51.8%

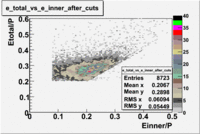
1<P<1.5

The number of entries decreased approximately by 47.8%

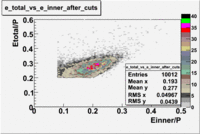
1.5<P<2

In this case the number of entries decreased by 46.1%

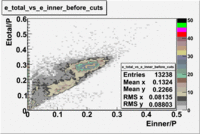
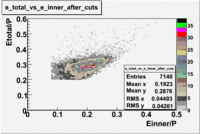
2<P<2.5

In this case the number of entries decreased by 38%

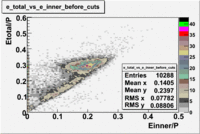
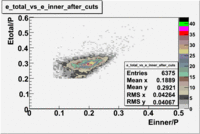
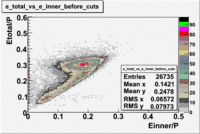
P>3

Used file dst27070(Energy 5.735 GeV and Torus 2250) and are applied the following EC cuts: For ECtotal - [math]EC_{tot}\gt 0.24p[/math], for EC inner - [math]EC_{inner}\gt 0.06p[/math].

The number of entries decreased by~40.2%

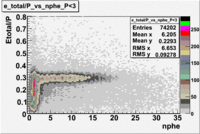
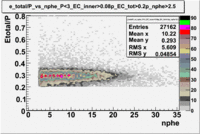
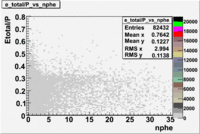
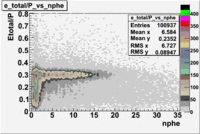
Plot of EC_tot/P vs nphe for Electrons

Used file dst27070(Energy 5.735 GeV and Torus 2250)

p<3 GeV

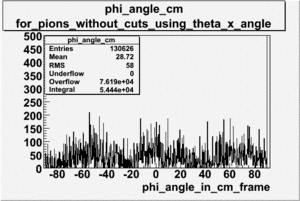
The graphs below represents all electron candidates having a momentum smaller than 3 GeV. Negatively charged pions are the most likely particle to be misidentified as an electrons by the tracking software. A negatively charged pion having a momentum of 3 GeV would generate less than ?? photons in the cerenkov counter. As a result the electron candidates which [math]n_{pe} \lt 1.xx [/math] are thought to be misidentified pions. The images which follow represent the effects of several cuts made for the purpose of removing misidentified particles.

chi_sqr for pions

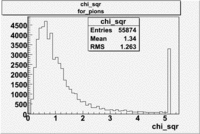
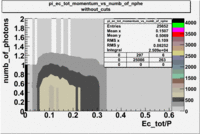
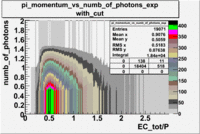
[math]\pi[/math]_Momentum_vs_Number_of_Photons for pions([math]\pi[/math])

Used file:27095_05.B00(energy=5.735GeV and torus=2250), everything is done for [math]\pi^-[/math]

p<3 GeV and [math]EC_{inner}\gt 0.08p[/math]

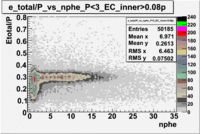
p<3 GeV, [math]EC_{inner}\gt 0.08p[/math] and [math]EC_{tot}\gt 0.2p[/math]

p<3 GeV, [math]EC_{inner}\gt 0.08p[/math], [math]EC_{tot}\gt 0.2p[/math] and nphe>2.5

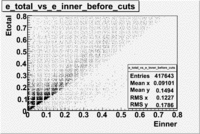
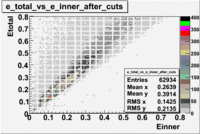
Plot of EC_total vs EC_inner

In this case file dst28181_03.B00 was used(Energy 4.2 GeV and Torus +2250). The following cuts were applied:[math]EC_{inner}\gt 0.005[/math], [math]EC_{tot}\gt 0.2*p[/math], ec_chi_sqr<0.1 and nphe>3.

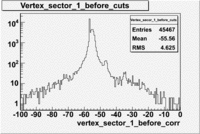
Raster and vertex correction

A raster calibration and a cut on the vertex distribution was made in order to select electrons from the polarized target, also the ones scattered from other materials in the beam path. A plot of the uncorrected vertex distribution is presented below for dst27070_02.B00 file(energy=5.7GeV Torus=2250)

Pion

Summary Table

Josh's Pion cuts code

Beam Energy	Torus Current	Begin Run	End Run	file used	# trig([math]10^6[/math])	expected # evts([math]10^6[/math])	p>3,[math]EC_{tot}\lt 0.2*p [/math],[math] EC_{inner}\lt 0.08*p[/math](%)	p<3,[math]EC_{tot}\lt 0.24*p [/math],[math] EC_{inner}\lt 0.06*p[/math](%)
1606	1500	25488	25559	dst25504_02.B00	60	3.2
1606	1500	25669	25732	dst25669_02.B00	226	10
1606	1500	25742	26221	dst25754_02.B00	3154	13.3
1606	-1500	26222	26359	dst26224_02.B00	703	13.1
1724	-1500	27644	27798	dst27649_02.B00	211	20
2288	1500	27205	27351	dst27225_02.B00	1647	16.1
2562	-1500	27799	27924	dst27809_02.B00	1441	13.1
2562	-1500	27942	27995	dst27942_02.B00	841	32.3
2562	1500	28001	28069	dst28002_02.B00	1013	30.7
2792	-1500	27936	27941	dst27937_02.B00	69	20.6
4239	2250	28074	28277	dst28075_02.B00	2278	19.6
4239	-2250	28280	28479	dst28281_02.B00	2620	15.2
4239	2250	28506	28510	dst28509_02.B00	75	18.1
5627	2250	27356	27364	dst27358_02.B00	56	19.4	36.1	31.5
5627	-2250	27366	27380	dst27368_02.B00	130	13.6	25	43.8
5627	2250	27386	27499	dst27388_02.B00	1210	20.2	39.8	32.4
5735	-2250	26874	27068	dst26904_02.B00	1709	19.9	22.5	46.4
5735	2250	27069	27198	dst27070_02.B00	1509	15	34.6	32.9
5764	-2250	26468	26722	dst26489_02.B00	1189	10	25.2	44.3
5764	-2250	26776	26851	dst26779_02.B00	662	15.9	21.3	44

Table for Pions

I used the pion id code(both subroutines):

Josh's Pion cuts code

Beam Energy	Torus Current	Begin Run	End Run	file used	events remaining after cuts		# trig([math]10^6[/math])	expected # evts([math]10^6[/math])
					first(%)	second(%)
1606	1500	25488	25559	dst25504_02.B00	96.8	99	60	3.2
1606	1500	25669	25732	dst25669_02.B00	98.1	98.9	226	10
1606	1500	25742	26221	dst25754_02.B00	13.4	22.8	3154	13.3
1606	-1500	26222	26359	dst26224_02.B00	11.3	15.3	703	13.1
1724	-1500	27644	27798	dst27649_02.B00	15.3	18.7	211	20
2288	1500	27205	27351	dst27225_02.B00	16.4	18.9	1647	16.1
2562	-1500	27799	27924	dst27809_02.B00	11.1	14.2	1441	13.1
2562	-1500	27942	27995	dst27942_02.B00	11.1	14.2	841	32.3
2562	1500	28001	28069	dst28002_02.B00	22.4	23.1	1013	30.7
2792	-1500	27936	27941	dst27937_02.B00	12.3	15.4	69	20.6
4239	2250	28074	28277	dst28075_02.B00	16.7	14.3	2278	19.6
4239	-2250	28280	28479	dst28281_02.B00	10.4	12.6	2620	15.2
4239	2250	28506	28510	dst28509_02.B00	%	%	75	18.1
5627	2250	27356	27364	dst27358_02.B00	40.5	40.8	56	19.4
5627	-2250	27366	27380	dst27368_02.B00	9.7	12.7	130	13.6
5627	2250	27386	27499	dst27388_02.B00	14.1	15.5	1210	20.2
5735	-2250	26874	27068	dst26904_02.B00	12.1	14.5	1709	19.9
5735	2250	27069	27198	dst27070_02.B00	19.5	22.9	1509	15
5764	-2250	26468	26722	dst26489_02.B00	9.6	13.3	1189	10
5764	-2250	26776	26851	dst26779_02.B00	10.3	13.9	662	15.9

Plot of EC_tot/P vs nphe for Pions

Quality Checks

Run Summary Table

The table below uses a characteristic DST file to try and estimate the sample size for a semi-inclusive analysis of pion electroproduction. The column marked "cuts" below indicates the number of events kept when the standard EC based electron identification cuts, described above, are used: [math]EC_{tot}\gt 0.2*p [/math] and
[math] EC_{inner}\gt 0.08*p[/math]. The next step will be to compare unpolarized pion production rates in order to evaluate the CLAS detectors efficiencies for measuring charged pions with different torus polarities. The question is whether you get the same rates for negatively charged pions in one torus polarity to positively charged pions using the opposite torus polarity.

Beam Energy	Torus Current	Target	Begin Run	End Run	file used	# trig([math]10^6[/math])	events remaining after [math]e^-[/math] cuts(%)	expected # evts([math]10^6[/math])	events remaining after [math]e^-[/math] and [math]\pi^+[/math] cuts(%)	expected # evts([math]10^6[/math])	events remaining after [math]e^-[/math] and [math]\pi^-[/math] cuts(%)	expected # evts([math]10^6[/math])
4239	2250	NH3	28205	28277	/cache/mss/home/nguler/dst/dst28205_05.B00	1108.72	60.8	674.1	8.3	92.02	3.24	35.92
		ND3	28074	28190	/cache/mss/home/nguler/dst/dst28187_05.B00	1117.87	59.6	666.25	7.99	89.32	3.3	36.9
	-2250	NH3	28407	28479	/cache/mss/home/nguler/dst/dst28409_05.B00	1013.57	24.2	245.28	0.12	1.22	0	0
		ND3	28278	28403	/cache/mss/home/nguler/dst/dst28400_05.B00	1556.04	23.9	371.89	0.02	0.31	0.05	0.51
5735	2250	NH3	27074	27195	/cache/mss/home/nguler/dst/dst27095_05.B00	1442.25	57.7	832.18	9.3	134.13	3.8	59.13
		ND3	27116	27170	/cache/mss/home/nguler/dst/dst27141_05.B00	624.55	59.1	369.10	9.53	59.52	3.9	24.36
	-2250	NH3	26911	27015	/cache/mss/home/nguler/dst/dst26988.B00	900.93	80.7	727.05	7.14	64.33	9.9	89.19
		ND3	27022	27068	/cache/mss/home/nguler/dst/dst27055_05.B00	711.53	80	569.22	6.97	49.59	10.1	71.86

Rates

Unpolarized Pion electroproduction

Rates from other experiments in our Kinematic range

Center of Mass Frame Transformation

We have proton and electron. In the Lab frame electron is moving along the x-axis with momentum ;[math]\vec{p_e}[/math] and proton is at rest. The 4-vectors are:

Lab Frame

[math]P_e=[/math]([math]E_e[/math],[math]p_e[/math],0,0) and for proton :[math]P_p=[/math]([math]m_p[/math],0,0,0)

CM Frame

:[math]{P_e}^{\prime}=[/math]([math]{E_e}^{\prime}[/math],[math]{p_e}^{\prime}[/math],[math]0[/math],[math]0[/math]) and for proton :[math]{P_p}^{\prime}=[/math]([math]{E_p}^{\prime}[/math],[math]{p_p}^{\prime}[/math],[math]0[/math],[math]0[/math])

Find [math] \beta_{CM} [/math] such that [math]P_{tot}^{CM}=0 =p_e^{\prime} + {p_p}^{\prime}[/math]

[math]\left ( \begin{matrix} {E_e}^{\prime} \\ p_e^{\prime} \\ 0 \\ 0 \end{matrix} \right )= \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 & 1 \end{matrix} \right ] \left ( \begin{matrix} E_e \\ p_e \\ 0 \\ 0 \end{matrix} \right )[/math]

[math]\left ( \begin{matrix} {E_p}^{\prime} \\ p_p^{\prime} \\ 0 \\ 0 \end{matrix} \right )= \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} m_p \\ 0 \\ 0 \\ 0 \end{matrix} \right )[/math]

Using the last two equations we will get the following for x component:

[math]{p_e}^{\prime}=-\gamma_{cm}(\beta_{cm} E_e-p_e)[/math]

[math]p_p^{\prime} = - \gamma_{cm} \beta_{cm} m_p[/math]

[math] \gamma_{cm}(p_e - \beta_{cm} E_e)= \gamma_{cm} \beta_{cm} m_p [/math]

[math]\beta_{cm} = \frac {p_e}{m_p + E_e}[/math]

Example of the Missing Mass Calculation for the following reaction [math]e^- p^+ \rightarrow (e^-)^{\prime} \pi^{-} X [/math]

[math]p_e = 5.736 Gev \sim E_e[/math] : electron mass is neglibible

[math]m_p = 0.938 GeV[/math] : Mass of a proton

[math]\beta_{cm} = \frac{5.736}{6.674} = 0.859 \lt 1[/math]

[math]\gamma_{cm} = \frac{1}{\sqrt{1 - \beta_{cm}^2}} = \frac{1}{\sqrt{1 - 0.859^2}} = 1.9532[/math]

[math]\left ( \begin{matrix} {E_e}^{\prime} \\ p_{ex}^{\prime} \\ p_{ey}^{\prime} \\ p_{ez}^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma_{cm} & 0 & 0 & -\gamma_{cm} \beta_{cm} \\ 0 & 1 &0 &0 \\ 0 &0 &1 &0 \\ -\gamma_{cm} \beta_{cm} &0 &0 &\gamma_{cm}\end{matrix} \right ] \left ( \begin{matrix} E_e=4.4915 \\ -0.549 \\ 0.974 \\ 4.3501 \end{matrix} \right )[/math]

[math]\left ( \begin{matrix} {E_p}^{\prime} \\ p_{px}^{\prime} \\ p_{py}^{\prime} \\ p_{pz}^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma_{cm} & 0 & 0 & -\gamma_{cm} \beta_{cm} \\ 0 & 1 &0 &0 \\ 0 &0 &1 &0 \\ -\gamma_{cm} \beta_{cm} &0 &0 & \gamma_{cm} \end{matrix} \right ] \left ( \begin{matrix} E_p = 1.4563 \\ 0.3697 \\ -0.3447 \\ 0.9924 \end{matrix} \right )[/math]

[math]\left ( \begin{matrix} {E_{\pi^-}}^{\prime} \\ p_{\pi^- x}^{\prime} \\ p_{{\pi^-} y}^{\prime} \\ p_{{\pi^-} z}^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma_{cm} & 0 & 0 & -\gamma_{cm} \beta_{cm} \\ 0 & 1 &0 &0 \\ 0 &0 &1 &0 \\ -\gamma_{cm} \beta_{cm} &0 &0 & \gamma_{cm} \end{matrix} \right ] \left ( \begin{matrix} E_{\pi^-} = 0.5757 \\ 0.1052 \\ -0.4394 \\ 0.3282 \end{matrix} \right )[/math]

Electron

[math]\left ( \begin{matrix} {E_e}^{\prime} \\ p_{ex}^{\prime} \\ p_{ey}^{\prime} \\ p_{ez}^{\prime} \end{matrix} \right )= \left ( \begin{matrix} 4.4915 \gamma_{cm} - 4.3501 \gamma_{cm} \beta_{cm} \\ -0.549 \\ 0.974 \\ -4.4915 \gamma_{cm} \beta_{cm} + 4.3501 \gamma_{cm} \end{matrix} \right ) = \left ( \begin{matrix} 1.4742 \\ -0.549 \\ 0.974 \\ 0.96078 \end{matrix} \right )[/math]

Proton

[math]\left ( \begin{matrix} {E_p}^{\prime} \\ p_{px}^{\prime} \\ p_{py}^{\prime} \\ p_{pz}^{\prime} \end{matrix} \right )= \left ( \begin{matrix} 1.4563\gamma_{cm} - 0.9924 \gamma_{cm} \beta_{cm} \\ 0.3697 \\ -0.3447 \\-1.4563 \gamma_{cm} \beta_{cm} + 0.9924\gamma_{cm} \end{matrix} \right ) = \left ( \begin{matrix} 1.17939 \\ 0.3697 \\ -0.3447 \\ -0.505023 \end{matrix} \right )[/math]

[math]\pi^-[/math]

[math]\left ( \begin{matrix} {E_{\pi^-}}^{\prime} \\ p_{\pi^- x}^{\prime} \\ p_{{\pi^-} y}^{\prime} \\ p_{{\pi^-} z}^{\prime} \end{matrix} \right )= \left ( \begin{matrix} 0.5757\gamma_{cm} - 0.3282 \gamma_{cm} \beta_{cm} \\ 0.1052 \\ -0.4394 \\ -0.5757 \gamma_{cm} \beta_{cm} + 0.3282\gamma_{cm} \end{matrix} \right ) = \left ( \begin{matrix} 0.5738 \\ 0.1052 \\ -0.4394 \\ -0.324868 \end{matrix} \right )[/math]

[math]\vec {P_{tot}}^{\prime} = (p_{ex}^{\prime} + p_{px}^{\prime} + p_{\pi^-x}^{\prime})\hat{x} + (p_{ey}^{\prime} + p_{py}^{\prime} + p_{\pi^-y}^{\prime})\hat{y} + (p_{ez}^{\prime} + p_{pz}^{\prime} + p_{\pi^-z}^{\prime})\hat{z} = - 0.0741 \hat{x} + 0.1899 \hat{y} + 0.13 \hat{z} [/math]

Missing Mass

Conservation of the 4-momentum gives us following

[math](P_e)^\mu + (P_p)^\mu = ({P_e}^{\prime})^\mu + ({P_X}^{\prime})^\mu + ({P_{\pi^-}}^{\prime})^\mu[/math]
[math](P_e)_\mu + (P_p)_\mu = ({P_e}^{\prime})_\mu + ({P_X}^{\prime})_\mu + ({P_{\pi^-}}^{\prime})_\mu[/math]

Solving it for the final proton state

[math]{M_x}^2 = ({P_X}^{\prime})_\mu({P_X}^{\prime})^\mu = [(P_e)_\mu + (P_p)_\mu - ({P_e}^{\prime})_\mu - ({P_{\pi^-}}^{\prime})_\mu][(P_e)^\mu + (P_p)^\mu - ({P_e}^{\prime})^\mu - ({P_{\pi^-}}^{\prime})^\mu][/math]

In our case 4-vectors for particles are

[math](P_e)_\mu = ( 5.736, 0, 0, 5.736 GeV)[/math]
[math](P_p)_\mu = (m_p, 0, 0, 0)[/math]
[math]({P_e}^{\prime})_\mu = (4.4914861, -0.549, 0.974, 4.3501 )[/math]
[math]({P_{\pi^-}}^{\prime})_\mu = (0.575721, 0.1052, -0.4394, 0.3282)[/math]

Plug and chug

[math]{M_x}^2 = [( 5.736, 0, 0, 5.736 GeV) + ( m_p, 0, 0, 0 ) - (4.4914861, -0.549, 0.974, 4.3501 ) - (0.575721, 0.1052, -0.4394, 0.3282)[/math]] [[math]\left (\begin{matrix} 5.736 \\ 0 \\ 0 \\ 5.736 \end{matrix} \right )[/math] + [math]\left (\begin{matrix} m_p \\ 0 \\ 0 \\ 0 \end{matrix} \right) [/math] - [math]\left (\begin{matrix} 4.4914861 \\ -0.549 \\ 0.974 \\ 4.3501 \end{matrix} \right) [/math] - [math]\left ( \begin{matrix}0.575721 \\ 0.1052 \\ -0.4394 \\ 0.3282 \end{matrix} \right) ] = 0.981198614 GeV^2[/math]

[math]M_x = 0.9905547 GeV[/math]

Example of the Missing Mass Calculation for the following reaction [math]\vec{e}p \rightarrow (e^-)^{\prime} n \pi^+[/math]

Used file dst27095_05.B00. Target [math]NH_3[/math], Beam Energy 5.735 GeV and Torus Current +2250. Event_number=3106861

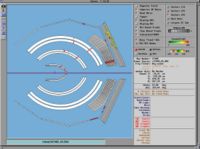
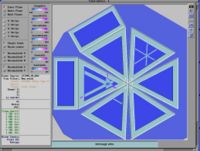
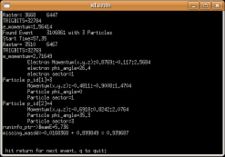
[math]p_e = 5.736 Gev \sim E_e[/math] : electron mass is negligible

[math]m_p = 0.938 GeV[/math] : Mass of a proton

[math]m_n = 0.939566 GeV[/math] : Mass of a neutron

[math]\beta_{cm} = \frac{5.736}{6.674} = 0.859 \lt 1[/math]

[math]\gamma_{cm} = \frac{1}{\sqrt{1 - \beta_{cm}^2}} = \frac{1}{\sqrt{1 - 0.859^2}} = 1.9559[/math]

[math]\left ( \begin{matrix} {E_e}^{\prime} \\ p_{ex}^{\prime} \\ p_{ey}^{\prime} \\ p_{ez}^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma_{cm} & 0 & 0 & -\gamma_{cm} \beta_{cm} \\ 0 & 1 &0 &0 \\ 0 &0 &1 &0 \\ -\gamma_{cm} \beta_{cm} &0 &0 &\gamma_{cm}\end{matrix} \right ] \left ( \begin{matrix} E_e=2.7165 \\ 0.8769 \\ -0.117 \\ 2.5684 \end{matrix} \right )[/math]

[math]\left ( \begin{matrix} {E_n}^{\prime} \\ p_{nx}^{\prime} \\ p_{ny}^{\prime} \\ p_{nz}^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma_{cm} & 0 & 0 & -\gamma_{cm} \beta_{cm} \\ 0 & 1 &0 &0 \\ 0 &0 &1 &0 \\ -\gamma_{cm} \beta_{cm} &0 &0 & \gamma_{cm} \end{matrix} \right ] \left ( \begin{matrix} E_n =2.0218 \\ -0.4811 \\ -0.9008 \\ 1.4704 \end{matrix} \right )[/math]

[math]\left ( \begin{matrix} {E_{\pi^+}}^{\prime} \\ p_{\pi^+ x}^{\prime} \\ p_{{\pi^+} y}^{\prime} \\ p_{{\pi^+} z}^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma_{cm} & 0 & 0 & -\gamma_{cm} \beta_{cm} \\ 0 & 1 &0 &0 \\ 0 &0 &1 &0 \\ -\gamma_{cm} \beta_{cm} &0 &0 & \gamma_{cm} \end{matrix} \right ] \left ( \begin{matrix} E_{\pi^+} =2.3431 \\ -0.6918 \\ 0.8242 \\ 2.0764 \end{matrix} \right )[/math]

Electron

[math]\left ( \begin{matrix} {E_e}^{\prime} \\ p_{ex}^{\prime} \\ p_{ey}^{\prime} \\ p_{ez}^{\prime} \end{matrix} \right )= \left ( \begin{matrix} 2.7165 \gamma_{cm} - 2.5684 \gamma_{cm} \beta_{cm} \\ 0.8769 \\ -0.117 \\ -2.7165\gamma_{cm} \beta_{cm} + 2.5684 \gamma_{cm} \end{matrix} \right ) = \left ( \begin{matrix} 0.99569 \\ 0.8769 \\ -0.117 \\ 0.45728 \end{matrix} \right )[/math]

Neutron

[math]\left ( \begin{matrix} {E_n}^{\prime} \\ p_{nx}^{\prime} \\ p_{ny}^{\prime} \\ p_{nz}^{\prime} \end{matrix} \right )= \left ( \begin{matrix} 2.0218\gamma_{cm} - 1.4704 \gamma_{cm} \beta_{cm} \\ -0.4811 \\ -0.9008 \\-2.0218 \gamma_{cm} \beta_{cm} + 1.4704\gamma_{cm} \end{matrix} \right ) = \left ( \begin{matrix} 1.4828 \\ -0.4811 \\ -0.9008 \\ -0.52256 \end{matrix} \right )[/math]

[math]\pi^+[/math]

[math]\left ( \begin{matrix} {E_{\pi^+}}^{\prime} \\ p_{\pi^+ x}^{\prime} \\ p_{{\pi^+} y}^{\prime} \\ p_{{\pi^+} z}^{\prime} \end{matrix} \right )= \left ( \begin{matrix} 2.3431\gamma_{cm} - 2.0764 \gamma_{cm} \beta_{cm} \\ -0.6918 \\ 0.8242 \\ -2.3431 \gamma_{cm} \beta_{cm} + 2.0764\gamma_{cm} \end{matrix} \right ) = \left ( \begin{matrix} 1.09257 \\ -0.6918 \\ 0.8242 \\ 0.1226 \end{matrix} \right )[/math]

[math]\vec {P_{tot}}^{\prime} = (p_{ex}^{\prime} + p_{nx}^{\prime} + p_{\pi^+x}^{\prime})\hat{x} + (p_{ey}^{\prime} + p_{ny}^{\prime} + p_{\pi^+y}^{\prime})\hat{y} + (p_{ez}^{\prime} + p_{nz}^{\prime} + p_{\pi^+z}^{\prime})\hat{z} = -0.296 \hat{x} + -0.1936 \hat{y} + 0.0573 \hat{z} [/math]

Missing Mass Calculation

Below is the conservation of the 4-momentum

[math](P_e)^\mu + (P_p)^\mu = ({P_e}^{\prime})^\mu + ({P_X}^{\prime})^\mu + ({P_{\pi^+}}^{\prime})^\mu[/math]
[math](P_e)_\mu + (P_p)_\mu = ({P_e}^{\prime})_\mu + ({P_X}^{\prime})_\mu + ({P_{\pi^+}}^{\prime})_\mu[/math]

Solving it for the final neutron state

[math]{M_x}^2 = ({P_X}^{\prime})_\mu({P_X}^{\prime})^\mu = [(P_e)_\mu + (P_p)_\mu - ({P_e}^{\prime})_\mu - ({P_{\pi^+}}^{\prime})_\mu][(P_e)^\mu + (P_p)^\mu - ({P_e}^{\prime})^\mu - ({P_{\pi^+}}^{\prime})^\mu][/math]

The 4-vectors for the particles in this event

[math](P_e)_\mu = ( 5.736, 0, 0, 5.736 GeV)[/math]
[math](P_p)_\mu = (m_p, 0, 0, 0)[/math]
[math]({P_e}^{\prime})_\mu = (2.7164, 0.8769, -0.117, 2.5684 )[/math]
[math]({P_{\pi^+}}^{\prime})_\mu = (2.3431, -0.6918, 0.8242, 2.0764)[/math]

[math]{M_x}^2 = [( 5.736, 0, 0, 5.736 GeV) + ( m_p, 0, 0, 0 ) - ( 2.7164, 0.8769, -0.117, 2.5684 ) - ( 2.3431, -0.6918, 0.8242, 2.0764 )[/math]] [[math]\left (\begin{matrix} 5.736 \\ 0 \\ 0 \\ 5.736 \end{matrix} \right )[/math] + [math]\left (\begin{matrix} m_p \\ 0 \\ 0 \\ 0 \end{matrix} \right) [/math] - [math]\left (\begin{matrix} 2.7164 \\ 0.8769 \\ -0.117 \\ 2.5684 \end{matrix} \right) [/math] - [math]\left ( \begin{matrix} 2.3431 \\ -0.6918 \\ 0.8242 \\ 2.0764\end{matrix} \right) ] = 0.882724889 GeV^2[/math]

[math]M_x = 0.9395344 GeV[/math]

[math]\phi_{diff}^{LAB} = \phi_e^{LAB} - \phi_{\pi^+}^{LAB} = (120 + 35.3) -26.4 = 128.9[/math]

[math]{\phi_{\pi}}^{CM}[/math] transformation from LAB frame to CM frame

Used file dst27095_05, event_number=3106861

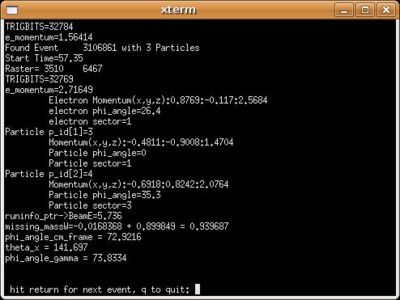
[math]\beta_{cm} = \frac{5.736}{6.674} = 0.859 \lt 1[/math]

[math]\gamma_{cm} = \frac{1}{\sqrt{1 - \beta_{cm}^2}} = \frac{1}{\sqrt{1 - 0.859^2}} = 1.9559[/math]

[math]E_e = \sqrt{{p_e}^2 + {m_e}^2} = \sqrt{0.8769^2 + 0.117^2 + 2.56842^2} = 2.7165[/math]

Calculation of [math]{{\phi}_{\gamma}}^{CM}[/math]

[math]{\phi_{\gamma}}^{CM} = tan^{-1}(\frac{{p_{e z}}^{CM}}{{p_{e z}}^{ CM \prime}})[/math]

[math]{p_{e z}}^{CM} = -\gamma_{CM} \beta_{CM}{p_{e z}}^{LAB} + \gamma_{CM} {p_{e z}}^{LAB} = [/math]

[math] = -1.9559 \times 0.8594 \times 5.736 + 1.9559 \times 5.736 = 1.5773 [/math]

[math]{p_{e z}}^{CM \prime} = -\gamma_{CM} \beta_{CM} E_e + \gamma_{CM} {p_{e z}}^{LAB \prime} = [/math]

[math]= -1.9559 \times 0.8594 \times 2.7165 + 1.9559 \times 2.5684 = 0.4574 [/math]

[math]\phi_{\gamma} = tan^{-1}(\frac{1.5773}{0.4574}) = 73.83 [/math]

Calculation of [math]{\theta_x}^{CM}[/math]

[math]{\theta_x}^{CM} = cos^{-1}(\frac{p_{e z}^{CM \prime} - {p_{e z}}^{CM}}{\sqrt{{p_{e x}^{CM \prime}}^2 + {p_{e y}^{CM \prime}}^2 + ({p_{e z}^{CM \prime} - {p_{e z}}^{CM}})^2}}) = [/math]

[math] = cos^{-1}(\frac{0.4574 - 1.5773}{\sqrt{0.8769^2 + (-0.117)^2 + (0.4574 - 1.5773)^2}}) = 141.69 [/math]

Calculation of [math]{\phi_{\pi}}^{CM}[/math]

[math]E_{\pi} = \sqrt{{p_{\pi}}^2 + {m_{\pi}}^2} = [/math]

[math] = \sqrt{(-0.6918)^2 + 0.8242^2 + 2.0764^2 + 0.13969^2} = 2.3428 [/math]

[math]{p_{\pi z}}^{CM} = -\gamma_{CM} \beta_{CM} E_{\pi} + \gamma_{CM} {p_{\pi z}}^{LAB} = [/math]

[math]= -1.9559 \times 0.8594 \times 2.3428 + 1.9559 \times 2.0764 = 0.1232 [/math]

[math]{\phi}_{\pi}^{CM} = tan^{-1}(\frac{{p_{\pi y}}^{CM \prime}}{{p_{\pi x}}^{CM \prime}}) = [/math]

[math] = tan^{-1}(\frac{-sin{{\phi}_{\gamma}} \times p_{\pi x}^{CM} + cos{{\phi}_{\gamma}} \times p_{\pi y}^{CM}}{sin{\theta_x}\times(cos{{\phi}_{\gamma}} \times p_{\pi x}^{CM} + sin{{\phi}_{\gamma}} \times p_{\pi y}^{CM}) + cos{\theta_x} \times p_{\pi z}^{CM}}) = [/math]

[math] = tan^{-1}(\frac{-sin(73.83) \times (-0.6918) + cos(73.83) \times 0.8242}{sin(141.69)\times(cos(73.83) \times (-0.6918) + sin(73.83) \times 0.8242) + cos(141.69) \times 0.1232} = 72.92 [/math]

Missing_Mass(experimental data)

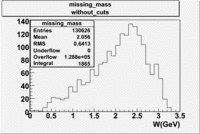
The mean value of the missing mass is around 2.056 GeV.

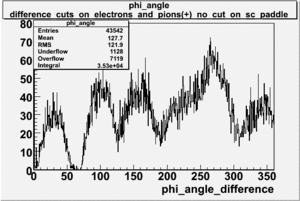
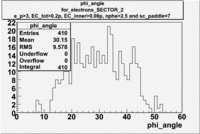
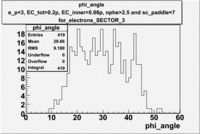
[math]\phi[/math] angle for electrons and pions ([math]\pi^+[/math]) in lab frame [math]\phi_{e^-}^{LAB}[/math], [math]\phi_{\pi^+}^{LAB}[/math]

Used file is dst27095_05.B00.Target material is [math]NH_3[/math], Torus +2250 and beam energy 5.7 GeV

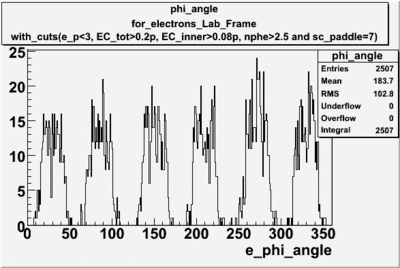
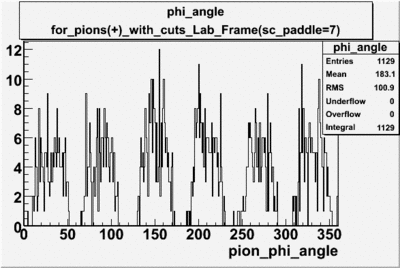
For Electrons [math]e^-[/math] with cuts (e_p<3, [math]EC_{tot}\gt 0.2p[/math], [math]EC_{inner}\gt 0.08p[/math], nphe>2.5 and sc_paddle=7)	For Pions([math]\pi^+[/math]) with cuts for sc_paddle=7

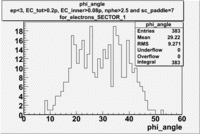
For Electrons with cuts (e_p<3, [math]EC_{tot}\gt 0.2p[/math], [math]EC_{inner}\gt 0.08p[/math], nphe>2.5 and sc_paddle=7)
SECTOR 1	SECTOR 2	SECTOR 3
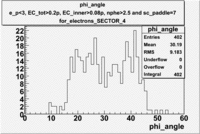
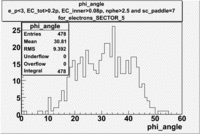
SECTOR 4	SECTOR 5	SECTOR 6

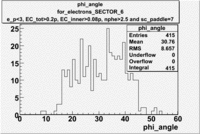
For pions([math]\pi^+[/math]) with cuts for sc_paddle=7
SECTOR 1	SECTOR 2	SECTOR 3
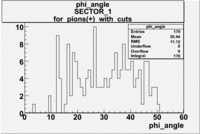
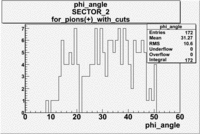
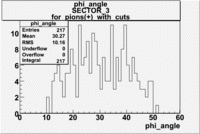
SECTOR 4	SECTOR 5	SECTOR 6

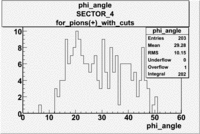
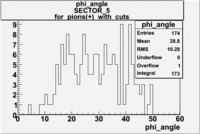
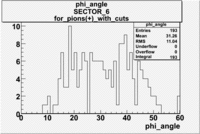
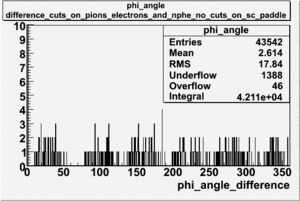
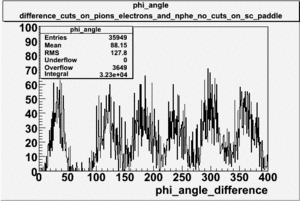
The plots below show what happens when you require the nphe from electron to be > 2.5 and you only look for pions in scintillator paddle 7.

Why is there a big  gap for[math] \phi \lt  100[/math] ? 

Take a look at theta -vs- phi plots for each sector.  Do the dead spots impact difference?

Write equation for[math] \phi_{\pi}^{CM}[/math] in terms of Lab frame Momentum and energy.

Graph [math]\phi_{\pi}^{CM}[/math] for Pions hitting paddle #7.  The y-axis should be pion counting rate in units of pions per nanCoulomb.

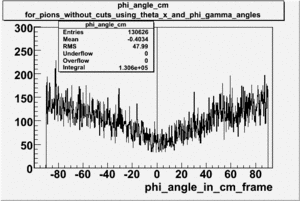
[math]\phi[/math] angle in the Center of Mass Frame

The variables below are in Lab Frame:

From [math]\vec{e}p \rightarrow n \pi^+[/math] from CLAS

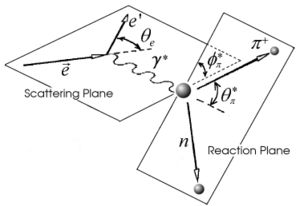Kinematics of single [math]\pi^+[/math] electroproduction

From the above picture we can write down the momentum x,y and z components for pion in terms of angle and total momentum.

[math]{p_{\pi x}}^{LAB} = p_{\pi}^{LAB} {sin {\theta}}_{\pi}^{LAB} cos {\phi}_{\pi}^{LAB}[/math]

[math]{p_{\pi y}}^{LAB} = p_{pi}^{LAB} {sin {\theta}}_{\pi}^{LAB} sin {\phi}_{\pi}^{LAB}[/math]

[math]{\phi}_{\pi}^{LAB} = arctg(\frac{{p_{\pi y}}^{LAB}}{{p_{\pi x}}^{LAB}})[/math]

where [math]{p_{\pi x}}^{LAB}[/math] and [math]{p_{\pi y}}^{LAB}[/math] are the x and y components of the pion momentum.

[math](P_e)^{\mu}[/math] - Initial electron 4-momentum
[math](P_N)^{\mu}[/math] - Target Nucleon 4-momentum
[math](P_e^{\prime})^{ \mu}[/math] - Scattered electron 4-momentum
[math](P_h)^{\mu}[/math] - Hadron final state 4-momentum
[math](P_m)^{\mu}[/math] - Meson final state 4-momentum

[math]h=n[/math], [math]m=\pi^+[/math] for [math]\vec{e} (\vec{p},\vec{e}^{\prime}) \pi^+ n[/math]

In Inclusive [math]\vec{e} (\vec{p},\vec{e}^{\prime}) X [/math]

Then The Missing Mass [math]W = (E_x ^2 - p_x ^2)[/math]

In Exclusive [math]\vec{e} (\vec{p},\vec{e}^{\prime}) \pi^+ X[/math]

Then Missing Mass [math] M = (E_h ^2 - p_h ^2)[/math]

Conservation of 4-momentum gives

[math](P_e)^\mu + (P_N)^\mu = ({P_e}^{\prime})^\mu + {P_h}^\mu + ({P_m})^\mu[/math]

[math]{P_h}^\mu = (P_e)^\mu - ({P_e}^{\prime})^\mu + (P_N)^\mu -({P_m})^\mu[/math]

[math]q^\mu[/math] - 4-momentum of the exchanged virtual photon([math]\gamma[/math])

[math]q^\mu = (P_e^{\prime})^\mu - P_e ^{\mu} = (E_e ^{\prime}, {\vec{p}_e} ^{\prime}) - (E_e, {\vec{p}_e}) = [/math]

[math] = (E_e ^{\prime} - E_e,{\vec{p}_e} ^{\prime} - {\vec{p}_e} ) = (0,{\vec{p}_e} ^{\prime} - {\vec{p}_e}) = (0, p_{e,x}^{\prime}\hat{x} + p_{e,y}^{\prime}\hat{y} + (p_{e,z}^{\prime} - p_{e,z})\hat{z})[/math]

[math]\phi_{\gamma} = tan^{-1}(\frac{p_{e x}^{\prime}}{p_{e z}^{\prime}})[/math]

[math]\theta_x = cos^{-1}(\frac{p_{e z}^{\prime} - p_{e z}}{\sqrt{{p_{e x}^{\prime}}^2 + {p_{e y}^{\prime}}^2 + ({p_{e z}^{\prime} - p_{e z}})^2}})[/math]

[math]p_{e x}^{\prime} = p_{e x}^{\prime CM}[/math]

[math]p_{e y}^{\prime} = p_{e y}^{\prime CM}[/math]

[math]p_{e z}^{\prime CM} = -E_e \gamma_{CM} \beta_{CM} + p_{e z }^{\prime LAB} \gamma_{CM}[/math]

[math]p_{e z}^{CM} = -p_{e z}^{LAB} \gamma_{CM} \beta_{CM} + p_{e z}^{LAB} \gamma_{CM}[/math]

[math]p_{e z}^{LAB} = Beam Energy [/math]

First the coordinate system is rotated around z-axis by [math]\phi_{\gamma}[/math] angle and then around y-axis by [math]\theta_x[/math] angle. Below is presented the transformation matrix.

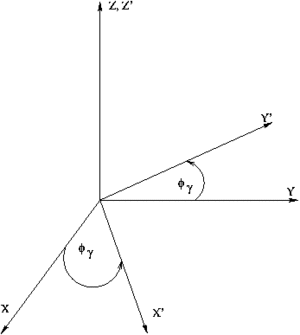
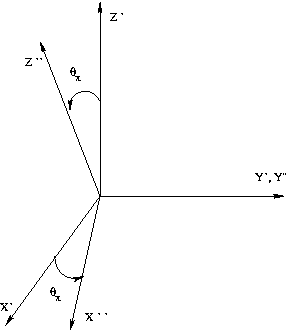
[math]\left ( \begin{matrix} p_{\pi x}^{LAB{\prime}} \\ p_{\pi y}^{LAB{\prime}} \\p_{\pi z}^{LAB{\prime}} \end{matrix} \right )= \left [ \begin{matrix} cos {\theta}_x & 0 & -sin {\theta_x} \\ 0 & 1 &0 \\ sin {\theta_x} &0 & cos {\theta_x} \end{matrix} \right ] \left [ \begin{matrix} cos {\phi_{\gamma}} & sin {\phi_{\gamma}} & 0 \\ -sin {\phi_{\gamma}} & cos {\phi_{\gamma}} &0 \\ 0 &0 & 1 \end{matrix} \right ] \left ( \begin{matrix} p_{\pi x}^{LAB} \\p_{\pi y}^{LAB} \\ p_{\pi z}^{LAB} \end{matrix} \right ) = [/math]

[math]= \left ( \begin{matrix} cos {\theta}_x (cos {\phi_{\gamma}} p_{\pi x}^{LAB} + sin {\phi_{\gamma}} p_{\pi y}^{LAB}) - sin {\theta}_x p_{\pi z}^{LAB} \\ -sin {\phi_{\gamma}} p_{\pi x}^{LAB} + cos {\phi_{\gamma}} p_{\pi y}^{LAB} \\ sin {\theta}_x (cos {\phi_{\gamma}} p_{\pi x}^{LAB} + sin {\phi_{\gamma}} p_{\pi y}^{LAB}) + cos {\theta}_x p_{\pi z}^{LAB} \end{matrix} \right ) [/math]

[math]{\phi}_{\pi}^{LAB{\prime}} = tan^{-1}(\frac{{p_{\pi y}}^{LAB{\prime}}}{{p_{\pi x}}^{LAB{\prime}}}) = tan^{-1}(\frac{-sin{\phi_{\gamma}} \times p_{\pi x}^{LAB} + cos{\phi_{\gamma}} \times p_{\pi y}^{LAB}}{sin{\theta_x}\times(cos{\phi_{\gamma}} \times p_{\pi x}^{LAB} + sin{\phi_{\gamma}} \times p_{\pi y}^{LAB}) + cos{\theta_x} \times p_{\pi z}^{LAB}})[/math]

[math]{\phi}_{\pi}^{CM} = tan^{-1}(\frac{{p_{\pi y}}^{CM}}{{p_{\pi x}}^{CM}}) = tan^{-1}(\frac{-sin{\phi_{\gamma}} \times p_{\pi x}^{CM} + cos{\phi_{\gamma}} \times p_{\pi y}^{CM}}{sin{\theta_x}\times(cos{\phi_{\gamma}} \times p_{\pi x}^{CM} + sin{\phi_{\gamma}} \times p_{\pi y}^{CM}) + cos{\theta_x} \times p_{\pi z}^{CM}})[/math]

[math]p_{\pi x}^{CM} = p_{\pi x}^{LAB}[/math]

[math]p_{\pi y}^{CM} = p_{\pi y}^{LAB}[/math]

[math]p_{\pi z}^{CM} = -E_{\pi} \gamma_{CM} \beta_{CM} + p_{\pi z}^{LAB} \gamma_{CM}[/math]

= Phi rate =

Why does the [math]\phi[/math] angle only go out to 80 degrees?

Add FC histogram, Add plot from paper,  start calculating cross -section, Find luminosity of NH3 target used

The rotation matrix, that rotates the coordinate system around y axis by [math]\theta_x[/math] angle is given

[math]\left ( \begin{matrix} p_{\pi x}^{LAB{\prime}} \\ p_{\pi y}^{LAB{\prime}} \\p_{\pi z}^{LAB{\prime}} \end{matrix} \right )= \left [ \begin{matrix} cos {\theta}_x & 0 & sin {\theta_x} \\ 0 & 1 &0 \\ -sin {\theta_x} &0 & cos {\theta_x} \end{matrix} \right ] \left ( \begin{matrix} p_{\pi x}^{LAB} \\p_{\pi y}^{LAB} \\ p_{\pi z}^{LAB} \end{matrix} \right )[/math]

Now, the x, y and z components of the momentum can be written in terms of the momentums of the rotated system.

[math]p_{\pi x}^{LAB {\prime}} = cos {\theta}_x \times p_{\pi x}^{LAB} + sin {\theta_x} \times p_{\pi z}^{LAB}[/math]

[math]p_{\pi y}^{LAB{\prime}} = p_{\pi y}^{LAB}[/math]

[math]p_{\pi z}^{LAB{\prime}} = -sin {\theta}_x \times p_{\pi x}^{LAB} + cos {\theta_x} \times p_{\pi z}^{LAB}[/math]

[math]{\phi}_{\pi}^{LAB} = arctg(\frac{p_{\pi y}^{LAB}}{cos {\theta}_x \times p_{\pi x}^{LAB} + sin {\theta_x} \times p_{\pi z}^{LAB}})[/math]

[math]{\phi}_{\pi}^{CM} = tan^{-1}(\frac{p_{\pi y}^{LAB}}{cos {\theta}_x \times p_{\pi x}^{LAB} + sin {\theta_x} \times (- \gamma_{CM} \beta_{CM} E_{\pi}^{LAB} + \gamma_{CM} p_{\pi z}^{LAB})})[/math]

where [math]\theta_x[/math] is the angle between the photon and the electron. The angle can be found using the conservation of momentum and energy.
Conservation of Momentum [math]\Rightarrow[/math] :

[math]\vec{p}_e = \vec{p}_{e^{\prime}} + \vec{p}_{\gamma}[/math] [math]\Rightarrow[/math] [math]\vec{p}_{e^{\prime}} = \vec{p}_e - \vec{p}_{\gamma}[/math]
[math]{p_{e^{\prime}}}^2 = {p_e}^2 - 2 p_e p_{\gamma}cos {\theta_x} + {p_{\gamma}}^2[/math]
[math]cos {\theta_x} = \frac {{p_e}^2 + {p_{\gamma}}^2 - {p_{e^{\prime}}}^2}{2 p_e p_{\gamma}}[/math]

Conservation of Energy [math]\Rightarrow[/math] :

[math] E_e = E_{e^{\prime}} + E_{\gamma}[/math]
[math]\sqrt {(m_e c^2)^2 + (p_e c)^2} = \sqrt {(m_e c^2)^2 + (p_{e^{\prime}} c)^2} + p_{\gamma} c[/math]
[math]p_{\gamma} c = \sqrt {(m_e c^2)^2 + (p_e c)^2} - \sqrt {(m_e c^2)^2 + (p_{e^{\prime}} c)^2}[/math]
[math]p_{\gamma} = \sqrt {(m_e)^2 + (p_e)^2} - \sqrt {(m_e)^2 + (p_{e^{\prime}})^2}[/math]

The [math]cos {\theta_x}[/math] can be written in the following way
[math]cos {\theta_x} = \frac {{p_e}^2 + ( \sqrt {(m_e)^2 + (p_e)^2} - \sqrt {(m_e)^2 + (p_{e^{\prime}})^2})^2 - {p_{e^{\prime}}}^2}{2 p_e ( \sqrt {(m_e)^2 + (p_e)^2} - \sqrt {(m_e)^2 + (p_{e^{\prime}})^2}) }[/math]

 angle is in degrees

Pion Rates -vs- Paddle for opposite sign Torus fields

using all events in which the first particle (the one which caused the trigger) is defined as an electrons and passes the

above electron cuts.

sc_paddle vs X_bjorken 5.7 GeV Beam Energy

no cuts	cuts	no cuts	cuts
Electrons	B > 0		B<0
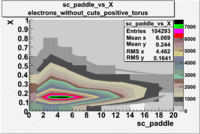
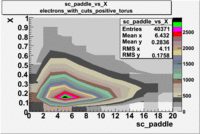
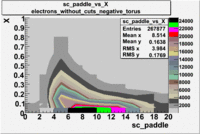
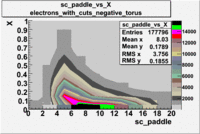
[math]\pi^-[/math]	B > 0		B<0
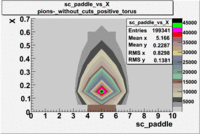
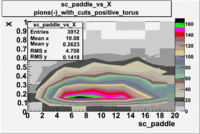
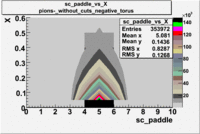
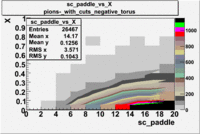
[math]\pi^+[/math]	B > 0		B<0

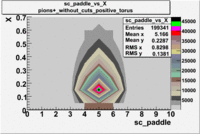
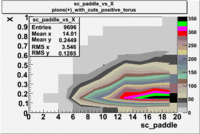
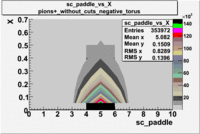
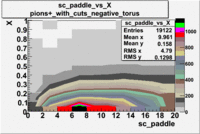
sc_paddle vs X_bjorken with cuts 5.7 GeV Beam Energy(number of events=2)

[math]\pi^-[/math]	[math]\pi^-[/math]
B>0	B<0
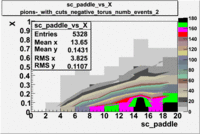
[math]\pi^+[/math]	[math]\pi^+[/math]
B>0	B<0

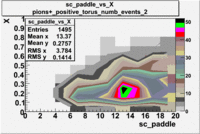
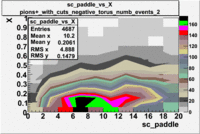
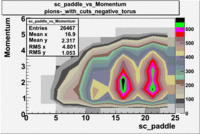
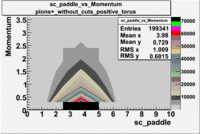
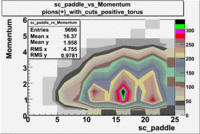
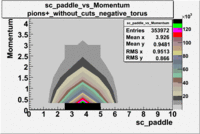
sc_paddle vs Momentum 5.7 GeV Beam Energy

There is a curvature problem.  When B > 0 then I expect the high momentum electrons to hit the lower
paddle numbers   (inbending).   I can see this when I look at the B>0 plot for electrons with cuts.  
When B < 0 then the electrons  are bending outwards which makes me expect the the higher momentum
electrons will high the higher numbered paddles.  I do not see this for B>0 with electron cuts.

no cuts	cuts	no cuts	cuts
Electons	B > 0		B<0
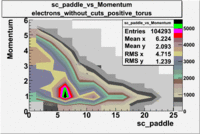
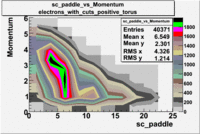
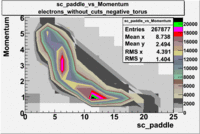
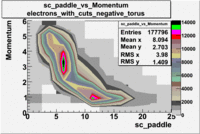
[math]\pi^-[/math]	B > 0		B<0
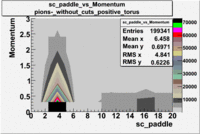
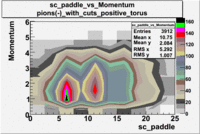
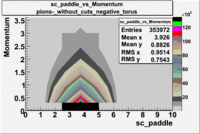
[math]\pi^+[/math]	B > 0		B<0

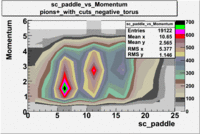
sc_paddle vs Momentum with cuts 5.7 GeV Beam Energy(number of events=2)

[math]\pi^-[/math]	[math]\pi^-[/math]
B>0	B<0
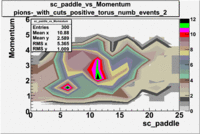
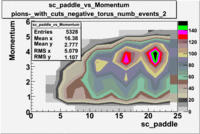
[math]\pi^+[/math]	[math]\pi^+[/math]
B>0	B<0

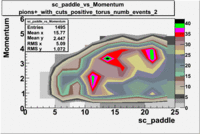
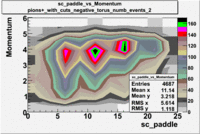
Used file dst26988_05.B00(Energy=5.7GeV and Torus=-2250)

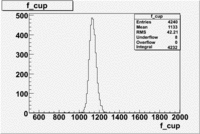
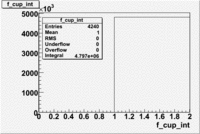
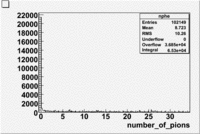
Paddle 7 Rates and statistics

The number of events per trigger is measured for the respective DST file above and then the Total number events in the data set is estimated from that.

[math]X_{bj}[/math]	[math]\pi^-[/math](B>0)		[math]\pi^+[/math](B<0)
	Total Number Events [math](10^{3})[/math]	Number events per [math]10^6[/math] triggers	Total Number Events [math](10^{3})[/math]	Number events per [math]10^6[/math] trigger
0.1	5.1	71	24.6	547
0.2	6.9	96	13.7	305
0.3	3.7	51	6.2	137
0.4	3.3	45	2.7	60
0.5	0.9	13	0.99	22

Paddle 17 Rates and statistics

[math]X_{bj}[/math]	[math]\pi^-[/math](B<0)		[math]\pi^+[/math](B>0)
	Total Number Events [math](10^{3})[/math]	Number events per [math]10^{6}[/math] trigger	Total Number Events [math](10^{3})[/math]	Number events per [math]10^{6}[/math] trigger
0.1	6.2	137	4.6	64
0.2	3.5	79	4.9	67
0.3	1.7	39	2.6	36
0.4	0.3	7	2.1	29
0.5	0.1	2	0.6	8

Paddle 5 and 8 Rates and statistics for electrons

[math]X_{bj}[/math]	[math]e^-[/math] sc_paddle=5 (B>0)		[math]e^-[/math] sc_paddle=8 (B<0)
	Total Number Events [math](10^{3})[/math]	Number events per [math]10^{6}[/math] trigger [math](10^{3})[/math]	Total Number Events [math](10^{3})[/math]	Number events per [math]10^{6}[/math] trigger [math](10^{4})[/math]
0.1	384.9	5.314	1665.2	3.706
0.2	382.5	5.282	977.8	2.176
0.3	264.9	3.657	567.1	1.262
0.4	159.5	2.202	328.6	0.7313
0.5	99	1.367	218.2	0.4856

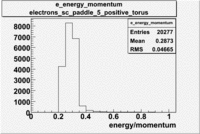
Histograms for 5.7 GeV Beam Energy

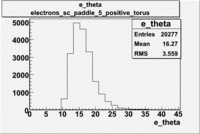
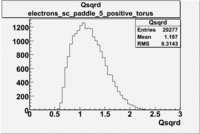
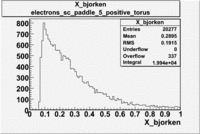
Electron energy/momentum	Electron Theta ([math]\theta[/math])	Electron Qsqrd	Electron X_bjorken
B>0 and sc_paddle=5
B<0 and sc_paddle=8

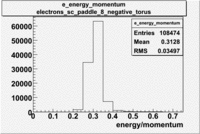
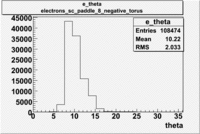
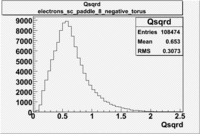
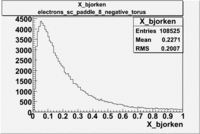
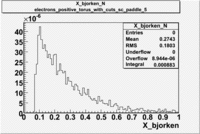
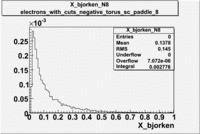
Normalized X_bjorken for electrons

B>0 and sc_paddle=5	B<0 and sc_paddle=8

Systematic Errors

Media:SebastianSysErrIncl.pdf Sebastian's Writeup