Forest NucPhys I

Advanced Nuclear Physics

References:

Introductory Nuclear Physics

Kenneth S. Krane: ISBN 9780471805533

Catalog Description:

PHYS 609 Advanced Nuclear Physics 3 credits. Nucleon-nucleon interaction, bulk nuclear structure, microscopic models of nuclear structure, collective models of nuclear structure, nuclear decays and reactions, electromagnetic interactions, weak interactions, strong interactions, nucleon structure, nuclear applications, current topics in nuclear physics. PREREQ: PHYS 624 OR PERMISSION OF INSTRUCTOR.

PHYS 624-625 Quantum Mechanics 3 credits. Schrodinger wave equation, stationary state solution; operators and matrices; perturbation theory, non-degenerate and degenerate cases; WKB approximation, non-harmonic oscillator, etc.; collision problems. Born approximation, method of partial waves. PHYS 624 is a PREREQ for 625. PREREQ: PHYS g561-g562, PHYS 621 OR PERMISSION OF INSTRUCTOR.

NucPhys_I_Syllabus

Click here for Syllabus

Introduction

The interaction of charged particles (electrons and positrons) through the exchange of photons is described by a fundamental theory known as Quantum ElectroDynamics(QED). QED has perturbative solutions which are limited in accuracy only by the order of the perturbation you have expanded to. As a result, the theory is quite useful in describing the interactions of electrons that are prevalent in Atomic physics.

Nuclear physics describes how Atomic nuclei interact via the strong forces as well as how the strong force binds the constituents of a nucleus (protons and neutrons, a.k.a. nucleons). Particle physics studies the interactions of fundamental particles, particles without substructure like quarks, photons, and electrons. Both Nuclear and Particle physics rely on the "Standard Model", a field theory description of the strong, weak and electromagnetic forces. Quantum ChromoDynamic (QCD) is one component to the Standard Model which represents the fundamental theory developed to describe the interactions of the quarks and gluons inside a nucleon, analogous to how QED describes the electromagnetic forces of electrons within the atom. The electroweak and Higgs field are the remaining components to the Standard model. Ideally, QCD is a field theory which could be used to describe how quarks interact to for nucleons and then describe how those nucleons interact to form a nucleus and eventually lead to a description of how the nucleus interacts with other nuclei. Unfortunately, QCD does not have a complete solution at this time. At very high energies, QCD can be solved perturbatively. This is an energy $E$ at which the strong coupling constant $\alpha_s$ is less than unity where

$\alpha_s \approx \frac{1}{\beta_o \ln{\frac{E^2}{\Lambda^2_{QCD}}}}$

$\Lambda_{QCD} \approx 200 MeV$

The objectives in this class will be to discuss the basic aspects of the nuclear phenomenological models used to describe the nucleus of an atom in the absence of a QCD solution.

Nomenclature

Variable	Definition
Z	Atomic Number = number of protons in an atom
A	Atomic Mass
N	number of neutrons in an atom = A-Z
Nuclide	A specific nuclear species
Isotope	Nuclides with same Z but different N
Isotones	Nuclides with same N but different Z
Isobars	Nuclides with same A
Nuclide	A specific nuclear species
Nucelons	Either a neutron or a proton
J	Nuclear Angular Momentum
$\ell$	angular momentum quantum number
s	instrinsic angular momentum (spin)
$\vec{j}$	total angular momentum = $\vec{\ell} + \vec{s}$
$Y_{\ell,m_{\ell}}$	Spherical Harmonics, $\ell$ = angular momentum quantum number, $m_{\ell}$ = projection of $\ell$ on the axis of quantization
$\hbar$	Planks constant/2$\pi = 6.626 \times 10^{-34} J \cdot s / 2 \pi$

Notation

${A \atop Z} X_N$ = An atom identified by the Chemical symbol $X$ with $Z$ protons and $N$ neutrons.

Notice that $Z$ and $N$ are redundant since $Z$ can be identified by the chemical symbol $X$ and $N$ can be determined from both $A$ and the chemical symbol $X$(N=A-Z).

example

${208 \atop\; }Pb ={208 \atop 82 }Pb_{126}$

Historical Review

Rutherford Nuclear Atom (1911)

Rutherford interpreted the experiments done by his graduate students Hans Geiger and Ernest Marsden involving scattering of alpha particles by the thin gold-leaf. By focusing on the rare occasion (1/20000) in which the alpha particle was scattered backward, Rutherford argued that most of the atom's mass was contained in a central core we now call the nucleus.

Chadwick discovers neutron (1932)

Prior to 1932, it was believed that a nucleus of Atomic mass $A$ was composed of $A$ protons and $(A-Z)$ electrons giving the nucleus a net positive charge $Z$. There were a few problems with this description of the nucleus

1. A very strong force would need to exist which allowed the electrons to overcome the coulomb force such that a bound state could be achieved.
2. Electrons spatially confined to the size of the nucleus ($\Delta x \sim 10^{-14}m = 10 \;\mbox{fermi})$ would have a momentum distribution of $\Delta p \sim \frac{\hbar}{\Delta x} = 20 \frac{\mbox {MeV}}{\mbox {c}}$. Electrons ejected from the nucleus by radioactive decay ($\beta$ decay) have energies on the order of 1 MeV and not 20.
3. Deuteron spin: The total instrinsic angular momentum (spin) of the Deuteron (A=2, Z=1) would be the result of combining two spin 1/2 protons with a spin 1/2 electron. This would predict that the Deuteron was a spin 3/2 or 1/2 nucleus in contradiction with the observed value of 1.

The discovery of the neutron as an electrically neutral particle with a mass 0.1% larger than the proton led to the concept that the nucleus of an atom of atomic mass $A$ was composed of $Z$ protons and $(A-Z)$ neutrons.

Powell discovers pion (1947)

Although Cecil Powell is given credit for the discovery of the pion, Cesar Lattes is perhaps more responsible for its discovery. Powell was the research group head at the time and the tradition of the Nobel committe was to award the prize to the group leader. Cesar Lattes asked Kodak to include more boron in their emulsion plates making them more sensitive to mesons. Lattes also worked with Eugene Gardner to calcualte the pions mass.

Lattes exposed the plates on Mount Chacaltaya in the Bolivian Andes, near the capital La Paz and found ten two-meson decay events in which the secondary particle came to rest in the emulsion. The constant range of around 600 microns of the secondary meson in all cases led Lattes, Occhialini and Powell, in their October 1947 paper in 'Nature ', to postulate a two-body decay of the primary meson, which they called p or pion, to a secondary meson, m or muon, and one neutral particle. Subsequent mass measurements on twenty events gave the pion and muon masses as 260 and 205 times that of the electron respectively, while the lifetime of the pion was estimated to be some 10-8 s. Present-day values are 273.31 and 206.76 electron masses respectively and 2.6 x 10-8 s. The number of mesons coming to rest in the emulsion and causing a disintegration was found to be approximately equal to the number of pions decaying to muons. It was, therefore, postulated that the latter represented the decay of positively-charged pions and the former the nuclear capture of negatively-charged pions. Clearly the pions were the particles postulated by Yukawa.

In the cosmic ray emulsions they saw a negative pion (cosmic ray) get captured by a nucleus and a positive pion (cosmic ray) decay. The two pion types had similar tracks because of their similar masses.

Nuclear Properties

NuclearProperties_Forest_NucPhys_I

The nucleus of an atom has such properties as spin, mangetic dipole and electric quadrupole moments. Nuclides also have stable and unstable states. Unstable nuclides are characterized by their decay mode and half lives.

Decay Modes

Mode	Description
Alpha decay	An alpha particle (A=4, Z=2) emitted from nucleus
Proton emission	A proton ejected from nucleus
Neutron emission	A neutron ejected from nucleus
Double proton emission	Two protons ejected from nucleus simultaneously
Spontaneous fission	Nucleus disintegrates into two or more smaller nuclei and other particles
Cluster decay	Nucleus emits a specific type of smaller nucleus (A1, Z1) smaller than, or larger than, an alpha particle
Beta-Negative decay	A nucleus emits an electron and an antineutrino
Positron emission(a.k.a. Beta-Positive decay)	A nucleus emits a positron and a neutrino
Electron capture	A nucleus captures an orbiting electron and emits a neutrino - The daughter nucleus is left in an excited and unstable state
Double beta decay	A nucleus emits two electrons and two antineutrinos
Double electron capture	A nucleus absorbs two orbital electrons and emits two neutrinos - The daughter nucleus is left in an excited and unstable state
Electron capture with positron emission	A nucleus absorbs one orbital electron, emits one positron and two neutrinos
Double positron emission	A nucleus emits two positrons and two neutrinos
Gamma decay	Excited nucleus releases a high-energy photon (gamma ray)
Internal conversion	Excited nucleus transfers energy to an orbital electron and it is ejected from the atom

Time

Time scales for nuclear related processes range from years to $10^{-20}$ seconds. In the case of radioactive decay the excited nucleus can take many years ($10^6$) to decay (Half Life). Nuclear transitions which result in the emission of a gamma ray can take anywhere from $10^{-9}$ to $10^{-12}$ seconds.

Units and Dimensions

Variable	Definition
1 fermi	$10^{-15}$ m
1 MeV	=$10^6$ eV = $1.602 \times 10^{-13}$ J
1 a.m.u.	Atomic Mass Unit = 931.502 MeV

Resources

The following are resources available on the internet which may be useful for this class.

Lund Nuclear Data Service

in particular

The Lund Nuclear Data Search Engine

Several Table of Nuclides

BNL
LANL
Korean Atomic Energy Research Institute
National Physical Lab (UK)

Table of Isotopes at Lawrence Berkeley National Laboratory

Quantum Mechanics Review

Quantum_Mechanics_Review_Forest_NucPhys_I

Nuclear Properties

NuclearProperties_Forest_NucPhys_I

The Nuclear Force

Deriving the Coulomb Force

TF_DerivationOfCoulombForce

Poisson's Equation

$\del^2 \phi(\vec{\eta}) = - \frac{e}{\epsilon_0} \delta(\vec{\eta})$

Nucleon- Nucleon scattering

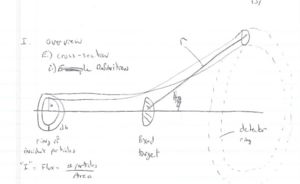
Cross section

Total cross section

$\sigma$ = $\equiv \frac{\# particles\; scattered} {\frac{ \# incident \; particles}{Area}} = \frac{j_{scattered} A}{j_{incident}}$

$j =$ current density = # scattered particles per Area.

Particles are scattered in all directions. Typically you measure the number of scattered particle with a detector of fixed surface area that is located a fixed distance away from the scattering point thereby subtending a solid angle as shown below.

Solid Angle

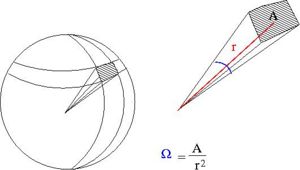
$\Omega$= surface area of a sphere covered by the detector

ie;the detectors area projected onto the surface of a sphere

A= surface area of detector

r=distance from interaction point to detector

$\Omega = \frac{A}{r^2}$sterradians

$A_{sphere} = 4 \pi r^2$ if your detector was a hollow ball

$\Omega_{max} = \frac{4 \pi r^2}{r^2} = 4\pi$sterradians

Differential cross section

$\sigma(\theta)$ = $\frac{d \sigma}{d \Omega} \equiv \frac{\frac{\# particles\; scattered}{solid \; angle}} {\frac{ \# incident \; particles}{Area}}$

Units

Cross-sections have the units of Area

1 barn = $10^{-28} m^2$

[units of $\sigma(\theta)$] =$\frac{\frac{[particles]}{[sterradian]}} {\frac{ [ particles]}{[m^2]}} = m^2$

Fixed target scattering

$N_{in}$= # of particles in = $I \cdot A_{in}$

$A_{in}$ is the area of the ring of incident particles

$dN_{in} = I \cdot dA = I (2\pi b) db$= # particles in a ring of radius $b$ and thickness $db$

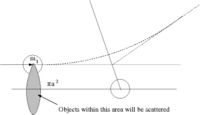
Scattering Length (a)

Definition

$a^2 = \frac{1}{4 \pi} \lim_{k \rightarrow 0} \sigma$

While scattering length has the dimension of length it really represents the strength of the scattering (probability of scattering). It effectively give the amplitude of the scattered wave.

Note

the above definition is essentially an expression of how the low energy cross section corresponds to the classical value of $4 \pi a^2$

$\sigma$ = scattering cross-section $\equiv \frac{\# particles\; scattered} {\frac{ \# incident \; particles}{Area}}$

classically: the number of particles scattered = number of incident particles (the collision probability is unity)

Area = $\pi a^2$ = The area profile in which a collision occurs

$\sigma = \frac{{N}}{\frac{ N}{\pi a^2}} = \pi a^2$

To derive an expression for the scattering length lets start with a general expression for a scattered wave.

A general scattered wave function has the form

$\Psi_g = \frac{1}{(2 \pi)^{3/2}} \left [ e^{i \vec{k} \cdot \vec{r}} + f(q) \frac{e^{ikr}}{r}\right ]$

The first term represents a plane wave and the second term represent a modification of the plane wave due to the scattering in terms of the scattering probability $|f(q)|^2$.

From our previous phase shift calculation, Schrodinger solutions tend to have the general form

$\Psi_S = \sum_{\ell} A_{\ell} P_{\ell} [\cos(\theta)] \frac{U_{\ell}(r)}{kr}$

$= \sum_{\ell} A_{\ell} P_{\ell} [\cos(\theta)] \frac{\sin(kr - \frac{\ell \pi}{2} + \delta_{\ell})}{kr}$ (our previous solution was for $\ell=0$)

where

the angular part is given as

$P_{\ell} \cos(\theta)$

and the radial part is

$\frac{U_{\ell}(r)}{r}$

By comparing our general solution from the phase shift and our schrodinger solution we can cast f(q) in terms of the phase shift $\delta_{\ell}$ and then define the cross section as

$\sigma = \int |f(q)|^2 d \Omega$

in order to get a gereral expression for a scattering cross section which we then take the limit of the momentum going to zero in order to get a general expression for the scattering length.

Math trick to recast plane waves

$e^{i\vec{k} \cdot \vec{r}} = 4 \pi \sum_{\ell m} i^{\ell} Y^*_{\ell m}(\hat{k}) Y_{\ell m}(\hat{r}) J_{\ell m}(|k| |r|)$

where

$\hat{k}$ and $\hat{r}$ are the $\theta$ and $\phi$ directions of $\vec{k}$ and $\vec{r}$ respectively.

To determine the scattering length we will be looking at $k \rightarrow 0$ so let $\hat{k}=0 \Rightarrow \theta=0 , \phi=0$ use the approximation

$Y^*_{\ell m}(\theta=0,\phi=0) = \sqrt{\frac{2 \ell +1}{4 \pi}}\delta_{m,0}$

using the above to recast $\Psi_g$ to look more like $\Psi_S$

$\Psi_g = \frac{1}{(2 \pi)^{3/2}} \left \{ 4 \pi \sum_{\ell} i^{\ell} \sqrt{\frac{2 \ell +1}{4 \pi}}\delta_{m,0} Y_{\ell m}(\hat{r}) J_{\ell m}(|k| |r|) + f(q) \frac{e^{ikr}}{r} \right \}$

$\delta_{m,0} Y_{\ell m}(\hat{r}) =Y_{\ell 0}(\hat{r}) = \sqrt{\frac{2 \ell +1}{4 \pi}} P_{\ell} [\cos(\theta)]$

$\Rightarrow \Psi_g = \frac{1}{(2 \pi)^{3/2}} \left \{ \sum_{\ell} i^{\ell} (2 \ell +1) P_{\ell} [\cos(\theta)] J_{\ell m}(|k| |r|) + f(q) \frac{e^{ikr}}{r} \right \}$

which we want to compare to \Psi_S

$\Psi_S = \sum_{\ell} A_{\ell} P_{\ell} [\cos(\theta)] \frac{\sin(kr - \frac{\ell \pi}{2} + \delta_{\ell})}{r}$

Using the identities:

$\sin(kr - \frac{\ell \pi}{2} + \delta_{\ell}) = \frac{e^{i(kr - \frac{\ell \pi}{2} + \delta_{\ell})} - e^{-i(kr - \frac{\ell \pi}{2} + \delta_{\ell})}}{2i}$

$J_{\ell m}(|k| |r|) = \frac{e^{i(kr - \frac{\ell \pi}{2} )} - e^{-i(kr - \frac{\ell \pi}{2} )}}{2ir}$

By equating the two solutions

$\Psi_S = \Psi_g$

$e^{-ikr} \Rightarrow A_{\ell} e^{i\delta_{\ell}} = \frac{i^{\ell} (2 \ell +1)}{(2 \pi)^{3/2}}$

$e^{+ikr} \Rightarrow$

$\sum_{\ell} \frac{A_{\ell}}{kr} P_{\ell} [\cos(\theta)]e^{i (kr - \frac{\ell \pi}{2} + \delta_{\ell})} = \sum_{\ell} \frac{i^{\ell} (2 \ell +1)}{(2 \pi)^{3/2} 2ikr} P_{\ell} [\cos(\theta)]e^{i(kr - \frac{\ell \pi}{2} )} + \frac{f(q) e^{ikr}}{(2 \pi)^{3/2}r}$

$\Rightarrow \frac{f(q) e^{ikr}}{(2 \pi)^{3/2}r}= \sum_{\ell} \frac{ P_{\ell} [\cos(\theta)]}{2ikr} e^{- i \ell \pi/2} \left ( \frac{A_{\ell}}{kr} e^{i (kr - \frac{\ell \pi}{2} + \delta_{\ell})} - \frac{i^{\ell} (2 \ell +1)}{(2 \pi)^{3/2}} e^{i(kr - \frac{\ell \pi}{2} )} \right )$

$= \sum_{\ell} \frac{A_{\ell}}{kr} e^{i (kr - \frac{\ell \pi}{2} + \delta_{\ell})} - \frac{i^{\ell} (2 \ell +1)}{(2 \pi)^{3/2} 2ikr} P_{\ell} [\cos(\theta)]e^{i(kr - \frac{\ell \pi}{2} )}$

$\Rightarrow f(q) = \frac{1}{k} \sum_{\ell} (2 \ell + 1 ) P_{\ell} [\cos(\theta)] \sin(\delta_{\ell}) e^{i \delta_{\ell}}$

$\sigma = \int | f(q) |^2 d \Omega$

$= \sum_{\ell \ell^{\prime}} \int \frac{2 \ell + 1 )(2 \ell^{\prime} + 1)}{k^2}P_{\ell} [\cos(\theta)] \sin(\delta_{\ell}) e^{i \delta_{\ell}} P_{\ell^{\prime}} [\cos(\theta)] \sin(\delta_{\ell^{\prime}}) e^{-i \delta_{\ell^{\prime}}}$

$\int P_{\ell} P_{\ell^{\prime}} d \theta = \frac{2}{2 \ell + 1} \delta_{\ell \ell^{\prime}}$

$\Rightarrow \sigma = \frac{4 \pi}{k^2} \sum_{\ell} (2 \ell +1 ) \sin^2(\delta_{\ell})$

$a^2 = \frac{1}{4 \pi} \lim_{k \rightarrow 0} \sigma = \frac{1}{4 \pi} \lim_{k \rightarrow 0} \frac{4 \pi}{k^2} \sum_{\ell} (2 \ell +1 ) \sin^2(\delta_{\ell})$

For S-wave scattering $\ell =0$

$\Rightarrow a = \pm \lim_{k \rightarrow 0} \frac{\sin(\delta_0)}{k}$

To keep "a" finite the phase shift $\delta_{\ell}$ must approach zero at low energy

$\Rightarrow a = \pm \lim_{k \rightarrow 0} \frac{\delta_0}{k}$

Singlet and Triplet States

Our previous calculation of the total cross section for nucleon nucleon scattering using a phase shift analysis gave

$\sigma = \frac{4 \pi}{k_2^2}\sin^2(\delta_0)$

assuming $\ell$ =0.

When solving Schrodinger's equation for a neutron scattering from a proton we were left with the transcendental equation from boundary conditions

$\alpha \equiv k_1 cot(k_1R) = k_2 cot(k_2R + \delta)$

$\sigma = \frac{4 \pi}{ k_2^2 + \alpha^2} \left [\cos(k_2 R) + \frac{\alpha}{k_2} \sin(k_2R)\right ]$

In the case of a Deuteron bound state

$\ell =0$ and $S=1$

R = 2 fm

$\alpha$ = 0.2 /fm

when $k_2 \rightarrow 0$

$\frac{\sin(k_2 R)}{k_2} = R$

$\cos(k_2 R) = 1$

then

$\lim_{k_2 \rightarrow 0} \sigma = \frac{4 \pi}{ 0 + (0.2)^2} \left [1 + (0.2) 2\right ] \left ( \frac{1 barn}{100 fm^2}\right)= 4.4 barns$

Experimentally the cross section is quite a bit larger

$\sigma_{Exp}$ = 20.3 b

Apparently our assumption that the dominant part of the cross section is S=1 is wrong. There also exists a spin singlet (S=0) contribution to the cross section.

When the neutron and proton interact (create a bound state or an intermediate state) their spins can couple to either a net value of S=0 or S=1. There is only one component along the quantization axis in the event that they couple to an S=0 state. There are 3 possible components ($S_z$ = -1/2, 0 . + 1/2) in the event that they couple to an S=1 state.

If you sum up the two possible cross-section,$\sigma_S$ and $\sigma_T$, then you must weight them according to the possible psin compinations such that

$\sigma_{tot} = \frac{3}{4} \sigma_T + \frac{1}{4} \sigma_S$

Solving for $\sigma_S \Rightarrow$

$\sigma_S = 68$ barns

Because the cross sections depend on the spin date we can conclude that

The Nuclear Force is SPIN DEPENDENT

Also

Using the spatial wave functions for the singlet and triplet state one can deduce that

$a_T$ = + 6.1 fm $\Rightarrow$ there is a triplet np bound state

$a_S$ = - 23.2 fm $\Rightarrow$ there is NO singlet np bound state

Doing similar but more complicated calculations for p-p and n-n scattering results in

$a_{p-p}$ = -7.82 fm $\Rightarrow$ there is NO pp bound state

$a_{n-n}$ = -16.6 fm $\Rightarrow$ there is NO nn bound state

The Nuclear Potential

From the above we have found information on the range of the nuclear force, it's spin dependence, and it's ability to create non-spherically disrtibuted systems (quadrupole moments).

The Central Potential

No matter what potential Well geometry we choose for the nucleon, we consistently find a term which is purely radial in nature (a Central term).

$\lt V_c(r)\gt = \int U^*(r) V_c(r) U(r) dr = \frac{\hbar (\ell + 1) \ell}{2m} \int |U(r)|^2G(\delta) \frac{dr}{r^2}$

where

$G(\delta)$ = a parameterization of$V_c$ which is constrained by scattering phase shift information.

The Spin Potential

We know from the lack of a p-p $(^2NHe)$ or n-n bound system that the nuclear force is strongly spin dependent. This is reenforced even more based on our observations of the S=1 n-p bound state (the Deuteron).

Experiments also indicate that parity is conserved to the $10^{-7}$ level. $\Rightarrow$ experiments with an relative precision of $\frac{\Delta X}{X} \gt 10^{-7}$ have yet to find a parity violation.

$\Rightarrow$ The spin potential would have terms involving spin scalar quantities because a spin potential with terms that are linear combinations of spin would violate parity.

Consider a spin potential function such that the total spin is given by

$\vec{S} = \vec{s}_1 + \vec{2}_2$

The scalar spin quantity $S^2$ would be given by

$\vec{S} \cdot \vec{S} = s_1^2 + 2\vec{s}_1 \cdot \vec{s}_2 + s_2^2$

or

$\vec{s}_1 \cdot \vec{s}_2 = S^2 -s_1^2-s_2^2$

Spin Singlet

if

S=0

then

$\lt \vec{s}_1 \cdot \vec{s}_2 \gt = \lt S^2\gt -\lt s_1^2\gt -\lt s_2^2\gt$

$= \left [ S(S+1) - s_1(s_1+1) - s_2(s_2+1) \right ] \frac{\hbar^2}{2}$

$= \left [ 0(0+1) - \frac{1}{2} (\frac{1}{2}+1)- \frac{1}{2} (\frac{1}{2}+1)\right ] \frac{\hbar^2}{2}$

$= - \frac{3}{4} \hbar^2$

Spin Triplet

if

S=1

then

$\lt \vec{s}_1 \cdot \vec{s}_2 \gt = \lt S^2\gt -\lt s_1^2\gt -\lt s_2^2\gt$

$= \left [ S(S+1) - s_1(s_1+1) - s_2(s_2+1) \right ] \frac{\hbar^2}{2}$

$= \left [ 1(1+1) - \frac{1}{2} (\frac{1}{2}+1)- \frac{1}{2} (\frac{1}{2}+1)\right ] \frac{\hbar^2}{2}$

$= + \frac{1}{4} \hbar^2$

Construct the Spin Potential

Let

V_1(r) = spin singlet parameterized potential

V_3(r) = spin triplet parameterized potential

Then

V_s(r) = - (

Nuclear Models

Given the basic elements of the nuclear potential from the last chapter, one may be tempted to construct the hamiltonian for a group of interacting nucleons in the form

$H = \sum_i^A T_i + \sum_i\lt j^A V_{ij}$

where

$T_i$ represent the kinetic energy of the ith nucleon

$V_{ij}$ represents the potential energy between two nucleons.

If you assume that the nuclear force is a two body force such that the force between any two nucleons doesn't change with the addition of more nucleons, Then you can solve the Schrodinger equation corresponding to the above Hamiltonian for A<5.

For A< 8 there is a technique called Green's function monte carlo which reportedly finds solution that are nearly exact. J. Carlson, Phys. Rev. C 36, 2026 - 2033 (1987), B. Pudliner, et. al., Phys. Rev. Lett. 74, 4396 - 4399 (1995)

Shell Model

Independent particle model

This part of the Shell model suggests that the properties of a nucleus with only one unpaired nucleon are determined by that one unpaired nucleon. The unpaired nucleon usually, though no necessarily, occupies the outer most shell as a valence nucleon.

SN-130 Example

The low lying excited energy states for Sn-130 taken from the LBL website are given below.

File:Sn-130 LowLyingE Levels.tiff

The listing indicates that the ground state of Sn-130 is a spin 0 positive parity $(J^{\pi} = 0^+)$ state. The first excited state of this nucleus is 1.22 MeV above the ground state and has $(J^{\pi} = 2^+)$. The next excited state is 1.95 MeV above the ground state and has $(J^{\pi} = 7^-)$.

Let's see how well the shell model does at predicting these $(J^{\pi} )$ states

Liquid Drop Model

Bohr and Mottelson considered the nucleon in terms of its collective motion with vibrations and rotations that resembled a suspended drop of liquid.

Electric Quadrupole Moment

Electric_QuadrupoleMoment_Forest_NuclPhys_I

Nuclear Decay

Nuclear_Decay_Forest_NucPhys_I

Nuclear Reactions

Forest_NucPhys_I_Nuclear_Reactions

Homework problems

NucPhys_I_HomeworkProblems

Midterm Exam Topics list

Basically everything before section 5.3 (The Nuclear Force). Section 5.3 and below is not included on the midterm.

Topics of emphasis:

1. 1-D Schrodinger Equation based problems involving discrete potentials ( wells, steps) and continuous potentials (simple Harmonic, coulomb).
2. Calculating form factors given the density of a nucleus
3. Determining binding and nucleon mass separation energies
4. $\vec{I}$, $\vec{\ell}$, and $\vec{s}$ angular momentum operations
5. Calculating scattering rates given the cross-section and a description of the experimental apparatus

Formulas given on test

Schrodinger Time independent 1-D equation

$\left ( \frac{- \hbar^2}{2m} \frac{ \part^2}{\part x^2} + V \right ) \psi = E \psi$

Particle Current Density

$j = \frac{ \hbar}{2im} \left ( \Psi^* \frac{\part \Psi}{\part x} - \Psi \frac{\part \Psi^*}{\part x}\right )$

Form Factor

If the density has no $\theta$ or $\phi$ dependence

$F(q) = \frac{4 \pi}{q} \int \sin(qr) \rho(r) rdr$

Coulomb energy difference between point nucleus and one with uniform charge distribution

$\Delta E = \frac{2}{5} \frac{Z^4e^2}{4 \pi \epsilon_0} \frac{R^2}{a_0^3}$

Nucleus Binding Energy

$B(^A_ZX_N) = \left [ Z m(^1H) + Nm_n -m(^AX) \right ]c^2$

Neutron Separation energy

$S_n = B(^A_ZX_N) - B(^{A-1}_ZX_{N-1})$

Proton Separation energy

$S_p = B(^A_ZX_N) - B(^{A-1}_{Z-1}X_N)$

Semiempirical Mass Formula

$M(Z,A) = Z m(^1H) + Nm_n - B(^A_ZX_N)/c^2$

where

$B(^A_ZX_N) = = \alpha_V A - \alpha_S A^{2/3} - \alpha_C \frac{Z(Z-1)}{A^{1/3}} - \alpha_{sym} \frac{(A-2Z)^2}{A} - \delta$

Parameter	Krane
$\alpha_V$	15.5
$\alpha_S$	16.8
$\alpha_C$	0.72
$\alpha_{sym}$	23
$\alpha_p$	$\pm$34

$g_{\ell} =\left \{ {1 \;\;\;\; proton \atop 0 \;\;\;\; neutron} \right .$

$g_{s} =\left \{ {5.5856912 \pm 0.0000022 \;\;\;\; proton \atop -3.8260837 \pm 0.0000018 \;\;\;\; neutron} \right .$

Final

1.) Calculate the magnetic moment of a proton assuming that it may be described as a neutron with a positive pion $(\pi^+)$ in an $\ell =1$ state.

2.) Show that the phase shift ($\delta_0$) for the scattering of a neutron by a proton can be given by the equation

$\delta_0 = \tan^{-1} \left( \frac{\tan(k_1R) - \frac{k_1}{k_2} \tan(k_2R)}{ \tan(k_1R) \tan(k_2R)+\frac{k_1}{k_2}}\right )$

where

$k_1^2 = \frac{2m(V+E)}{\hbar^2}$

$k_2^2 = \frac{2mE)}{\hbar^2}$

V = 36.7 MeV R = 2.1 fm

3.)

a.) Write the reaction equations for the following processes. Show all reaction products.

i.)${226 \atop\; }Ra \; \; \; \alpha - decays$

ii.)${110 \atop\; }In \; \; \; \beta^+ - decays$

iii.)${36 \atop\; }Ar (2^{nd} 0^{+}) \; \; \; internal conversion$

iv.)${12 \atop\; }C (2^+) \; \; \; \gamma - decays$

b.) Determine the Q-values for the first two reactions above.

4.) Find the Quadrupole moment of ${209 \atop\; }Bi(9/2^-)$ using the shell model and compare to the experimental value of -0.37 barns.

5.) Find $\frac{\mu}{\mu_{NM}}$, using the shell model, for the following nuclei

a.)${75 \atop\; }Ge$

b.) ${87 \atop\; }Sr$

c.) ${91 \atop\; }Zr$

d.) ${47 \atop\; }Sc$

6.) Use the shell model to predict the ground state spin and parity of the following nuclei:

a.) ${7 \atop\; }Li$

b.)${11 \atop\; }B$

c.) ${15 \atop\; }C$

d.)${17 \atop\; }F$

7.) Tabulate the possible $m$ states for a nucleus three quadrupole phonon state ($\lambda = 3$ ). Show that the permitted resultant states are $0^+$, $2^+$, $3^+$, $4^+$, and $6^+$.