NuclearProperties Forest NucPhys I
Nuclear Properties
Quantum Chromodynamics (QCD) is the fundamental quantum field theory within the standard model that is used to describe the Strong interaction of the fundamental particles known as quarks and gluons, the constituents of a nucleon, in terms of their color. While the Strong force acts directly on the elementary quark and gluon particles, a residual of the force is observed acting between nucleons within an atomic nucleus that is referred to as the nuclear force. The degrees of freedom needed to describe the elementary particles within an average Atomic nucleus with A=50 makes a solution difficult. As a result, a phenomenological approach is used (i.e.: models) to describe nuclear physics processes. Below are some of the static properties of a nucleus that a quantum field theory or model would need to predict.
- nuclear charge and radius
- mass and binding energy
- angular momentum and parity
- magnetic dipole and electric quadrupole moments
- excited energy levels
These properties are explored further in the sections below.
Nuclear Charge and Radius
Once you know the Isotope then you know how many protons are in the nucleus of interest and therefore the charge.
The interest however is in how that charge is distributed inside the nucleus.
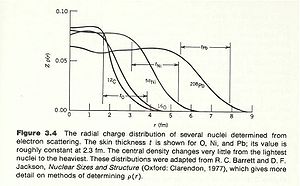
The density of nucleons within the nucleus tends to be uniform over a short distance and then rapidly goes to zero. There are two quantities which are used to characterize nuclear size.
- mean radius: The radius of the nucleus in which its density is half of its central value
- skin thickness: the distance over which the density of the nucleus drops from its max to its min.
Because the nucleus is charged one could also quantify the nuclear shape in term of
- electromagnetic multipole moments: charge = 1st moment, mag dipole = 2nd moment, electric quadrupole= 3rd moment
probe
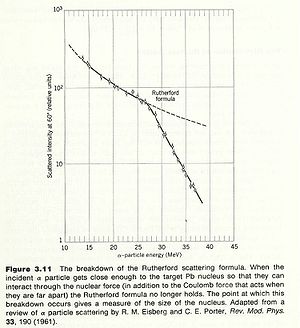
One of the first ways to measure the nuclear radius was to look for the failure of Rutherford scattering. Since Rutherford scattering only considers the coulomb repulsion of two charged object, one could assert that the physics changes when measurements of the scattered particles fail to obey the Rutherford prediction.
An alpha particle scattered from a Gold nucleus deviates from Rutherford scattering at incident alpha particle energies of about 27 MeV. If you assume that this is the energy at which the incident alpha particle starts to probe the inside of the nucleus then you can estimate the size of a uniformly charged spherical nucleus with a hard boundary as:
The modern value for the gold nucleus is 7.2 fm.
optical measure of radius
Quantum measure of radius:
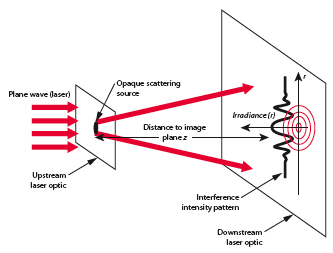
One direct method used to determine the size of an object in to alter the size of a probe until interference patterns emerge (ie ).
- Note
- The pattern broadens as .
By virtue particle wave duality, the elastic scattering of an electron from a nucleus can behave in a similar fashion to the scattering of light by an opaque target.
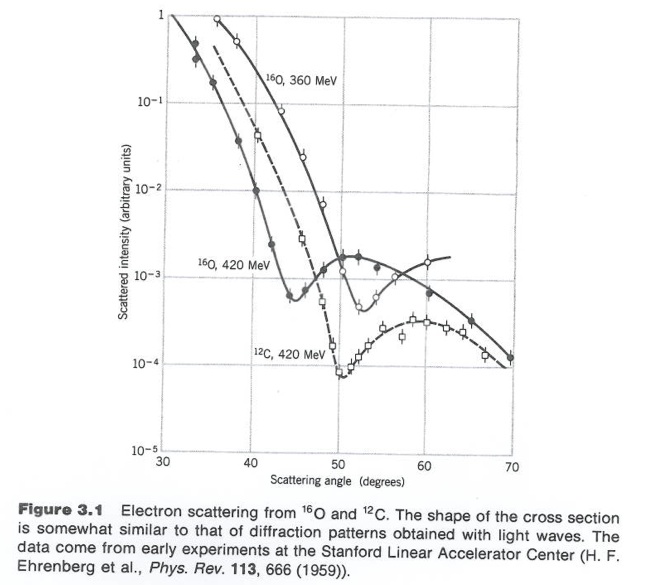
Figure 3.1 from Krane's book.
Although 3-D objects reveal diffraction patterns that are similar to those from a two dimensional disk, such comparisons are really only rough estimates. As we saw from the above, the scattering of photons from O-16 revealed a diffraction pattern. A similar diffraction pattern can be seen if you elastically scatter electrons from a Pb-208 nucleus.
Distribution of Nuclear Charge
For our current interest we would like a means to measure the distribution of charge in the nucleus of an atom. This can be accomplished by elastically scattering a probe off of the nucleus which is sensitive to charge. Elastically scattering an electron off of a nucleus is one such probe. A description of this can be found using Fermi's Golden Rule where the transition amplitude
is the main term in Fermi's Golden Rule which describes the interaction that takes place.
In our current example we have an incident electron plane wave in some initial state which gets elastically scattered by some charge distribution (a nucleus) to a final plane wave state by means of a coulomb interaction.
where
- integral over the volume of the nucleus
- integral over all space
- charge density as a function of R from the center of the nucleus
- distance of probe from the center of the nucleus
- momentum transfered to the charge distribution.
Let
Then
- Some integral
- Physics of interest = Fourier transform of
The inverse Fourier Transform would be
To find the charge density you would measure the transition rate as a function of the momentum transfer. The charge density will then be the inverse Fourier transform of that data.
The data below are the result of such measurements.
F(q) general form
Let
Charge Radius
A measure of can also be used to extract the charge radius
- : Density is normalized
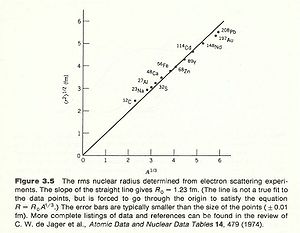
Take the derivative of F(q) with respect to Q then you get a slope of the function. The slope of this function near the origin(q=0) tells you the mean charge radius squared. Making these electron scattering measurements on several different nuclei has revealed a cubed root relationship between the radius and the atomic number A.
K X-ray isotope shift
Another method employed to measure the charge radius of a nucleus involves a measurement of the K X-rays produced by 2 different isotopes of the same atom.
A "K X-ray" is the photon given off when and electron undergoes a transition from the 2P orbit to the 1S.
Let
- = K X-ray energy from isotope (ie: A=208, Z=82, Pb-208)
- = K X-ray from isotope A^{\prime} (ie: = 207, Z=82 , Pb-207)
Assume
This assumes that the energy difference is a lot bigger than the difference for the 2P electrons. Since the energy difference we are investigating is caused by the 1S electron spending some time inside the nucleus sampling the nucleus' charge distribution, one can assert that the higher energy 2P electrons state spends substantially less time sampling the nuclear charge distribution.
Let
where
- energy level for an electron with a point nucleus
similarly
- change in the electron energy eigen value when the point like assumption for the nucleus is removed
Electron energy correction
Use the coulomb potential to calculate the change in the electron energy eigen value when the nucleus is given a finite instead of being point like.
An electron which has a finite probability of existing within a finite size nucleus, of radius , will feel a different coulomb potential when it is inside than outside. This possibility of having an electron spend some time inside the nucleus effectively changes its energy eigenvalue by an amount . This change in energy is
When the electron is outside the nucleus
substitution:
To make the calculation easy lets assume that the electrons wave function for a finite size nucleus is the same as the wave function for the point like nucleus. The radial wave function for Hydrogen is
- Bohr radius
Because the operator has no angular dependence we only need to do the radial part of the integral. The angular part of the integral is normalized to unity. So
Since
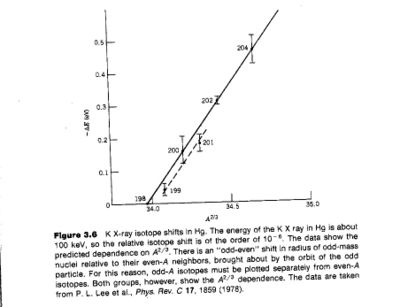
The K X-ray isotope shift is:
From electron scattering experiments we found that
If you measure the isotope shift you can infer
- Notice
- The slope of the fit shown (solid line for even nuclei) is about 10% higher than what is predicted
Using wave functions which account for relativistic effect moves the prediction into agreement with experiment.
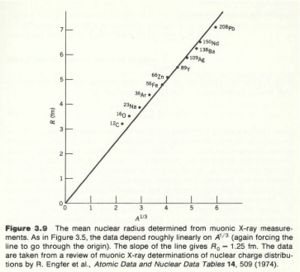
The experiment has been improved by using muonic atoms. A muonic atom has a muon in place of the electron. Because of its higher mass the muon has a tighter "orbit" , the muon isn't really orbiting the nucleus, and has a higher probability of being inside the nucleus thereby being more sensitive to the charge distribution. The X-rays emmited by muons cascading down the energy levels are in the MeV range while electrons are in the keV range.
Muon experiments have measured .
Coulomb Energy
Yet another method to determine the radius of a nucleus considers the impact of the coulomb force on the binding energy of Mirror nuclei. Mirror nuclei are two nuclei with the same number of nucleons but different number of protons and neutrons such that the number of protons (Z) in one nucleus is equal to the number of neutrons(N) in the other nucleus. For example He-3 (Z=2,N=1) and H-3 (Z=1, N=2). The difference in the coulomb binding energy of such mirror nuclei can be used to determine the radius of the nuclei.
If we assume the nucleus is a uniformly charge non-conducting sphere, then the "self energy", or the energy needed to assemble the charge distribution can be found using the work energy theorem for conservative forces.
- Work -Energy Theorem :work needed to assemble a charge distribution which corresponds to a potential energy U = qV
The potential energy for the assembled charge distribution would be
If you compare the coulomb energy difference between two mirror nuclei with one having Z protons and one have (Z-1) protons then the coulomb energy difference would be
For mirror nuclei : Z = N-1
- of the mirror nucleus
and
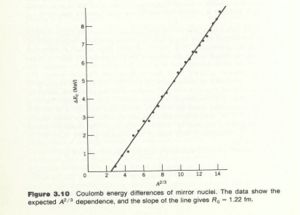
One way to measure is to detect the decay of a mirror nucleus in which the proton changes into a neutron and emits a positron. The Max positron energy observed is . If you plot as a function of then the slope is proportional to .
The graph below is from Krane's book
Matter radius
The above electron probe is a fine way to measure charge distribution in a nucleus. A nucleus however does contain uncharged nucleons known as neutrons. Neutrons do have a charge distribution, more positive core to a more negative surface charge. In order to measure the distribution of nuclear matter you will need to use a probe which depends more on the strong force and less on the electromagnetic.
Mesons (pions) are used in a manner similar to the use of muons by looking at the X-rays emmited as they cascade down the energy levels. A meson interacts with the nucleus through both the Strong and E&M forces.
Summary
There are 3 ways to characterize the nuclear shape
- mean radius:the density of nucleons within the nucleus drops to half its mean value
- skin thickness: The distance over which the density drops from a max to a min
- electromagnetic dipole moment: 1st moment = charge, 2nd moment = mag dipole, 3rd moment = electric quadrupole
Nuclear Binding Energy and Mass
Binding energy
The binding energy of a nucleus is defined as the mass difference between the constituents of a nucleus and the nucleus.
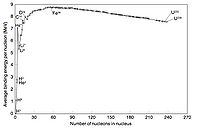
If you make a plot of B/A -vs- A for ground state nuclei you would see something similar to the curve below.
The above plots may be described by some closed functional form which
Volume Term
As seen in the above graph, the ratio of B/A is almost a constant 8 MeV until you start to get to low A (A<9). As we saw previously, the density of nucleon inside the nucleus appears to be constant until you get to the edge.
or in other words the atomic number is proportional to the volume of the nucleus. At first glance you can imaging the the nuclear force acting on a group of A nucleons would be proportional to thinking any given nucleon is experiencing a force from all the other nucleons. Based on the above graph you expect the binding energy to be proportional the the Atomic number, suggesting that the strong force is so short range that nucleons really only see their nearest neighbor.
So our first term to fit the above curve has the form
Surface Term
The next parameter for the fit function is called the surface term . Experiments have shown that as you get near the edge of a nucleus the density of nucleons changes. The nucleons on the surface of the nucleus have fewer nearest neighbors and they are farther apart (Less bound) from each other. As a result the surface term should reduce the overestimate from the volume term. Furthermore, if the volume term is proportional to A then the radius is proportional to so the surface (Area) term should be proportional to
Coulomb Term
While the nuclear force is trying to bind the nucleons, the coulomb force is trying to push protons apart thereby making them less bound. As we saw previously, the self energy of a uniformly charged sphere suggests that
which leads a reduction in the binding energy
Asymmetry Term
Stable isotopes tend to have Z ,
If Z is not half of A then you the nucleus is less bound (more unstable). So your expect a functional dependence like
to appear such that
- Note
- You may see the asymmetry term sometimes written as
Pairing Term
it is also observed that nucleons like to pair up ( spin couple) inside the nucleus. If you had an even number of nucleons you would be able to spin couple such that you can occupy a lower energy state. Whereas if you had an odd number of nucleons, you would have some less bound un-paired nucleons within the nucleus.
one functional form used for is
The sign of changes depending on if and are both even or both odd.
Semiemirical mass formula constants
| Parameter | Krane | Wapstra | Rohlf |
| 15.5 | 14.1 | 15.75 | |
| 16.8 | 13 | 17.8 | |
| 0.72 | 0.595 | 0.711 | |
| 23 | 19 | 23.7 | |
| 34 | 33.5 | 11.18 |
Except for the Rohlf measurements the "+" sign is used when N & Z are even and the "-" is used when N & Z are both odd integers.
Ref:
Wapstra: Atomic Masses of Nuclides, A. H. Wapstra, Springer, 1958
Rohlf: Modern Physics from a to Z0, James William Rohlf, Wiley, 1994
Semi-empirical (Weizacker) mass formula
The semi-empirical mass formula takes the definition of binding energy B(Z,A), solves for the mass of the nucleus, and then inserts the binding energy fit equation.
take the binding energy equation
and solve for the nucleus mass
Examples
BE(26,59)
Nucleon Separation Energies
Neutron Separation Energy== Energy needed to liberate a neutron from the Nucleus Proton Separation Energy== Energy needed to liberate a proton from the Nucleus
Mass decay chains
A=125 decay chain
| Isotope | B(MeV) | N | Z | t_{1/2} |
| Praseodymium (Pr-59) | 1020.67 | even | odd | 3.3 sec (inverse Beta) |
| Cerium (Ce-58) | 1030.1 | odd | even | 9 sec |
| Lanthanum (La-57) | 1038.21 | even | odd | 76 sec (inverse Beta) |
| Barium (Ba-56) | 1044.63 | odd | even | 3.5 min |
| Cesium (Cs-55) | 1049.98 | even | odd | 45 min (inverse Beta) |
| Xenon (Xe-54) | 1053.86 | odd | even | 16.9 hours |
| Iodine (I-53) | 1056.29 | even | odd | 59.41 days inverse beta decay |
| Tellurium (Te-52) | 1057.26 | odd | even | Stable |
| Antimony (Sb-51) | 1057.28 | even | odd | 2.76 years |
| Tin (Sn-50) | 1055.7 | odd | even | 9.64 days |
| Indium (In-49) | 1051.06 | even | odd | 12.2 sec |
| Cadmium (Cd-48) | 1044.72 | odd | even | 0.65 sec Beta decay |
A=128 decay chain
| Isotope | B(MeV) | N | Z | t_{1/2} |
| Lanthanum (La-57) | 1067.29 | odd | odd | 5 min |
| Barium (Ba-56) | 1074.73 | even | even | 2.43 days |
| Cesium (Cs-55) | 1076.03 | odd | odd | 3.66 min electron capture |
| Xenon (Xe-54) | 1080.74 | even | even | Stable |
| Iodine (I-53) | 1079.41 | odd | odd | 25 min Beta decay |
| Tellurium (Te-52) | 1081.44 | even | even | 10^24 years Stable for our lifetime |
| Antimony (Sb-51) | 1077.84 | odd | odd | 10.4 min |
| Tin (Sn-50) | 1077.35 | even | even | 59.07 min |
| Indium (In-49) | 1069.15 | odd | odd | 0.72,0.84 sec |
| Cadmium (Cd-48) | 1062.87 | even | even | 0.34 sec |
Angular Momentum and Parity
Angular Momentum (j)
Consider the case of a proton orbiting around a nuclear shell
- = orbital angular momentum
- = spin
- = total angular momentum
- = theoretical spin of the nucleus
Often though a single valence nucleon determines the total angular momentum of a nucleus. In some cases the total angular momentum is determine by two valence nucleons.
At other times the total angular momentum is given by the combination
Magneton
- Bohr Magnton
- Nuclear Magnton
Nuclear Magnetic moment
Magnetic Dipole Moment
Classical magnetic dipole moment was found by looking at the torque on a current carrying wire of area A carrying a current i and immersed in an external magetic field
If you consider a particle of charge e moving in a circular orbit of radius r then
- : nuclear model
Bulk effects involving magnetism are usually determined by electrons (atomic magnetism). Only in special cases (NMR/MRI) can you see nuclear magnetism.
Spin Magnetic moment
Dirac Equation for point particles.
(electron) = 2.0023
Perhaps the proton and neutron are not point particles!
Fermi Momentum
Fermi Momentum/Energy represents the amount of energy a nucleon (proton or neutron) has when confined to a nucleus. One way to determine this energy is to approximate the nucleus as a 3-D infinite potential well in the form of a cube of side L.
From the 1-D infinite potential well problem you have the eigenfunctions (wave functions) and eigenvalues:
with being a positive integer of quantization.
The three dimensions are independent and thus separable allowing the total wave function and energy eigenvalues to be written as:
where
Now add N non-interacting, spin 1/2 fermions into this box.
- Note
- An atom with atomic number identified by the Chemical symbol with protons has neutrons is denoted as
- in this case N = A = number of nucleons (fermions) in the system (box).
The nucleons in the system occupy occupy the lowest energy state () which forms a sphere in momentum space of radius .
In this ground state the number of nucleons () is equal to the number of states within the sphere of radius in momentum space. In momentum space, the quantum numbers (n_x, n_y, and n_z) are all positive integers. This means that only 1/8 of the sphere is occupied. Each state can hold 2 spin 1/2 nucleons and still obey the Pauli principle.
- Volume of sphere =
or
so the Fermi energy is given by
Which results in a relationship between the fermi energy and the number of particles per volume (when we replace L2 with V2/3):
Fermi Momentum
The total energy of a Fermi sphere of fermions is given by
The Nuclear size/radius of the nucleus is roughly:
- m
- where A is the number of nucleons.
The number density of nucleons in a nucleus is therefore:
So the fermi energy of a nucleus is about:
or
Note: in reality the neutrons and protons are independent systems so I have over counted the total energy when integrating over A.