Difference between revisions of "G4Beamline PbBi"

From New IAC Wiki
Jump to navigation Jump to search
Line 12: Line 12:
  
  
−
A 10 MeV electron beam with a radius of 0.5 cm was incident on a 2 mm thick PbBi target.  The target is positioned at Z = -902 mm.  The plot below shows the energy deposited in MeV along the pipe.  The Z axis is along the beam direction.  The distance around the beam pipe is determine by taking the pipe radius (34.8 mm) and multiplying it by the Phi angle around the pipe.  The bins are 1cm x 1cm.
+
A 10 MeV electron beam with a radius of 0.5 cm was incident on a 2 mm thick PbBi target.  The target is positioned at Z = -902 mm.   
  
  
 +
==Max available power from beam heating==
  
−
+
If you assume a 1mA beam then the beam power incident on the target is
−
{| border="1"
 
−
| [[File:BeamPipeDepEPhi_34.8_082815.png |200px]] ||[[File:BeamPipeDepE_34.8_082815.png| 200 px]]
 
−
|+ A maximum of 450,000 MeV is deposited in a 1 cm<math>^2</math> bin when 20 Million , 10 MeV electrons are incident on a 2 mm thick PbBi target located at Z=-902 mm.
 
−
|}
 
−
 
 
  
 
Beam Power = E(MeV) <math> \cdot </math>I (<math>\mu</math> A) = 10 MeV <math>\times</math> 1000 mA = 10 kW
 
Beam Power = E(MeV) <math> \cdot </math>I (<math>\mu</math> A) = 10 MeV <math>\times</math> 1000 mA = 10 kW
  
−
If all of the beam power goes into a 100 cm long beam pipe with a radius of 3.38 cm then the power deposited per area would be  
+
If the beam does not interact with the target and all the beam power goes into a 100 cm long beam pipe with a radius of 3.38 cm then the power deposited per area would be  
  
 
:<math>10000 \mbox{W}  \times \frac{1}{100 \mbox{cm}}\times \frac{1}{2 \pi \times 3.48 \mbox {cm} } = 4.6 \frac{\mbox{W}}{\mbox{cm}^2}</math>  
 
:<math>10000 \mbox{W}  \times \frac{1}{100 \mbox{cm}}\times \frac{1}{2 \pi \times 3.48 \mbox {cm} } = 4.6 \frac{\mbox{W}}{\mbox{cm}^2}</math>  
  
−
Projections onto the Z-axis
+
==Heating along  the Z-axis==
  
 
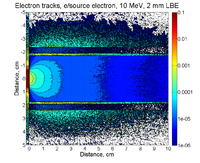
GEANT4 predicts that scattered electrons, photons, and positrons (mostly scattered electrons) deposit
 
GEANT4 predicts that scattered electrons, photons, and positrons (mostly scattered electrons) deposit
Line 69: Line 65:
  
  
 +
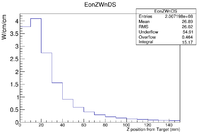
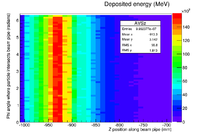
The plot below shows the energy deposited in MeV along the pipe.  The Z axis is along the beam direction.  The distance around the beam pipe is determine by taking the pipe radius (34.8 mm) and multiplying it by the Phi angle around the pipe.  The bins are 1cm x 1cm.
 +
 +
 +
 +
 +
{| border="1"
 +
| [[File:BeamPipeDepEPhi_34.8_082815.png |200px]] ||[[File:BeamPipeDepE_34.8_082815.png| 200 px]]
 +
|+ A maximum of 450,000 MeV is deposited in a 1 cm<math>^2</math> bin when 20 Million , 10 MeV electrons are incident on a 2 mm thick PbBi target located at Z=-902 mm.
 +
|}
  
 
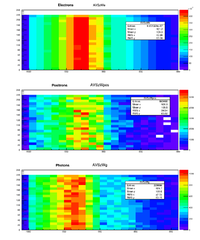
Below is energy deposited contributions from from photons(AVSzWg), positrons (AVSzWpos), and electrons.
 
Below is energy deposited contributions from from photons(AVSzWg), positrons (AVSzWpos), and electrons.

Revision as of 20:34, 31 August 2015

Development of a Positron source using a PbBi converter and a Solenoid

Task List

1.) new electron and positron files for the case of two 0.25 mm thick SS windows around the PbBi target.

2.) Determine electron energy deposition in SS pipe per cm^2 of pipe surface area for pipes with a radius of 34.8, 47.5, 60.2, 72.9, and 97.4 mm and thickness of 5mm along the z-axis.

3.) Insert uniform B-field that can be scaled from 0 to 0.3 and 1 Telsa.

Beam Pipe Heating

A 10 MeV electron beam with a radius of 0.5 cm was incident on a 2 mm thick PbBi target. The target is positioned at Z = -902 mm.


Max available power from beam heating

If you assume a 1mA beam then the beam power incident on the target is

Beam Power = E(MeV) [math] \cdot [/math]I ([math]\mu[/math] A) = 10 MeV [math]\times[/math] 1000 mA = 10 kW

If the beam does not interact with the target and all the beam power goes into a 100 cm long beam pipe with a radius of 3.38 cm then the power deposited per area would be

[math]10000 \mbox{W} \times \frac{1}{100 \mbox{cm}}\times \frac{1}{2 \pi \times 3.48 \mbox {cm} } = 4.6 \frac{\mbox{W}}{\mbox{cm}^2}[/math]

Heating along the Z-axis

GEANT4 predicts that scattered electrons, photons, and positrons (mostly scattered electrons) deposit


BeamPipeDepEmev 34.8 082915.png
Energy deposited (MeV) in a 1 m long 3.48 cm radius beam pipe surrounding a 2 mm target located at Z=-902 mm when 20 million electrons impinge the target.

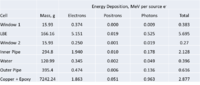
According to the above figure, GEANT4 predicts a total of [math]1.064 \times 10^7[/math] MeV (the integral adds up the energy in each 1cm bin) of energy will be deposited in a 1m long beam pipe surrounding a 2 mm thick PbBi target located at Z=-902 mm when 20 million electrons impinge the target.

If this energy were uniformly distributed this energy along the 0.5 mm thick beam pipe having a radius of 3.48 cm then I would see

[math]1.06 \times 10^{10} \mbox{keV} \times \frac{1}{100 \mbox{cm}}\times \frac{1}{2 \pi \times 3.48 \mbox {cm} } \times \frac{1}{2 \times 10^7 \mbox{e}^-}=0.24\frac{\mbox{keV}}{\mbox{cm}^2 \;\;\mbox{e}^-}[/math]


if you assume a 1 mA beam of electrons then this becomes

[math]\left ( \frac{0.24 \; \mbox{W} }{ \mbox{cm}^2 } \right) [/math]


If you use the above factors to weight the histogram, then the figure below shows that GEANT4 predicts a power deposition density of [math]= 0.15 \frac{W}{cm^2}[/math], 3 cm downstream of the target. Back scattered electrons appear to create the hottest spot of [math]= 0.53 \frac{W}{cm^2}[/math] about 3cm upstream of the target.

BeamPipeDepE 34.8mmA 082815.png BeamPipeDepE 34.8mmB 082815.png
Power Depositrion Zoomed in and 902 mm offset applied Power deposition over the 1 m long beam pipe

I converted the above histogram to deposited power you would divide by the number of incident electrons, divide by the circumference of the beam pip, multiple the beam current, and use a unit conversion from MeV to W-s per MeV.

[math]\left(Counts \frac{\mbox{MeV}}{\mbox{cm}}\right) \times \left( \frac{1}{2 \times 10^{7} \mbox{e}^-} \right ) \times \left( \frac{1}{2 \times \pi \times 3.48 \mbox{cm}} \right ) \times \left( \frac{1. \times 10^{-3}\mbox{ C}}{\mbox{s} }\right )\times \left( \frac{\mbox{e}^- }{1.6 \times 10^{-19}\mbox{ C}}\right ) \left( \frac{1.6 \times 10^{-13}\mbox{W} \cdot \mbox{ s}}{\mbox{MeV} }\right ) \times [/math]


The plot below shows the energy deposited in MeV along the pipe. The Z axis is along the beam direction. The distance around the beam pipe is determine by taking the pipe radius (34.8 mm) and multiplying it by the Phi angle around the pipe. The bins are 1cm x 1cm.



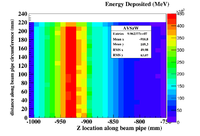
BeamPipeDepEPhi 34.8 082815.png BeamPipeDepE 34.8 082815.png
A maximum of 450,000 MeV is deposited in a 1 cm[math]^2[/math] bin when 20 Million , 10 MeV electrons are incident on a 2 mm thick PbBi target located at Z=-902 mm.

Below is energy deposited contributions from from photons(AVSzWg), positrons (AVSzWpos), and electrons.


BeamPipeDepE 34.8 082815 parttype.png

Why is the positron hotspot upstream of the target?



root commands used 

TH2D *AVSz=new TH2D("AVSz","AVSz",100,-1000,0,12,-60,60)
BeamPipeE->Draw("35.*atan(PosYmm/PosXmm):PosZmm>>AVSz","DepEmeV"); 
AVSz->Draw("colz");


BeamPipeHeating_4mmthick_PbBi_PositronTarget

Unit conversion

The energy deposited by photon, electrons, and positrons is predicted by GEANT4 and recorded in energy units of keV per incident electron on the PbBi target. To convert this deposited energy to a power you need to assume a beam current. Assuming 1 beam current of 1 mA, the conversion is given easily as

[math]\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) \times \left( \frac{ \mbox{e}^-}{1.6 \times 10^{-19}\mbox{C}} \right ) \times \left( \frac{1 \times 10^{-3} \mbox{C}}{\mbox{s}} \right ) \times \left( \frac{1.6 \times 10^{-16}\mbox{W} \cdot \mbox{ s}}{\mbox{keV} }\right )[/math]

[math]\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) = \left( \frac{\mbox{W} }{\mbox{cm}^2 } \right )[/math]

Results Table

Beam Pipe Radius (mm) Hot Spot ([math]keV/cm^2/e^-[/math])
34.8 5
47.5
60.2
72.9
97.4

Converter target properties

Definition of Lead Bismuth


1cm diameter target 2 mm thick PbBi

0.5 Tesla solenoid


Desire to know

Emmittance (mrad * mm)

dispersion (Delta P/P) (mradian/1000th mm/1000th)

of electrons after the PbBi target.


pole face rotation in vertical plane.

G4BeamLine and MCNPX

Target thickness optimization

PbBi_THickness_GaussBeam

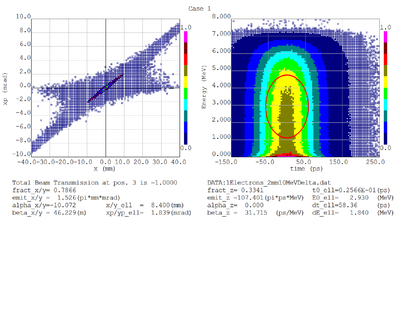
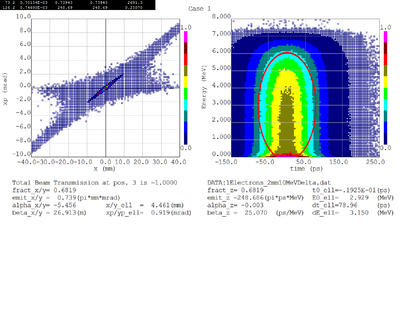
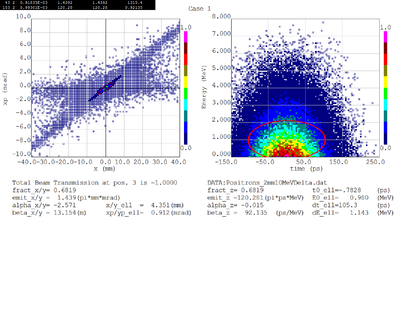
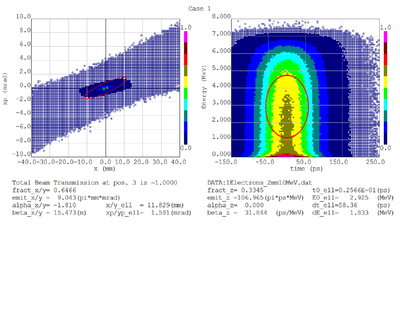
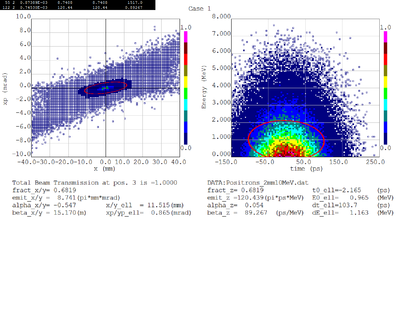
Dmitry's processing of Tony's GEANT simulations showing transverse phase space portrait (left) and longitudinal phase space portrait (right). Phase space portraits show coordinate x or y vs diveregense=px/pz or py/pz (or time vs kinetic energy ). Captions show:

1. geometric (not normalized) emittance for transverse and emittance for longitudinal phase space portraits (ellipse areas divided by "pi")

2. Twiss parameters

3. Ellipse centroid for longitudinal phase portrait

4. sqrt(beta*emittance) and sqrt(gamma*emittance) - half sizes of the projections of the ellipses on the coordinate and divergence axes respectively.

Electrons - RMS

Ed1.png

Electrons - 68.2% core

Ed2.png

Positrons - RMS

Pd1.png

Positrons - 68.2% core

Pd2.png

PbBi_THickness_CylinderBeam

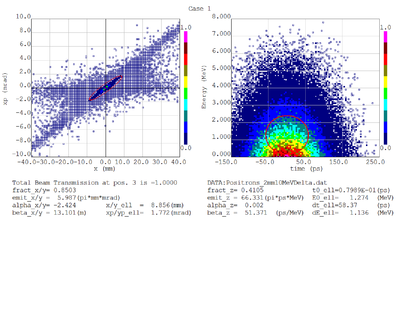
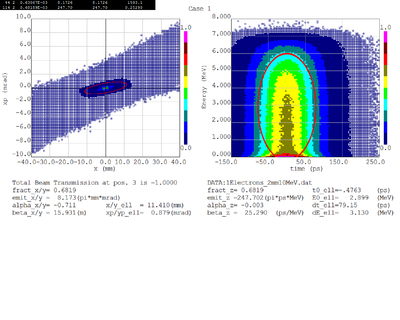
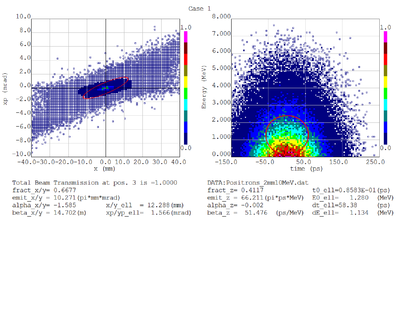
Dmitry's processing of Tony's GEANT simulations showing transverse phase space portrait (left) and longitudinal phase space portrait (right). Phase space portraits show coordinate x or y vs diveregense=px/pz or py/pz (or time vs kinetic energy ). Captions show:

1. geometric (not normalized) emittance for transverse and emittance for longitudinal phase space portraits (ellipse areas divided by "pi")

2. Twiss parameters

3. Ellipse centroid for longitudinal phase portrait

4. sqrt(beta*emittance) and sqrt(gamma*emittance) - half sizes of the projections of the ellipses on the coordinate and divergence axes respectively.

Electrons - RMS

E1.png

Electrons - 68.2% core

E2.png

Positrons - RMS

P1.png

Positrons - 68.2% core

P2.png

PbBi_THickness_PntSource

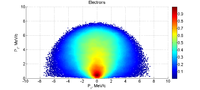
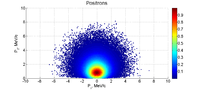
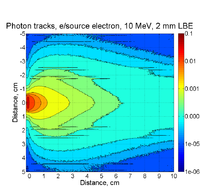
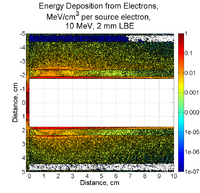
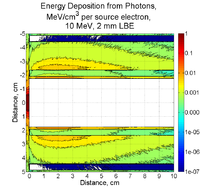
Electrons and Positrons after 2mm of LBE:

Electrons:

E01.pngE02.png

Positrons:

P01.pngP02.png

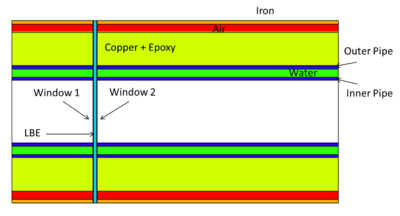
Energy Deposition in Target system (Heat)

ElectronTracks.pngPhotonTracks.png

ElectronEnergy.pngPhotonEnergy.png

MCNPX simulations of energy deposition into different cells are below. There is a slight overestimate (they add up to about 120%). Positrons contribute less than 1% of electrons' contribution. No magnetic filed is assumed.

Model.png

Tablen1.png

Tablen2.png

Solenoid

Inner Radiusu=

Outer Radius =

Length =

Current=

Magnetic Field Map in cylindrical coordinates (Z & R) from Niowave

Beam Line Design

PbBi_BeamLine_Elements

goals for JLab

Positrons#Simulations

Retrieved from "https://wiki.iac.isu.edu/index.php?title=G4Beamline_PbBi&oldid=101628"