G4Beamline PbBi

Development of a Positron source using a PbBi converter and a Solenoid

Task List

1.) new electron and positron files for the case of two 0.25 mm thick SS windows around the PbBi target.

2.) Determine electron energy deposition in SS pipe per cm^2 of pipe surface area for pipes with a radius of 34.8, 47.5, 60.2, 72.9, and 97.4 mm and thickness of 5mm along the z-axis.

3.) Insert uniform B-field that can be scaled from 0 to 0.3 and 1 Telsa.

Beam Pipe Heating

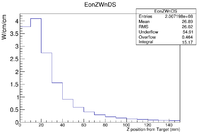
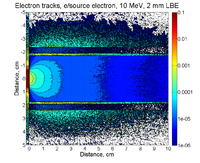
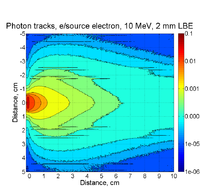
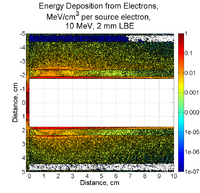
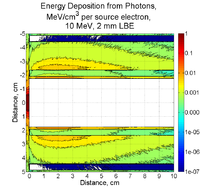
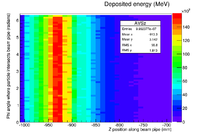
A 10 MeV electron beam with a radius of 0.5 cm was incident on a 2 mm thick PbBi target. The target is positioned at Z = -902 mm. The plot below shows the energy deposited in MeV along the pipe. The Z axis is along the beam direction. The distance around the beam pipe is determine by taking the pipe radius (34.8 mm) and multiplying it by the Phi angle around the pipe. The bins are 1cm x 1cm.

About 450,000 MeV/cm^2 is deposited when 20 Million , 10 MeV electrons are incident on a 2 mm thick PbBi target located at Z=-902 mm.

Beam Power = E(MeV) [math] \cdot [/math]I ([math]\mu[/math] A) = 10 MeV [math]\times[/math] 1000 mA = 10 kW

If all of the beam power goes into a 150 cm long beam pipe with a radius of 3.38 cm then the power deposited per area would be

[math]10000 \mbox{W} \times \frac{1}{150 \mbox{cm}}\times \frac{1}{2 \pi \times 3.48 \mbox {cm} } = 3 \frac{\mbox{W}}{\mbox{cm}^2}[/math]

Projections onto the Z-axis

Energy deposited (MeV) in a 1 m long 3.48 cm radius beam pipe surrounding a 2 mm target located at Z=-902 mm when 20 million electrons impinge the target.

According to the above figure, GEANT4 predicts a total of [math]1.064 \times 10^7[/math] MeV of energy will be deposited in a 1m long beam pipe surrounding a 2 mm thick PbBi target located at Z=-902 mm when 20 million electrons impinge the target. [math]\left( \frac{1.064 \times 10^7\mbox{MeV}}{2 \times 10^7 \mbox{e}^-}\right) = \frac{500\mbox{keV} }{\mbox{e}^- }[/math]

If all of this energy were UNIFORMLY distriuted along the 3.48 cm radius pipe then the energy deposited per area would be

[math]\left(\frac{ 500 \mbox{keV}}{100 \times 2 \pi \times 3.48 \;\; \mbox{cm}^2 \;\; \mbox{e}^-}\right) \sim \frac{0.23 \; \mbox{keV} }{ \mbox{cm}^2\;\; \mbox{e}^- }[/math]

if you assume a 1 mA beam of electrons then this becomes

[math]\left ( \frac{0.23 \; \mbox{W} }{ \mbox{cm}^2 } \right) [/math]

GEANT4 predicts a power deposition density of [math]= 0.76 \frac{W}{cm^2}[/math], 3 cm downstream of the target. The total power density deposited on a 1 m long beam pipe is [math]= 24 \frac{W}{cm^2}[/math]. Back scattered electrons appear to creat the hottest spot of [math]= 2.6 \frac{W}{cm^2}[/math] about 3cm upstream of the target.

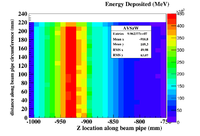
I converted the above histogram to deposited power you would divide by the number of incident electrons, divide by the circumference of the beam pip, multiple the beam current, and use a unit conversion from MeV to W-s per MeV.

[math]\left(Counts \frac{\mbox{MeV}}{\mbox{cm}}\right) \times \left( \frac{1}{2 \times 10^{7} \mbox{e}^-} \right ) \times \left( \frac{1}{2 \times \pi \times 3.48 \mbox{cm}} \right ) \times \left( \frac{1. \times 10^{-3}\mbox{ C}}{\mbox{s} }\right )\times \left( \frac{\mbox{e}^- }{1.6 \times 10^{-19}\mbox{ C}}\right ) \left( \frac{1.6 \times 10^{-13}\mbox{W} \cdot \mbox{ s}}{\mbox{MeV} }\right ) \times [/math]

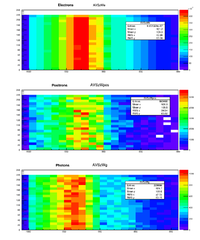
Below is energy deposited contributions from from photons(AVSzWg), positrons (AVSzWpos), and electrons.

Why is the positron hotspot upstream of the target?

root commands used

TH2D *AVSz=new TH2D("AVSz","AVSz",100,-1000,0,12,-60,60)
BeamPipeE->Draw("35.*atan(PosYmm/PosXmm):PosZmm>>AVSz","DepEmeV"); 
AVSz->Draw("colz");

BeamPipeHeating_4mmthick_PbBi_PositronTarget

Unit conversion

The energy deposited by photon, electrons, and positrons is predicted by GEANT4 and recorded in energy units of keV per incident electron on the PbBi target. To convert this deposited energy to a power you need to assume a beam current. Assuming 1 beam current of 1 mA, the conversion is given easily as

[math]\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) \times \left( \frac{ \mbox{e}^-}{1.6 \times 10^{-19}\mbox{C}} \right ) \times \left( \frac{1 \times 10^{-3} \mbox{C}}{\mbox{s}} \right ) \times \left( \frac{1.6 \times 10^{-16}\mbox{W} \cdot \mbox{ s}}{\mbox{keV} }\right )[/math]

[math]\left( \frac{\mbox{keV}}{\mbox{cm}^2 \mbox{e}^-}\right) = \left( \frac{\mbox{W} }{\mbox{cm}^2 } \right )[/math]

Results Table

Beam Pipe Radius (mm)	Hot Spot ([math]keV/cm^2/e^-[/math])
34.8	5
47.5
60.2
72.9
97.4

Converter target properties

Definition of Lead Bismuth

1cm diameter target 2 mm thick PbBi

0.5 Tesla solenoid

Desire to know

Emmittance (mrad * mm)

dispersion (Delta P/P) (mradian/1000th mm/1000th)

of electrons after the PbBi target.

pole face rotation in vertical plane.

G4BeamLine and MCNPX

Target thickness optimization

PbBi_THickness_GaussBeam

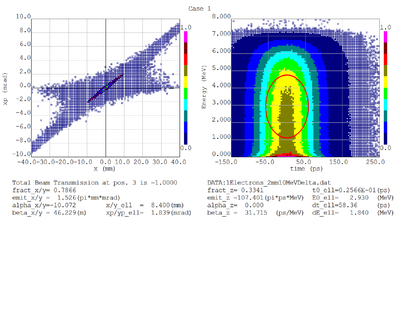
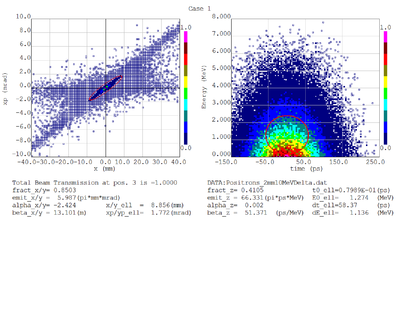
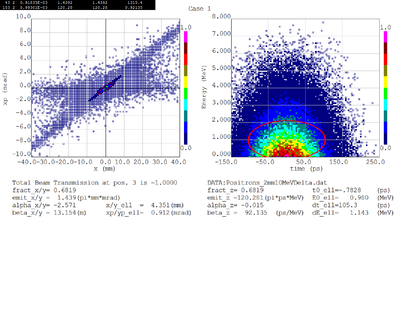
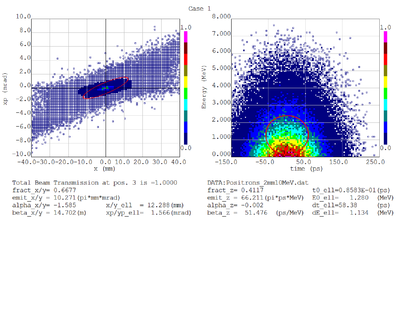
Dmitry's processing of Tony's GEANT simulations showing transverse phase space portrait (left) and longitudinal phase space portrait (right). Phase space portraits show coordinate x or y vs diveregense=px/pz or py/pz (or time vs kinetic energy ). Captions show:

1. geometric (not normalized) emittance for transverse and emittance for longitudinal phase space portraits (ellipse areas divided by "pi")

2. Twiss parameters

3. Ellipse centroid for longitudinal phase portrait

4. sqrt(beta*emittance) and sqrt(gamma*emittance) - half sizes of the projections of the ellipses on the coordinate and divergence axes respectively.

Electrons - RMS

Electrons - 68.2% core

Positrons - RMS

Positrons - 68.2% core

PbBi_THickness_CylinderBeam

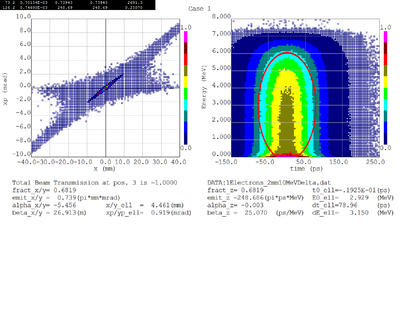
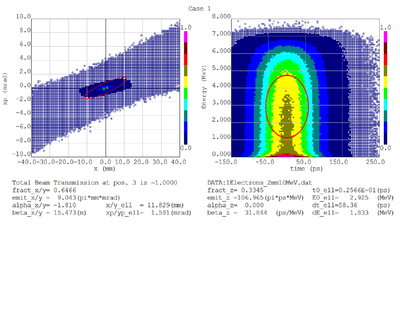
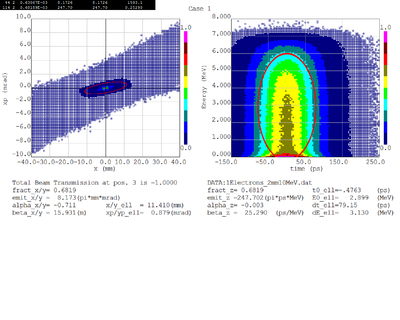
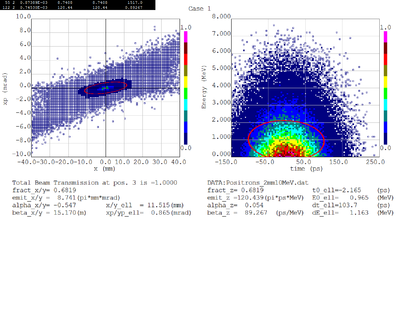
Dmitry's processing of Tony's GEANT simulations showing transverse phase space portrait (left) and longitudinal phase space portrait (right). Phase space portraits show coordinate x or y vs diveregense=px/pz or py/pz (or time vs kinetic energy ). Captions show:

1. geometric (not normalized) emittance for transverse and emittance for longitudinal phase space portraits (ellipse areas divided by "pi")

2. Twiss parameters

3. Ellipse centroid for longitudinal phase portrait

4. sqrt(beta*emittance) and sqrt(gamma*emittance) - half sizes of the projections of the ellipses on the coordinate and divergence axes respectively.

Electrons - RMS

Electrons - 68.2% core

Positrons - RMS

Positrons - 68.2% core

PbBi_THickness_PntSource

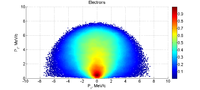
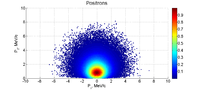
Electrons and Positrons after 2mm of LBE:

Electrons:

Positrons:

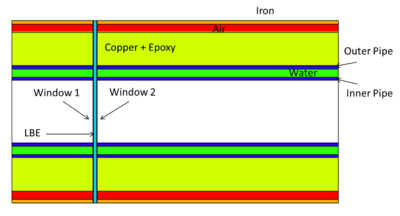
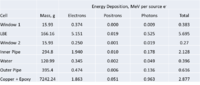
Energy Deposition in Target system (Heat)

MCNPX simulations of energy deposition into different cells are below. There is a slight overestimate (they add up to about 120%). Positrons contribute less than 1% of electrons' contribution. No magnetic filed is assumed.

Solenoid

Inner Radiusu=

Outer Radius =

Length =

Current=

Magnetic Field Map in cylindrical coordinates (Z & R) from Niowave

Beam Line Design

PbBi_BeamLine_Elements

goals for JLab

Positrons#Simulations