Difference between revisions of "Gaseous Medium Physical Concepts"

From New IAC Wiki
Jump to navigation Jump to search
 
(36 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
=Related Physical Concepts=
 
=Related Physical Concepts=
  
−
The gaseous medium inside a detector's chamber contains different physical processes as a particle arrives the gas in the chamber. When the desired the particles penetrate the gaseous medium, they directly or indirectly (neutron '''''fission''''')  '''''ionize''''' the gas. If the event happened in the active detection area of the detector, a drift '''''electric field''''' guides the primary and secondary electrons toward the GEM preamplifiers, they are placed to have a separation distance within the maximum limit to not lose the electrons by '''''diffusion''''', and to '''''multiply''''' the number of electrons to create an avalanche directed toward the read out plate which collects the electrons to appear as a negative pulse on the oscilloscope. Electron '''''recombination''''', '''''deattachment''''' and '''''capture'''''  take place in every stage in the electron trip before they reach the readout plate, especially in case of the gas' pressure is higher than the atmospheric pressure. Also, the preamplifiers may have  ''discharge'' events on their surfaces that usually damage them.
+
The gaseous medium inside a detector's chamber contains different physical processes as a particle arrives the gas. When the desired particles penetrate the gaseous medium, they directly or indirectly (neutron '''''fission''''')  '''''ionize''''' the gas. If the event happened in the active detection area of the detector, a drift '''''electric field''''' guides the primary and secondary electrons toward the GEM preamplifiers, These preamplifiers are placed to have a separation distance within a limit to not lose the electrons by keeping their '''''diffusion''''' to be a reason for their '''''multiplication''''' . An electron  avalanches appear and the negative voltage directs them toward the read out plate which collects the electrons to show them as negative pulses on the oscilloscope's screen. Electron '''''recombination''''', '''''deattachment''''' and '''''capture'''''  take place in every stage in the electron trip before they reach the readout plate. The output signal is important to measure the detector's performance by determining its efficiency, dead time, gain, spatial resolution and robustness.Theoretically, the detector output can be evaluated by solving Boltzmann equation that considers the effect of each physical process occurred.
  
−
The detector pulse is evaluated by a mathematical  description to each physical process that occurs in any stage to count the number of the electrons' pulse. Measuring the output of helps in calculating the detector    efficiency, dead time, gain, spatial resolution and robustness.
 
  
−
 
 
==Ionization==
 
==Ionization==
  
−
Ionization is the liberation of an electron from the confines of a medium atoms or molecules. Also the minimum amount of energy required to liberate the electron is referred to as the ionization energy.  When the ionizing particle get in the medium, it deposits its energy to free electrons, energy in excess of this ionization energy will appear in the form of kinetic energy carried by the free electrons. For instance, charged particles, like fission fragments, ionizes a gaseous medium and free electrons with  kinetic energy that depends on the fragment energy deposition remained after ionization.  
+
Ionization is the liberation of an electron from the medium's atoms or its molecules. The minimum amount of energy required to liberate the electron is referred to as the ionization energy.  When the ionizing particle gets in the medium, it deposits its energy to scatter free electrons which they get their kinetic energy after losing part of their energy in releasing from the atom confinement, and after passing through electron-electron collisions. For instance, charged particles like fission fragments ionizes the medium and scatter free electrons, the kinetic energy depends on the fission fragment's energy gained after ionization and the number of collisions the electron passes through.  
 +
 
 +
The ionization is a stochastic process, it depends on the ionization cross section that is determined by the ionizing particle energy, and mass(heavy or light in case of fission fragments). However, the amount of energy needed to have an ionization event on average is the same, regardless of the incident particle type or energy as shown in the following table for argon gas.<ref name="Veenhof"> R. Veenhof, Internal Note/TPC, ALICE-INT-2003-29 version 1.0, 2003</ref>
  
−
The ionization process  depends stochastically  on the ionization cross section which is usually determined by the ionizing particle energy, and mass( heavy or light in case of fission fragments), but it is observed that  the amount of energy needed to have an ionization event in a gas is the same on average  <ref name="Veenhof"> R. Veenhof, Internal Note/TPC, ALICE-INT-2003-29 version 1.0, 2003</ref>, regardless of the incident particle type or energy as shown in the following table for argon gas.
 
  
 
{| border="1" cellpadding="4"
 
{| border="1" cellpadding="4"
Line 21: Line 20:
 
===Ionization in fission chambers===
 
===Ionization in fission chambers===
  
−
Ionization by fission fragment is not  the only source for a electrons and it  is not the only ionization process in fission chamber. These chambers basically contain a neutoron fissinable material; it is a heavy radioisotope that decays and emits more than one type of the ionizing radiation by the radioisotope itself or by its daughters. For instance, using U-233, the source for the free electrons are fission fragments, alpha particles, beta particles, and gamma rays. More specific details about U-233 decay products is shown by the following tables.
+
Ionization by a fission fragment is not  the only source for free electrons and it  is not the only ionization process in fission chamber. Fission chambers usually contain neutoron fissinable materials, they are heavy radioisotopes that decay and emit more than one type of the ionizing radiation or by their daughters after decay. For instance, when the fission chamber contains U-233, free electrons are detected because of escaping fission fragments, alpha particles, beta particles, or gamma rays. More specific details about U-233 decay products is shown by the following tables:
  
 
{| border="1" cellpadding="4"
 
{| border="1" cellpadding="4"
Line 58: Line 57:
 
|}
 
|}
  
−
To count the free electrons produced by the fission fragments demands some modifications in the detector design which will be mentioned in details in the detector construction section .
+
To count the free electrons produced by the fission fragments demands some modifications in the detector design which mentioned in details in detector construction section .
  
−
They are other  physical processes occur in the medium which are related to the gas mixture properties such as: photoionization, thermal ionization, deionization by attachment (negative ion formation) , photoelectric emission, electron emission by excited atoms or positive ion,penning ,and field emission <ref name="Kuffel"/>. The previos processes probably share in decreasing or increasing the number of free electrons in the medium, so evaluating the number of free electrons before amplification becomes sophisticated processes without a computer simulation.
+
They are other  physical processes occur in the medium which are related to the gas mixture properties such as: photoionization, thermal ionization, deionization by attachment (negative ion formation) , photoelectric emission, electron emission by excited atoms or positive ion,penning ,and field emission <ref name="Kuffel"/>. The previous processes may share in decreasing or increasing the number of free electrons in the medium, so evaluating the number of free electrons before preamplification becomes sophisticated without a computer simulation.
  
  
 
Garfield simulates the ionization in the gas mixture cosidering all the former physical processes, it has the ability to simulate the electrons multiplication by GEM preaplifiers, it accepts external solutions for the electric field by other software packages like ANSYS, and it has more than one package such as  Magboltz, HEED, and  Imonte 4.5 that can be used for more precise simulations <ref name="Veenhof"/>.
 
Garfield simulates the ionization in the gas mixture cosidering all the former physical processes, it has the ability to simulate the electrons multiplication by GEM preaplifiers, it accepts external solutions for the electric field by other software packages like ANSYS, and it has more than one package such as  Magboltz, HEED, and  Imonte 4.5 that can be used for more precise simulations <ref name="Veenhof"/>.
  
−
===Why 90/10 Ar/CO2 Mixture and why Garfield <ref name="Veenhof"/>===
+
=Diffusion=
−
;why Garfield
 
−
 
 
−
Garfield is the most commonly used by CERN for simulating the gaseous detectors. It contains two other software packages:
 
−
 
 
−
- HEED (high energy electrodynamics):it is used for Estimating the number of electrons produced by ionization for an incident particle (a charged particle in our case). HEED uses PAI model (Photoabsorption ionization)which describes the relationship between the energy deposited by the charged particle and the photoabsorption cross section of the gas atom "not with a single electron or particular atomic shell" to simulate the initial ionization. HEED considers the cross section for individual shells of the atom or the molecules that build the gaseous medium. <ref name="Smirnov"> NIM A 554 2005 474-493</ref>
 
−
 
 
−
- Magboltz: It provides an accurately calculated drift velocity for the electron, it considers the existence of the electric field and the magnetic field, the solution for the transport equation to more than two terms, Lengo and Capitelli technique that allows using the the elastic and inelastic collisions using the momentum transfer inelastic cross section, isotropic foraward and backward scattering using the random numbers,
 
−
 
−
* Drift velocity: Increasing the percentage of CO2 the gas mixture at low electric field increases the drift velocity as shown in the figure:
 
−
 
 
−
[[File:drift_velocity_percentage_CO2_inAr.png || 100px]]
 
−
 
 
−
 
 
−
The drift velocity is saturated but at different values depending the percentage of the CO2, so the increase in the drift velocity becomes smaller withe increase in CO2 percentage int he gas mixture as show in the figures below:
 
−
 
 
−
[[File:max_drift_velocity_CO2percent_Efieldvalue.png || 100px]]          [[File:Vmax_CO2percent.png || 100px]]
 
−
 
 
−
 
 
−
*Gain: It is dependent on Townsend coefficient, the figure below shows the gain-Electric field relationship for different mixtures of ArCO2, in addition to the effect penning of the gain.
 
−
 
 
−
[[File:Townsend_coeffiecient_inArCO2.png || 100px]]
 
−
 
 
−
The figure above is not accurate enough since Garfield and Magboltz software packages use the first two terms of  Legendre polynomials as solution for Boltzmann transport equation (Magboltz may extend to the third term when the simulation goes in the longer time one), but using using IMonte 4.5 uses the spherical harmonics which improved the simulation and make independent of the expansions that describe the electron energy distribution. <ref name="Biagi"> S.Biagi Nucl. Instrum. Methods, vol. A 421, pp. 234–240, 1999</ref >
 
−
 
 
−
The effect of Penning on Townsend coefficient is represented by the following :
 
−
 
 
−
[[File:Townsend_coefficient_inArCO2_Penning.png || 100px]]
 
−
 
 
−
Comparing Ne/CO2 with Ar/CO2 considering the 40 percent of Penning transfer:
 
−
 
 
−
[[File:gain_NeCO2_ArCO2_full_40percent_penning_transfer.png || 100px]]
 
−
 
 
−
*Ionization rate:
 
−
 
 
−
[[File:ArCO2_ionization_rate.png || 100px]]
 
−
 
 
−
*Attachment:
 
−
 
 
−
[[File:ArCO2_attachment_Efieldvalue.png || 100px]]    [[File:ArCO2_attachment_losspercent_anodevoltage.png || 100px]]
 
−
 
 
−
==Diffusion==
 
−
 
 
−
Charged particles diffusion in gas is defined  as <ref name="Mason"/> the "disperse" of the particles in a gas
 
−
"in which there is a net spatial transport" of the charged particles "produced by the gradient in their relative concentrations". Assuming that the charged particles are localized in a gas with a uniform temperature, pressure and has low '''n''' charged particle density to ignore Coulomb force.
 
−
       
 
−
<math> J = -D \nabla n </math>
 
−
 
 
−
where ''D'' is the diffusion coefficient and '''J''' is the number of the charged particle flow per unit time.
 
−
 
 
−
Maxwell Boltzmann equation solution describes  ''n'' as a function of position '''r''' and time ''t'',  In our case, ''n'' represents the number electrons propagating in presence of an electric field. Maxwell Boltzmann equation is "the equation of continuity for the population ''n'' ''f'' d'''r''' d'''c''' " where ''f'' is velocity distribution function.
 
−
The equation includes the loss of electrons as they transport across a surface boundary in a volume element d'''r'''
 
−
, and the effect of the electric field (uniform in our case) in accelerating  each ''n''
 
−
d'''r''' electrons which changes
 
−
d'''c'''  from point to another in the phase space so the number of point loss in a time
 
−
d''t'' is
 
−
<math> dt \nabla ._{c}(\frac{n f  e E}{m}) dc dr </math>,
 
−
in addition to the loss of points <math>\Delta</math>''n'' in d'''c''' as result of the quasi discontinuous change in position <math>\Delta</math>'''c''' in velocity space as the electron meets a molecule.
 
−
 
−
So Maxwell Boltzmann equation can be written as based on the previous assumptions as the following:<ref name="Huxley"> Huxley, L. G. H. Leonard George Holden, The diffusion and drift of electrons in gases, John Wiley and sons, 1974 , call number QC793.5.E628 H89 </ref>
 
−
 
 
−
<math> \frac {\partial{} }{\partial{t}}</math>(''nf'') +
 
−
<math>\nabla._{r}</math>(''n'' ''f'' '''c''') +
 
−
<math>\nabla._{c}</math> (''n'' ''f''
 
−
<math>\frac{e E}{m})</math>+ S = 0
 
−
 
 
−
The previous equation can be written in terms of the diffusion coefficients and the average velocity of the electrons and it is called the scalar equation of Maxwell Boltzmann equation:
 
−
 
 
−
<math> \frac {\partial{} }{\partial{t}}(nf_0)</math> +
 
−
<math>\frac{c}{3}\nabla._{r}</math> (''n'' '''f_1''')+
 
−
<math>\frac{1}{4\pi c^2}\frac{\partial {}}{\partial{c}} (\sigma_E - \sigma_{coll}) = 0 </math>
 
−
 
 
−
===Assumptions: <ref name="Huxley"/>=== 
 
−
 
 
−
;Velocity Shells
 
−
 
 
−
The electrons are distributed in the phase space in velocity shell of mean velocity '''W''' represented by the following equation
 
−
 
 
−
<math> W = \frac {\sum_c n_c W(c)}{n dr} </math>
 
−
 
 
−
Where '''W'''(c) is the resultant velocity of the of the velocities of the electrons in the velocity shell 4<math>\pi c^2 sin\theta dc d\theta d\phi </math>, so the population of velocity points in the shell is represented by the n d'''r''' <math> [c^2 dc] [f(c,\theta,r,t)sin\theta dc d\theta d\phi] </math>. it is assumed for a velocity shell the following distribution function:
 
−
 
 
−
<math> f(c,\theta,r,t) =  f_0(c,\theta,r,t) + \sum_{k=0} ^\infty  f_k(c,\theta,r,t) P_k (cos\theta)</math>
 
−
 
−
 
 
−
<math>P_k (cos\theta)</math> is the Legendre polynomial of order k. In the case the mean velocity is independent of the azimuthal angle then its magnitude can be determined by the following:
 
−
 
 
−
<math> W(c) = \frac{1}{n_c} (ndr) c^2 dc \int_0^\pi \int_0^{2\pi}(f_0 +\sum_1^\infty  f_k P_k (cos\theta)) c \, cos\theta sin\theta d\theta d\phi  = \frac {cf_1}{3f_0}</math>
 
−
 
 
−
and the population desity point is :
 
−
 
 
−
<math> n_c =  (ndr) c^2 dc \int_0^\pi \int_0^{2\pi}(f_0 +\sum_1^\infty  f_k P_k (cos\theta))  sin\theta d\theta d\phi  = n f_0 4\pi c^2 dc dr</math>
 
−
 
 
−
So the mean velocity is evaluated  depending on the former definition is :
 
−
 
 
−
<math> W = \frac {\sum_c n_c W(c)}{n dr}  = \frac{cf_1}{3f_0}</math>
 
−
 
 
−
It is worth mentioning here that W represent the mean velocity of the electron population and the instantaneous velocity of the of the centroid of ''n''.
 
−
 
 
−
;The loss and the gain in the number of points
 
−
 
 
−
The loss in the number of  points from (''c'',d''c'') is depending on <math> \sigma_E (c) </math> and mathematically can be written as <math> dt dr dc \frac{\partial{}}{\partial{c}}\sigma_E (c) </math>.
 
−
Simultaneously, the gain in the number of points (''c'',d''c'') is evaluated using <math> \sigma_{coll} (c) </math> such that <math> dt dr dc \frac{\partial{}}{\partial{c}}\sigma_{coll} (c) </math> is the gain per unit volume (in phase space) per unit time.
 
−
 
 
−
So the net change in the number of points in the shell is <math> dt dr dc\frac{\partial{}}{\partial{c}}(\sigma_E (c)-\sigma_{coll} (c))  </math>.
 
−
 
 
−
Where  <math> \sigma_{coll} (c) = 4\pi n c^2 \nu_{el} (\frac {m}{M} c f_0 + \frac{\bar{C^2}}{3} \frac{\partial{f_0}}{\partial{c}}) </math>
 
−
and <math> \sigma_E (c) = \frac{4\pi}{3}  c^2 \frac {eE}{m} n f_1 </math>
 
−
, <math> \nu_{el} = Ncq_{el}(c) </math>, N is the molecular density, M is the mass of the molecule,
 
−
<math> q_{el}(c) </math>  is the momentum transfer cross section for elastic encounters.
 
−
and <math> \bar {C^2}</math> is the mean square speed of the molecules.
 
−
 
 
−
;Drift velocity and diffusion coefficients
 
−
 
 
−
The electron density number, diffusion coefficients and drift velocity relationship is studied for a close chamber contained a travelling swam of electrons in a uniform electric field that directed the swarm toward the +z axis. Mathematically the relationship is assumed as the follwoing:
 
  
−
<math> \frac{\partial{}}{\partial{t}}</math>''n'' 
+
;Main differences between electrons and ions behavior in a gas <ref name="Mason">Mason, Edward A. and Earl W. MacDaniel. 1988. Transport Properties of Ions in Gases. John Wiley & Sons. QC717.5 I6 M37 </ref>
−
- ''D'' <math> \nabla^2</math>''n'' )  +
 
−
''W''  <math>\frac{\partial{ }}{\partial{z} }</math> ''n'' = 0
 
  
−
where
+
Studying diffusion and mobility  of  charged particles in a gas is classified in to two main groups, ion and electron diffusion and mobility. They are conceptually similar, but they have many differences. First, The ratio between the mass of the electrons and the gas atoms is very small, so with a few eV work done by the electric field, the electrons will gain a high velocity compared to that of the ions that are accelerated under the same electric field. Also, the probability of low energy electrons to make an interaction is higher than that of the low energy ions, the electron interactions are a supported with accurate calculations for the electron drift velocity. Electrons at low energy have the ability to produce vibrations and excitations in the gas atoms or molecules which are measured within the lab frame, but low energy ions have very low cross sections for most of the interactions with a gas atoms or molecules. When interactions happen, a complexity appears in measuring the ion interactions' products, but the calculations are simpler for  the velocity distribution for the electrons in many gases, since the ratio between a gas atom or molecule mass to the electron mass is very small. Since Producing electrons is simpler than producing ions in a gas,  many interactions are responsible for producing electrons, such as thermionic emission, photoemission, or radioactive decay. On the other hand,  creating an ion requires electron bombardment, photo-ionization or an electric discharge which requires more sophisticated conditions for the experiment and they are not as sensitive as the electrons for the the non-uniformity of the electric field, electric potential and magnetic field. Finally, the existence of the impurities is always a concern; the ions lose most of their energy in the molecular level, but the electron energy loss  within the atomic level in a pure gas, as a result, the ionic velocity distribution is not affected by the existence of these impurities except for some cases related to a highly accurate ionic studies in gases.
  
−
<math> D = 4 \pi \int_0^{\infty} \frac{c^2}{3\nu} f_0 c^2 dc </math>
 
  
−
<math>\nu</math> represents "effective collision frequency for the momentum transfer"<ref name="Huxley"/>,
+
==Electron Diffusion==
−
<math>f_0</math> is the is independent on '''r''' for a uniform stream that elastic collisions. In this case,
 
−
<math>f_0</math> is a special form of  a general form represented by the following equation:
 
  
−
<math> f_0 = A \exp{\int_0^c \frac{c dc }{V^2 + \bar{C^2}} }</math>
+
[[Diffusion]]
  
−
As a result substituting the main formula in the scalar form of Maxwell Boltzmann  , in the absence of the magnetic field ( vanishes) and in a uniform electric field '''E''', we get the following formula:
+
==ion Diffusion==
  
−
<math> \frac{\partial{}}{\partial{t}}</math>''n'' -
+
[[Ion Diffusion]]
−
''D''  <math> ( \frac {\partial^2{} }{\partial{x^2} }</math> +
 
−
<math> \frac {\partial^2{}} {\partial{ y^2}}</math>) ''n'' -
 
−
<math> D_L  \frac {\partial^2{}} {\partial{z^2} } </math> ''n''
 
−
+ ''W''  <math>\nabla_r n</math> = 0
 
  
−
''D'' is not isotropic as the e''E'' force is applied and  is  defined as in the equation above,  '''W''' is represented by the following:
 
  
−
<math> W = -\frac{4\pi}{3}(\frac{e}{m}) (\frac{E}{N}) \int_0^{\infty} \frac{c^2}{q_m (c)} \frac {df_0}{dc} dc </math>
+
== Multiplication ==
  
−
For electrons moving along the z-axis:
+
[[GEM pre-amplification]]
  
 +
==Decreasing the discharge in THGEM==
  
−
<math> - \frac{\partial{}}{\partial{t}}</math>''n'' +
+
GEm and THEGM preamplifiers are designed to be rebust, economical, and to get the maximum gain with the least discharge effect.  
−
''D''  <math> ( \frac {\partial^2{} }{\partial{x^2} }</math>''n'' +
 
−
<math> \frac {\partial^2{}} {\partial{ y^2}}</math>''n'' )  +
 
−
<math> D_L  \frac {\partial^2{}} {\partial{z^2} } </math>
 
−
- ''W''  <math>\frac{\partial{ }}{\partial{z} }</math> ''n'' = 0
 
−
 
 
−
 
 
−
<math> W = -\frac{4\pi}{3}(\frac{e}{m}) (\frac{E}{N}) \int_0^{\infty} \frac{c^2}{q_m (c)} \frac {df_0}{dc} dc </math>
 
−
 
 
−
<math> \sigma_{coll} (c) = 4\pi n c^2 \nu_{el} (\frac {m}{M} c f_0 + \frac{\bar{C^2}}{3} \frac{\partial{f_0}}{\partial{c}}) </math>
 
−
 
 
−
<math> \sigma_E (c) = \frac{4\pi}{3}  c^2 \frac {eE}{m} n f_1 </math>
 
−
 
 
−
<math> \nu_{el} = Ncq_{el}(c) </math>
 
−
 
 
−
===Main differences between electrons and ions behavior in a gas <ref name="Mason">Mason, Edward A. and Earl W. MacDaniel. 1988. Transport Properties of Ions in Gases. John Wiley & Sons. </ref>===
 
−
 
 
−
Haitham, here is a chance to get help with writing from the help center. 
 
−
Take the paragraph below to them and learn how to correct it.
 
−
 
 
−
H: Sure, but I need to add and edit some more to complete the idea then I will go there.
 
−
 
 
−
 
−
 
 
−
The ratio between the mass of the electrons and the gas atoms is very small, so with a few eV work done by the electric field, the electrons will gain a high velocity compared to that of the ions when are accelerated under the same electric field.
 
−
 
 
−
The probability of low energy electrons to make an interaction is higher than that of the low energy ions, in addition to a supported accurate calculations for the electron drift velocity in the case of electrons. Electrons at low energy have the ability to produce vibrations and excitations  in the gas atoms or molecules measured within the lab frame, but the low energy ions have a very low cross sections for the most of the interactions with the gas atoms or molecules, and in case of of having interactions, a complexity is  in measuring the products of these interactions. Furthermore, the ratio between a gas atom or molecule mass to the electron mass is very small which simplifies the calculations for the velocity distribution for the electrons in many gases.
 
−
 
 
−
Producing electrons is simpler than producing ions in a gas. a number of interactions appear in the gas for producing electrons like thermionic emission, photoemission, or a radioactive decay, on the other hand,  creating an ion requires electron bombardment, photo-ionization or an electric discharge which require more sophisticated conditions for the experiment. For instance , the ions are not as sensitive as the electrons for the the non-uniformity of the electric field, electric potential and magnetic field.
 
−
 
 
−
The last difference might be a concern in case of the existence of the impurities. The electrons loses most of their energy in the molecular level compared to the electron energy loss  within the atomic level for a pure gas. On the other hand, the ionic velocity distribution is not affected by the existence of these impurities except for some cases related to a highly accurate ionic studies in gases.
 
−
 
 
−
=== Gas Quenching===
 
−
 
 
−
Rewrite the first two sentences so quenching is more clearly described.
 
−
 
 
−
Gas quenching is a non-ionizing process occurs when a gas molecules with large cross sections for excitation and vibration states decreases a charged particle energy to create any ionization when the charged particle passes through. Usually, the gas mixture ,contains the ionization event, consists mostly of gas atoms as a main source of electrons and the quenching gas, when the free electrons are scattered after the ionization, their energy is decreased by quenching so the number of secondary electrons becomes less, Consequently,  a higher voltage is required to get a gain from this mixture than a medium only has a non-quenching gas<ref name="Sharma"> A.Sharma,F. Sauli, first Townsend coefficients measurements for argon gas european organization for nuclear research  (1993)  </ref >.
 
−
 
 
−
Not only does the quenching process decreases the electron energy, but also decreases the positive ions energy (produced by ionization) when the ions collide with these gas molecules and emits a photon or more from these positive ions. These photons represent the energy loss in a form other than the ionization which is called argon escape peak in case of using Argon gas.
 
−
 
 
−
Gas quenching experimentally can be measured by evaluating Townsend first coefficients A,B for different gas mixtures. The following table represents the Townsend first coefficients' values for different ratio of Ar/CO2 gas mixtures<ref name="Sharma"/>:
 
−
 
 
−
 
 
−
{| border="1" cellpadding="4"
 
−
|-
 
−
|Percentage of CO2 || 3.7 || 22.8 || 87.2 || 100
 
−
|-
 
−
| A <math> cm^{-1}Torr^{-1} </math> || 5.04 || 221.1 || 158.3 || 145.1
 
−
|-
 
−
|B <math> Vcm^{-1}Torr^{-1} </math> || 90.82 || 207.6 || 291.8 || 318.2
 
−
|-
 
−
| <math> \frac{E}{p} \,\,\, Vcm^{-1}Torr^{-1} </math> || 16.2 || 21.6 || 32.9 || 36.4
 
−
|}
 
−
 
 
−
The electric field pressure ratio in the last row is the upper limit of the reduced electric field which Townsend's equation fits considering E as a uniform electric field.
 
−
 
 
−
==Townsend's Coefficients==
 
−
 
 
−
 
 
−
===Townsend's First Coefficient===
 
−
 
 
−
Townsend's first Coefficient is defined as "the number of produced by an electron per unit length in the direction of the electric field"<ref name="Kuffel"/>.
 
−
 
 
−
 
 
−
*Townsend started his investigations about discharge after fundamental studies  were known around 1899 about:
 
−
 
 
−
1- Conductivity  production by x-rays.
 
−
 
 
−
2- Diffusion coefficients, mobility of ions and ion-electron
 
−
recombinations.
 
−
 
 
−
* It was observed for an increment in  Electric filed E and pressure P beyond the saturation current value, at some critical value of E and p, the current increases rapidly which will lead to a breakdown of the gap in the form of a spark  <ref name="loeb"> L.B.Loeb, basics processes of gaseous electronics, University of California Press, 2nd edition, 1955. call number  QC711 .L67 1955a </ref>.
 
−
 
 
−
*Townsend studied the relationship between E/p as a function of x, where x is the separation distance between the plates. His study was based on the photoelectron emission from the cathode by ultraviolet light at high uniform electric field up to 30kV/cm and 1 atm pressure.
 
−
 
 
−
 
 
−
*He plotted different values for E/p, he found that the slope of the line is <math>\alpha</math> which is "the number of the new electrons created by  single electron in 1 cm path in the filed direction in a gas at appropriately high E/p" <ref name="loeb"/> . Townsend plotted <math> \frac{i}{i_0} </math> against the distance of separation x, he concluded the following equation
 
−
 
 
−
<math> ln (\frac{i}{i_o}) = \alpha x </math>
 
−
 
 
−
to calculate  <math>\alpha</math> (the slope)  for different values of E/p as shown in the figure:
 
−
 
 
−
 
 
−
[[Image:alpha_town1st_coff_1.png |thumb| Fig. relationship between <math>ln{i}/{i_o}</math> and the distance x for different values of E/p <ref name="loeb"/>]]
 
−
 
 
−
* Townsend studied  <math>\alpha</math> as a function of E/p for a given gas, he founded ,for different values of p, 
 
−
<math>\alpha</math> experimentally is different from expected value calculated, but the plots met in values when it represented the relationship between  <math>\alpha</math>/p as a function of E/p as shwon in the figure below.
 
−
 
 
−
[[Image:alpha_p_E_p_rations.png |thumb| Fig. shows alpha p ratio coincides with E p ratio <ref name="loeb"/>]]
 
−
 
 
−
 
 
−
*The relationship between <math>\alpha</math>/p and E/p is shown below.  However, the equation can not predict all the values of <math>\alpha</math>/p accurately for different values  of E/p, i.e having a single analytical function to fit the experimental results for a gas does not exist, because <math>\alpha</math>/p is dependent on the number of electrons produced  which changes as the average energy distribution of the ionizing electrons changes <ref name="loeb"/>.
 
−
 
 
−
<math> \frac {\alpha}{P}= Ae^{(\frac{-BP}{E})} </math>
 
−
 
 
−
;Theoretical evaluation of <math>\alpha/p</math> as a function of E/p
 
−
 
 
−
* The first attempt was done by Townsend when the experimental data were limited by the to the high E/p.
 
−
 
 
−
===Decreasing the discharge in THGEM===
 
−
 
 
−
 
 
−
THEGM preamplifier is designed to be rebust, economical, and to get the maximum gain with the least discharge effect.  
 
  
 
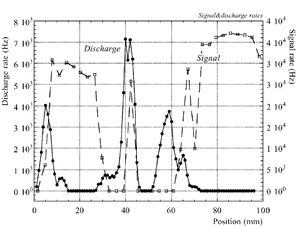
The discharge effect is when you experimentally start observing sparks coming from the detector. Whenever discharge becomes phenomenon to study then the probability of discharge is used. The probability of discharge is defined as the ratio between the observed frequency of the breakdown and source rate <ref name="bachmann"/>.The discharge rate and the source rate can be represented as function of position as shown in the figure.  
 
The discharge effect is when you experimentally start observing sparks coming from the detector. Whenever discharge becomes phenomenon to study then the probability of discharge is used. The probability of discharge is defined as the ratio between the observed frequency of the breakdown and source rate <ref name="bachmann"/>.The discharge rate and the source rate can be represented as function of position as shown in the figure.  
Line 329: Line 103:
 
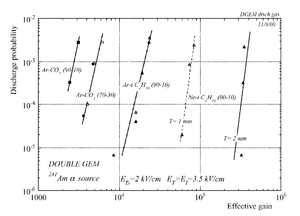
[[Image:Discharge_probability_gain_doubleGEM_bachmann.png |thumb| Fig. Discharge probability as function of gain for double GEM detector <ref name="bachmann"/>]]
 
[[Image:Discharge_probability_gain_doubleGEM_bachmann.png |thumb| Fig. Discharge probability as function of gain for double GEM detector <ref name="bachmann"/>]]
  
−
=Discharge in THGEM=
 
  
−
GEM and THGEM have similarities in factors that increases discharge in radiation harsh environment. Being  charge preamplifiers requires a high voltage provided by a voltage divider network which does not have resistors of order of hundred Mohm (then terminated by 50 ohm resistor oscilloscope). Setting the power supply to the maximum current limit causes a discharge,indeed high network resistors up to hundreds of Mohm , and connected to 50ohm terminated oscilloscope, were abandoned. The best difference in voltage for triple GEM is to have the 10% more that the second GEM and 10% less for the third GEM.
+
Experimetally, GEM and THGEM have similarities in factors that increases discharge in radiation harsh environment. Being  charge preamplifiers requires a high voltage provided by a voltage divider network which does not have resistors of order of hundred Mohm. Setting the power supply to the maximum current limit causes a discharge,indeed high network resistors up to hundreds of Mohm may limit the effect fo the returning current which will casue less discharge in the GEM or THGEM. Generally, the HV-circuit divides the voltage for triple GEM based detector in away that the voltage difference between the top and bottom of of the first preamplifer is 10% more than the second, and the second preamplifer is 10% more in voltagethan the third one to avoid the discharge effect throught the detector operaion.
 +
 
 +
The discharge probability is independent on gap voltage between two successive preamplifiers but adding 50 pF capacitor "lower the threshold considerably to the charge propagation". The charge propagation relies on the capacitance of GEM. Having the GEM with independently powered sectors reduces "the probability of energetic discharge propagation to the readout plate.
 +
 
 +
In some gases, The highest gain value ,in presence of heavily ionizing radiation, is affected by the gap between the THGEM cards due to the photon feedback mechanics.<ref name="Bachmann"> Nucl. Inst. and meth. 479 (2002) 294-308 </ref>.
  
−
The discharge probability is independent on gap voltage between two successive THGEM but adding 50 pF capacitor "lower the threshold considerably to the charge propagation".
 
  
−
The charge propagation relies on the capacitance of THGEM. Having the THGEM with independently powered sectors reduces "the probability of energetic discharge propagation to the readout plate.
 
  
−
In some gases, The highest gain value ,in presence of heavily ionizing radiation, is affected by the gap between the THGEM cards due to the photon feedback mechanics.<ref name="Bachmann"> Nucl. Inst. and meth. 479 (2002) 294-308 </ref>.
 
  
 
Photon feedback: emission and re-absorption of the photons in the gas or in the metal's surface.
 
Photon feedback: emission and re-absorption of the photons in the gas or in the metal's surface.
Line 387: Line 161:
  
 
<references/>
 
<references/>
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
GO BACK [https://wiki.iac.isu.edu/index.php/Performance_of_THGEM_as_a_Neutron_Detector]

Latest revision as of 14:54, 23 June 2015

Related Physical Concepts

The gaseous medium inside a detector's chamber contains different physical processes as a particle arrives the gas. When the desired particles penetrate the gaseous medium, they directly or indirectly (neutron fission) ionize the gas. If the event happened in the active detection area of the detector, a drift electric field guides the primary and secondary electrons toward the GEM preamplifiers, These preamplifiers are placed to have a separation distance within a limit to not lose the electrons by keeping their diffusion to be a reason for their multiplication . An electron avalanches appear and the negative voltage directs them toward the read out plate which collects the electrons to show them as negative pulses on the oscilloscope's screen. Electron recombination, deattachment and capture take place in every stage in the electron trip before they reach the readout plate. The output signal is important to measure the detector's performance by determining its efficiency, dead time, gain, spatial resolution and robustness.Theoretically, the detector output can be evaluated by solving Boltzmann equation that considers the effect of each physical process occurred.


Ionization

Ionization is the liberation of an electron from the medium's atoms or its molecules. The minimum amount of energy required to liberate the electron is referred to as the ionization energy. When the ionizing particle gets in the medium, it deposits its energy to scatter free electrons which they get their kinetic energy after losing part of their energy in releasing from the atom confinement, and after passing through electron-electron collisions. For instance, charged particles like fission fragments ionizes the medium and scatter free electrons, the kinetic energy depends on the fission fragment's energy gained after ionization and the number of collisions the electron passes through.

The ionization is a stochastic process, it depends on the ionization cross section that is determined by the ionizing particle energy, and mass(heavy or light in case of fission fragments). However, the amount of energy needed to have an ionization event on average is the same, regardless of the incident particle type or energy as shown in the following table for argon gas.<ref name="Veenhof"> R. Veenhof, Internal Note/TPC, ALICE-INT-2003-29 version 1.0, 2003</ref>


Type of particle and its energy 9 keV x-rays 10 keV electrons 40 keV electrons x-rays Ar-37(K-capture)(5-25 keV) + beta alpha 7.68 MeV 340 MeV protons
Energy per ion-electron pair (eV) 27.9 [math]\pm[/math] 1.5 27.3 25.4 27.0 [math]\pm[/math]0.5 26.25 25.5

Ionization in fission chambers

Ionization by a fission fragment is not the only source for free electrons and it is not the only ionization process in fission chamber. Fission chambers usually contain neutoron fissinable materials, they are heavy radioisotopes that decay and emit more than one type of the ionizing radiation or by their daughters after decay. For instance, when the fission chamber contains U-233, free electrons are detected because of escaping fission fragments, alpha particles, beta particles, or gamma rays. More specific details about U-233 decay products is shown by the following tables:

nuclide Energy Minimum Energy Maximum (keV)
U-233 25 1,119
Ra-225 40 40
Ac-225 10.5 758.9
Fr-221 96.8 410.7
At-217 140 593.1
Bi-213 323.81 1,119.4



Nuclides energy (MeV) half life
[math]Ra^{225} \rightarrow Ac^{225}[/math] 0.357 14d.
[math]Bi^{213} \rightarrow Po^{213}[/math] 1.426 46min.
[math]Tl^{209} \rightarrow Pb^{209}[/math] 1.981 2.2 min.
[math]Pb^{209} \rightarrow Bi^{209}[/math] 0.644 3.25h
[math]Bi^{209}[/math] 1.893 stable

To count the free electrons produced by the fission fragments demands some modifications in the detector design which mentioned in details in detector construction section .

They are other physical processes occur in the medium which are related to the gas mixture properties such as: photoionization, thermal ionization, deionization by attachment (negative ion formation) , photoelectric emission, electron emission by excited atoms or positive ion,penning ,and field emission <ref name="Kuffel"/>. The previous processes may share in decreasing or increasing the number of free electrons in the medium, so evaluating the number of free electrons before preamplification becomes sophisticated without a computer simulation.


Garfield simulates the ionization in the gas mixture cosidering all the former physical processes, it has the ability to simulate the electrons multiplication by GEM preaplifiers, it accepts external solutions for the electric field by other software packages like ANSYS, and it has more than one package such as Magboltz, HEED, and Imonte 4.5 that can be used for more precise simulations <ref name="Veenhof"/>.

Diffusion

Main differences between electrons and ions behavior in a gas <ref name="Mason">Mason, Edward A. and Earl W. MacDaniel. 1988. Transport Properties of Ions in Gases. John Wiley & Sons. QC717.5 I6 M37 </ref>

Studying diffusion and mobility of charged particles in a gas is classified in to two main groups, ion and electron diffusion and mobility. They are conceptually similar, but they have many differences. First, The ratio between the mass of the electrons and the gas atoms is very small, so with a few eV work done by the electric field, the electrons will gain a high velocity compared to that of the ions that are accelerated under the same electric field. Also, the probability of low energy electrons to make an interaction is higher than that of the low energy ions, the electron interactions are a supported with accurate calculations for the electron drift velocity. Electrons at low energy have the ability to produce vibrations and excitations in the gas atoms or molecules which are measured within the lab frame, but low energy ions have very low cross sections for most of the interactions with a gas atoms or molecules. When interactions happen, a complexity appears in measuring the ion interactions' products, but the calculations are simpler for the velocity distribution for the electrons in many gases, since the ratio between a gas atom or molecule mass to the electron mass is very small. Since Producing electrons is simpler than producing ions in a gas, many interactions are responsible for producing electrons, such as thermionic emission, photoemission, or radioactive decay. On the other hand, creating an ion requires electron bombardment, photo-ionization or an electric discharge which requires more sophisticated conditions for the experiment and they are not as sensitive as the electrons for the the non-uniformity of the electric field, electric potential and magnetic field. Finally, the existence of the impurities is always a concern; the ions lose most of their energy in the molecular level, but the electron energy loss within the atomic level in a pure gas, as a result, the ionic velocity distribution is not affected by the existence of these impurities except for some cases related to a highly accurate ionic studies in gases.


Electron Diffusion

Diffusion

ion Diffusion

Ion Diffusion


Multiplication

GEM pre-amplification

Decreasing the discharge in THGEM

GEm and THEGM preamplifiers are designed to be rebust, economical, and to get the maximum gain with the least discharge effect.

The discharge effect is when you experimentally start observing sparks coming from the detector. Whenever discharge becomes phenomenon to study then the probability of discharge is used. The probability of discharge is defined as the ratio between the observed frequency of the breakdown and source rate <ref name="bachmann"/>.The discharge rate and the source rate can be represented as function of position as shown in the figure.


Fig. Discharge rate and the detected source rate can be represented as function of position <ref name="bachmann"/>

Producing these sparks refers to many reasons,it is obviously observed when a highly ionizing ion passes through the gaseous chamber and produces enough free electrons to break down the rigidity of surrounding gas by having an avalanche size exceeds Raether limit ( [math] 10^7[/math] electron-ion pairs) when separating the electrodes vertically with small a distance <ref name="bachmann"> Bachmann et al NIM A 479 (2002) 294-308 </ref > .

Temperature, humidity, and gas flow externally affect the probability of the transition from the proportional multiplication to a discharge at a given potential, the effect clearly appears in absence of the amplification internal effects as the design quality and the history of the electrodes <ref name="bachmann"/>.

In case of heavily ionizing ions like alpha particles, an increase in gain causes the probability of discharge to increase, but the increment in the probability of discharge can be decreased by choosing an appropriate gap between the THGEM cards <ref name="bachmann"/>. As a result, achieving a maximum gain for an incident particle on a chamber with a specific gas mixture ,under a voltage applied on the THGEM cards, requires an appropriate distance that increases with increment of the ionization rate, i.e an alpha particle requires a bigger gap between the THGEM cards than that of a gamma ray to avoid the discharge effect.(can be experimentally proven).


Fig. Discharge probability as function of gain for double GEM detector <ref name="bachmann"/>


Experimetally, GEM and THGEM have similarities in factors that increases discharge in radiation harsh environment. Being charge preamplifiers requires a high voltage provided by a voltage divider network which does not have resistors of order of hundred Mohm. Setting the power supply to the maximum current limit causes a discharge,indeed high network resistors up to hundreds of Mohm may limit the effect fo the returning current which will casue less discharge in the GEM or THGEM. Generally, the HV-circuit divides the voltage for triple GEM based detector in away that the voltage difference between the top and bottom of of the first preamplifer is 10% more than the second, and the second preamplifer is 10% more in voltagethan the third one to avoid the discharge effect throught the detector operaion.

The discharge probability is independent on gap voltage between two successive preamplifiers but adding 50 pF capacitor "lower the threshold considerably to the charge propagation". The charge propagation relies on the capacitance of GEM. Having the GEM with independently powered sectors reduces "the probability of energetic discharge propagation to the readout plate.

In some gases, The highest gain value ,in presence of heavily ionizing radiation, is affected by the gap between the THGEM cards due to the photon feedback mechanics.<ref name="Bachmann"> Nucl. Inst. and meth. 479 (2002) 294-308 </ref>.



Photon feedback: emission and re-absorption of the photons in the gas or in the metal's surface.

Reminders

Basic definitions<ref name="Petrovic"> Z Lj Petrovi´c, S Dujko J. Phys. D
Appl. Phys. 42 (2009) 194002 </ref>

1- Enhanced electron conductivity: effect shows an increase in the electron drift velocity in a system encounters inelastic collisions with small probability for drift velocity in all directions when it is directed by an electric field.

2- Negative differential conductivity: An effect is observed when the increase in electric field density ratio leads to a decrease in the drift velocity. "NDC was found to be favoured by increasing momentum transfer and decreasing inelastic cross sections and the balance of different processes affecting it can be put into a condition which is relatively accurate". it observed in argon mixtures.







Physical parameter and its eefect on the detector properties
physical parameter Effect on the detector properties <ref name="Veenhof"/>
Electron drift velocity Dead time
Electron transverse diffusion Spatial resolution (momentum resolution), transverse resolution should match the response function (signal width)
Townsend Coefficient Gain which improves the resolution
Attachment Coefficient Losing the information about an ionization, affects the position information and dE/dx identification
Gas breakdown Discharge at that voltage
Ion mobility Determine the rate of collecting the electrons (if the space charge is eliminated), the signal duration in the readout plate
Ionization rate Affect the spatial resolution, dE/dx identification

Boundary Element Method (BEM)

Boundary Element Method is used to solve Laplace or Poisson Equation, a function u(x,y,z) is solved on the domain boundary and the function partial derivatives are evaluated by integrating on the number of elements on the boundary.<ref name="Kuffel"> Kuffel, W. S. Zaengl, J. Kuffel, High voltage engineering: fundamentals, Biddle Ltd, 2nd edition, 2000 </ref>.


<references/>











GO BACK [1]

Retrieved from "https://wiki.iac.isu.edu/index.php?title=Gaseous_Medium_Physical_Concepts&oldid=101204"