GEM pre-amplification

Electron Multiplication

Generally, most of gases are neutral in low electric field, under standard room temperature and pressure. Gases' atoms and molecules tend to stay in the lowest energy level, so the number of collisions among the atoms and molecules become relatively low at standard conditions for temperature and pressure in an area of a low electric field. Those collisions will cause a low ionization in the medium down to [math] 10^{-16}-10^{-17} [/math] A/cm^2 (including the ionization by the cosmic rays). Changing any of these factors may increase the ionization of a gas. This section will discuss the principles that describe increasing the electric field on the number of free electrons in a gas.

Townsend's First Coefficient

Townsend's first Coefficient is defined as "the number of produced by an electron per unit length in the direction of the electric field"<ref name="Kuffel"/>.

Historically, Townsend started his investigations about discharge after the fundamental studies were known in around 1899, these studies were about: Conductivity production by x-rays, diffusion coefficients, mobility of ions, ion-electron recombinations. It was observed for an increment in electric field E and pressure P beyond the saturation current value, at some critical value of E and p, the current increases rapidly and lead to a breakdown of the gap in the form of a spark. <ref name="loeb"> L.B.Loeb, basics processes of gaseous electronics, University of California Press, 2nd edition, 1955. call number QC711 .L67 1955a </ref>. So, Townsend studied the relationship between E/p as a function of x, where x is the separation distance between the plates. His study was based on the photoelectron emission from the cathode by ultraviolet light at high uniform electric field up to 30kV/cm and 1 atm pressure. He plotted different values for E/p, he found that the slope of the line is [math]\alpha[/math] which is "the number of the new electrons created by a single electron in 1 cm path in the filed direction in a gas at appropriately high E/p" <ref name="loeb"/> . Townsend plotted [math] \frac{i}{i_0} [/math] against the distance of separation x, he concluded the following equation :

[math] ln (\frac{i}{i_o}) = \alpha x [/math]

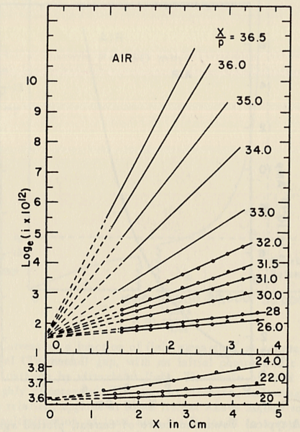
to calculate [math]\alpha[/math] (the slope) for different values of E/p as shown in the figure:

Fig. relationship between [math]ln{i}/{i_o}[/math] and the distance x for different values of E/p <ref name="loeb"/>

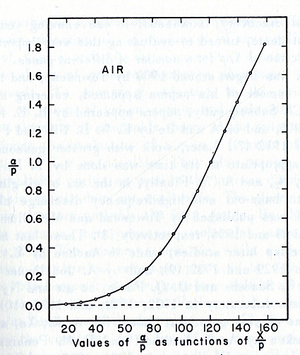
Townsend studied [math]\alpha[/math] as a function of E/p for a given gas, he founded for different values of p, [math]\alpha[/math] is experimentally different from expected calculated value, but the plots met in values when it represented the relationship between [math]\alpha[/math]/p as a function of E/p as shown in the figure below.

Fig. shows alpha p ratio coincides with E p ratio <ref name="loeb"/>

The relationship between [math]\alpha[/math]/p and E/p is shown below, the equation can not predict all the values of [math]\alpha[/math]/p accurately for different values of E/p, i.e having a single analytical function to fit the experimental results for a gas does not exist, because [math]\alpha[/math]/p is dependent on the number of electrons produced, the electrons number changes with changing the average energy distribution of the ionizing electrons <ref name="loeb"/>.

[math] \frac {\alpha}{P}= Ae^{(\frac{-BP}{E})} [/math]

One of the ways to mathematically evaluate [math]\alpha/p[/math] as a function of E/p is by the kinetic theory. The kinetic thory describes the gas atoms and molecules' energy and their collision rates depending on the mean free path of ionization. it defines the average mean free path by:

[math] \bar{\lambda} = \frac{kT}{p \sigma_i} [/math]

where [math] \sigma_i [/math] is the ionization cross section.

[math] \alpha = -\frac{f'(x)}{dx} = 1/\bar{\lambda} e^{\lambda_i/\bar{\lambda}} \,\,\, f'(x) = e^{-x/\bar{\lambda}} [/math]

where x is the distance traveled by the electron. Substituting the value of [math] \lambda[/math]

[math] \frac{\alpha}{p} = \frac{\sigma_i}{kT} e^{-\sigma_i/kT (V_i/(E/p))} = A e^{-B/(E/T)} [/math]

where ;

[math] A = \frac{\sigma_i}{kT} \,\,\,\, and \,\,\, B = \frac {\sigma_i Vi}{kT} [/math]

The values for A and B do not always agree with the exprimetal values<Kuffel/>. Since it is assumed that if the electron energy is greaterthan [math]eV_i [/math], it will lead to ionization, however, the ionization probability does not always increase with increasing the the electron energy. Also the mean free path is defined as independent on the electron energy which is not always true.

Gas Quenching

Rewrite the first two sentences so quenching is more clearly described.

Gas quenching is a non-ionizing process occurs when a gas molecules with large cross sections for excitation and vibration states decreases a charged particle energy to create any ionization when the charged particle passes through. Usually, the gas mixture ,contains the ionization event, consists mostly of gas atoms as a main source of electrons and the quenching gas, when the free electrons are scattered after the ionization, their energy is decreased by quenching so the number of secondary electrons becomes less, Consequently, a higher voltage is required to get a gain from this mixture than a medium only has a non-quenching gas<ref name="Sharma"> A.Sharma,F. Sauli, first Townsend coefficients measurements for argon gas european organization for nuclear research (1993) </ref >.

Not only does the quenching process decreases the electron energy, but also decreases the positive ions energy (produced by ionization) when the ions collide with these gas molecules and emits a photon or more from these positive ions. These photons represent the energy loss in a form other than the ionization which is called argon escape peak in case of using Argon gas.

Gas quenching experimentally can be measured by evaluating Townsend first coefficients A,B for different gas mixtures. The following table represents the Townsend first coefficients' values for different ratio of Ar/CO2 gas mixtures<ref name="Sharma"/>:

Percentage of CO2	3.7	22.8	87.2	100
A [math] cm^{-1}Torr^{-1} [/math]	5.04	221.1	158.3	145.1
B [math] Vcm^{-1}Torr^{-1} [/math]	90.82	207.6	291.8	318.2
[math] \frac{E}{p} \,\,\, Vcm^{-1}Torr^{-1} [/math]	16.2	21.6	32.9	36.4

The electric field pressure ratio in the last row is the upper limit of the reduced electric field which Townsend's equation fits considering E as a uniform electric field.

Why 90/10 Ar/CO2 Mixture and why Garfield <ref name="Veenhof"/>

why Garfield

<references/>