Difference between revisions of "EG1 Teleconferences DeltaDoverD"
| Line 117: | Line 117: | ||
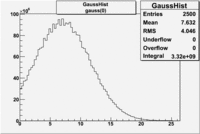
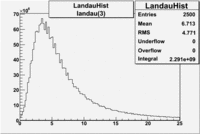
<math> = \frac {Integral(gauss(0))}{Integral(gauss(0) + landau(3) + gauss(6))} =</math><br> | <math> = \frac {Integral(gauss(0))}{Integral(gauss(0) + landau(3) + gauss(6))} =</math><br> | ||
<math> = \frac{3.32 \times 10^9}{ 3.32 \times 10^9 + 2.291 \times 10^9 + 3.8 \times 10^8} = </math> <br> | <math> = \frac{3.32 \times 10^9}{ 3.32 \times 10^9 + 2.291 \times 10^9 + 3.8 \times 10^8} = </math> <br> | ||
| − | <math> = | + | <math> = ? % </math><br> |
;2.) Electrons in the sample | ;2.) Electrons in the sample | ||
| Line 125: | Line 125: | ||
Electrons in the sample(all cuts) =<br> | Electrons in the sample(all cuts) =<br> | ||
<math> = \frac {Integral(gauss(0))}{Integral(gauss(0) + landau(3) + gauss(6))} =</math><br> | <math> = \frac {Integral(gauss(0))}{Integral(gauss(0) + landau(3) + gauss(6))} =</math><br> | ||
| − | <math> = \frac{ | + | <math> = \frac{ 3.269 \times 10^9}{ 3.269 \times 10^9 + 2.285 \times 10^9 + 3.571 \times 10^8} = </math> <br> |
<math> = ? % </math><br> | <math> = ? % </math><br> | ||
Revision as of 01:32, 12 February 2009
2/12/09
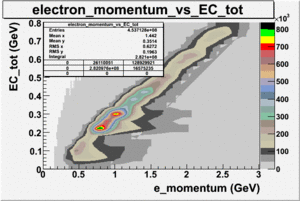
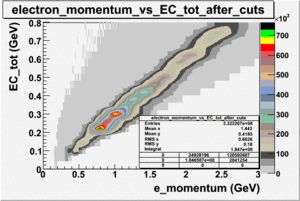
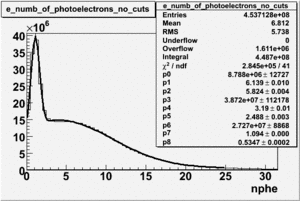
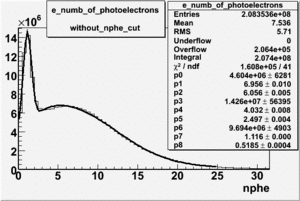
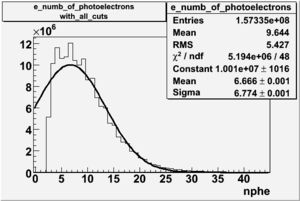
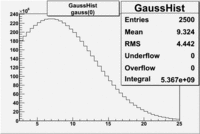
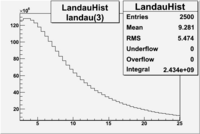
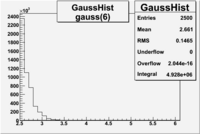
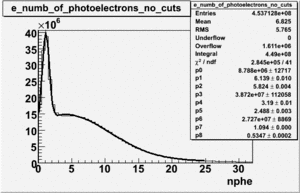
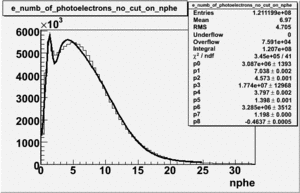
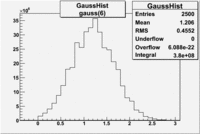
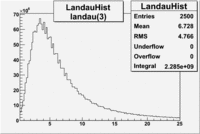
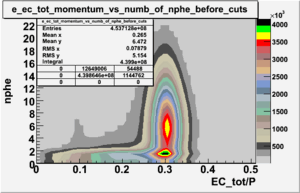
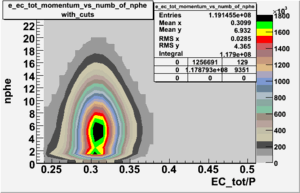
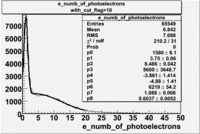
Cuts are applied on the electron candidates based on the ratio of the energy deposited by the electron candidate in the electron calorimeter to the particles momentum measured by track reconstruction using hits in the drift chamber. As reported at the last teleconference on 1/20/09, these cuts were taken from Media:Yelena_Prok_Measurement_of_The_Spin_structure_Function_of_The_Proton_in_The_Resonance_Region_Thesis.pdf and applied to the 5 GeV data sample. The number of photoelectrons measured by the cherenkov detector is shown below. The goal is to estimated the number of pions which contaminate the electron candidate sample. This is done by fitting the photoelectron distribution to 2 gaussian distributions and a Landau distribution. Integrals of the fits over the region of interest are used determine the pion contamination to the electron candidates.
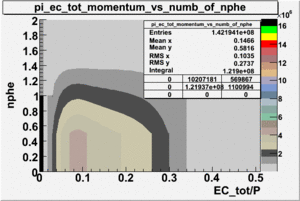
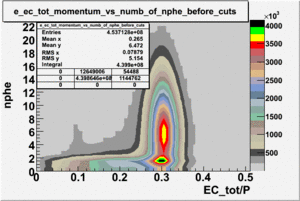
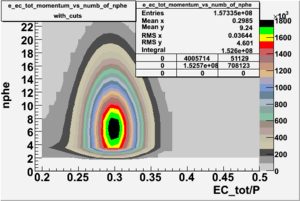
Number of photoelectrons and EC_tot/P vs nphe for Pions and Electrons when e_momentum < 3 GeV
| Momentum (GeV) | /P | /P | Cherenkov cut |
| e_momentum<3 | >0.2 | >0.08 | nphe>2.5 |
| Distributions | amplitude | mean | width | amplitude | mean | width |
|---|---|---|---|---|---|---|
| without cuts | with cuts(, , e_momentum<3 GeV) | |||||
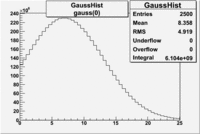
| gauss(0) | p0=8.788e+06 +\-12727 | p1=6.139 +\-0.010 | p2=5.824 +\-0.004 | p0=4.604e+06 +\-6281 | p1=6.956 +\-0.010 | p2=6.056 +\-0.005 |
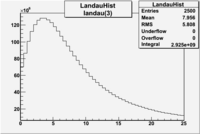
| landau(3) | p3=3.872e+07 +\-112178 | p4=3.19 +\-0.01 | p5=2.488 +\-0.003 | p3=1.426e+07 +\-56395 | p4=4.032 +\-0.008 | p5=2.497 +\-0.004 |
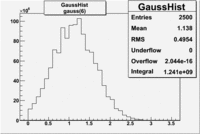
| gauss(6) | p6=2.727e+07 +\-8868 | p7=1.094 +\-0.000 | p8= 0.5347 +\-0.0002 | p6=9.694e+06 +\-4903 | p7=1.116 +\-0.000 | p8= 0.5185 +\-0.0004 |
- 1.) Electrons in the sample
Electrons in the sample(using all cuts except nphe>2.5) =
- 2.) Electrons in the sample
Electrons in the sample(using all cuts except nphe>2.5) =
- For Pions
In this case, Josh's pion cut code was used. The number of entries decreased by ~
- For Electrons
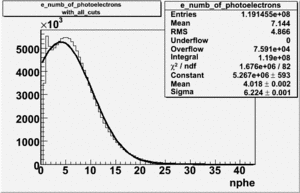
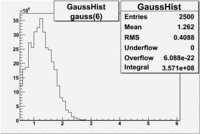
In order to remove the peak around ~ 1.5 PE and some high energy pions which have enough energy to cause the Cherenkov radiation the cut on nphe was applied. The number of entries after applying the following cuts - , e_momentum < 3 GeV and nphe > 2.5 decreased by 65.31 %.
Number of photoelectrons and EC_tot/P vs nphe for Pions and Electrons when e_momentum > 3 GeV
| Momentum (GeV) | /P | /P | Cherenkov cut |
| e_momentum<3 | >0.24 | >0.06 | nphe>0.5 |
| Distributions | amplitude | mean | width | amplitude | mean | width |
|---|---|---|---|---|---|---|
| without cuts | with cuts(, , e_momentum>3 GeV) | |||||
| gauss(0) | p0=?e+06 +\- | p1=6.139 +\- | p2=5.824 +\- | p0=3.087e+06 +\-1393 | p1=7.038 +\-0.002 | p2=4.573 +\-0.001 |
| landau(3) | p3=3.872e+07 +\- | p4=3.19 +\- | p5=2.488 +\- | p3=1.774e+07 +\-12968 | p4=3.797 +\-0.002 | p5=1.398 +\-0.001 |
| gauss(6) | p6=2.727e+07 +\- | p7=1.094 +\- | p8= 0.5347 +\- | p6=3.285e+06 +\-3512 | p7=1.198 +\-0.000 | p8= -0.4637 +\-0.0005 |
- 1.) Electrons in the sample
Electrons in the sample(using all cuts except nphe>2.5) =
- 2.) Electrons in the sample
Electrons in the sample(all cuts) =
- For Pions
In this case, Josh's pion cut code was used. The number of entries decreased by ~
- For Electrons
In order to remove the peak around ~ 1.5 PE and some high energy pions which have enough energy to cause the Cherenkov radiation the cut on nphe was applied. The number of entries after applying the following cuts - , e_momentum < 3 GeV and nphe > 2.5 decreased by 65.31 %.
1/29/09
We are interested in measuring the semi-inclusive pion asymmetry for both proton and deuteron targets using the 5-6 GeV EG1b data set. Our goal will be to investigate fragmentation and establish a procedure for extracting within the CLAS 12 GeV program. We begin the analysis using the EG1 DSTs created from "cooked" data files. Our first goal is evaluate the cuts used by others to improved the identification of scattered electrons in the data sample.
Cherenkov signal
Cherenkov PE Calculation
As shown in the wiki section, Particle_Identification#Cherenkov,
the expected number of photoelectrons produced by electrons traversing the CLAS cherenkov detector would be
if you assume a of 1 for the detected electrons in our data sample.
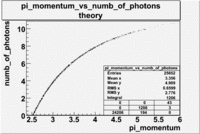
The expected number of photoelectrons in the CLAS cherenkov detector for reconstructed pion energies in the EG1 data set is shown in the graph below.
Our theoretical expectation, based on the description of the CLAS cherenkov detector suggests, that pions can generate up to about 10 photoelectrons compared with the 13 photoelectrons that can be generated by electrons. While the cherenkov detector can distinguish a 4 photoelectron signal generated by pions of momentum 3 GeV or less from the 10 photoelectrons generated by the typical detected electron, high momentum pions would generate photoelectron signals which are comparable to the photoelectrons generated by an electron.
Measured CLAS Cherenkov signal
Electrons
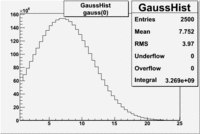
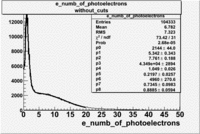
The cherenkov signal measured in CLAS for particles identified as electrons by the tracking algorithm is shown below. There are two distributions present. One distribution is centered around 0.7 PEs and the second distribution is at 5.3 PEs when two gaussians and a Landau distribution are combined and fit to the spectrum.
- PE Fit equation (Osipenko's CLAS Note 2004-20 File:CLAS Note-2004-020.pdf)
As we will show below, the first peak is due to the misidentification of a negative pion as an electron.
Reconstruction of an electrons trajectory through the CLAS drift chambers can be done using either 5 or 6 super layers. Do tracks reconstructed using 5 superlayers generate cherenkov signals which differ from tracks reconstructed using all 6 DC superlayers? The track reconstruction algorithm records the number of superlayers used for the track reconstructions. This number is recorder in the EG1 DST files within the "flag" variable. If the "flag" variable in the DST is larger than 10, then 6 superlayers were used for the track reconstruction. The cherenkov spectrum below is observed for particles identified as electrons in the EG1 data in which 6 superlayers have been used to determine their trajectory.
The table below compares the cherekov spectrum fit values for particles identified as electrons with and without the 6 superlayer requirement. If 6 superlayers are required for the electron reconstruction, the high PE gaussian distribution mean changes from 5.3 PEs to 3.8 PEs and is not not consistent within 2 standard deviations of the fit errors. The LOW PE gaussian distribution, the suspected pion contamination, mean changes from 0.7 to 1.0 PEs.
The cuts decreases the number of entries by 37.17 %. It is believed that the Gaussian distribution centered around 1 PE is due to high energy pions(>2.5GeV). Neither of these distributions is consistent with the theoretical predictions made above suggesting that there are some light collection inefficiencies within the cherenkov detector.
Table: Cherenkov fit values
| Distributions | amplitude | mean | width | amplitude | mean | width |
|---|---|---|---|---|---|---|
| without cuts | with cut(flag>10) | |||||
| gauss(0) | p0=2144+/-44.0 | p1=5.342+/-0.343 | p2=7.761+/-0.188 | p0=1580+/-8.1 | p1=3.75+/-0.06 | p2=8.486+/-0.042 |
| landau(3) | p3=4.349e+04+/-2894 | p4=1.049+/-0.026 | p5=0.2197+/-0.0257 | p3=8600+/-3648.7 | p4=-3.861+/-1.414 | p5=-4.88+/-1.41 |
| gauss(6) | p6=4960+/-270.6 | p7=0.7345+/-0.0983 | p8=0.8885+/-0.0594 | p6=6219+/-54.2 | p7=1.088+/-0.006 | p8=0.6037+/-0.0052 |
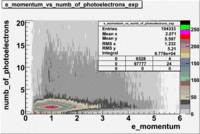
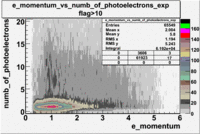
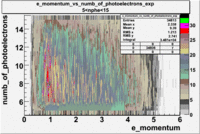
The plots below show the event population intensity as a function of the electron candidates momentum measured by tracking and the number of photoelectrons observed in the cherenkov detector
| Experiment | B>0 | without cuts | flag>10 | 5<nphe<15 | 5<nphe<15 and flag>10 |
|---|---|---|---|---|---|
|
|
|
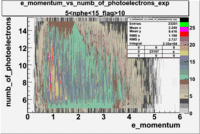
|
Pions()
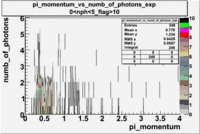
- _Momentum_vs_Number_of_Photons
The histograms presented below show the event population intensity for the pion momentum and the number of photoelectrons generated by the pions. One can see that after applying cuts on NPhE and flag the mean value is around 1.
| Experiment | B>0 | without cuts | e_flag>10 | 0<e_nphe<5 | 0<nphe<5 and e_flag>10 |
|---|---|---|---|---|---|
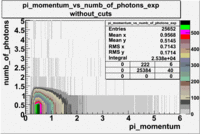
|
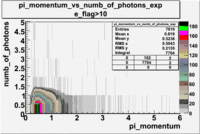
|
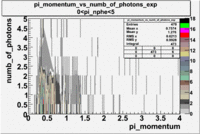
|
|
Electron-pion contamination
Osipenko's CLAS Note 2004-20 File:CLAS Note-2004-020.pdf
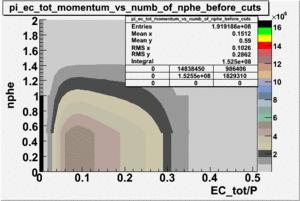
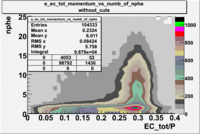
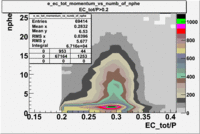
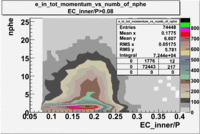
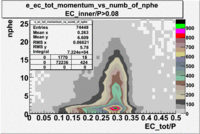
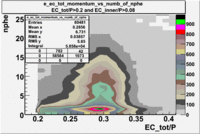
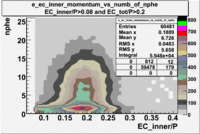
- EC_tot/P_vs_Number_of_Photoelectrons and EC_inner/P_vs_Number_of_Photoelectrons
Two types of cuts were applied on the distributions below, one on the energy deposited to the inner calorimeter and another one on the total energy absorbed by the calorimeter , to improve the electron particle identification. In this case we used the DST file dst27095_05, the beam energy is 5.735 GeV and target NH3.
| without cut | _vs_nphe() | _vs_nphe () | _vs_nphe() |
|---|---|---|---|
|
|
|
|
| _vs_nphe() | _vs_nphe( and ) | _vs_nphe ( and ) |
|---|---|---|

|
|
|