TF SPIM Intro

Introduction

Experimentalists use simulations to predict the sources of background which will interfere with the signal they plan on measuring. An important aspect of this process is to understand how signals are produced in your measurement device. Devices share the common problem of isolating a signal produced in the device from the noise that is present in the device.

Below is a description of how signals are produced in bulk materials.

Particle Detection

A device detects a particle only after the particle transfers energy to the device.

Energy intrinsic to a device depends on the material used in a device

Consider a device made of some material with an average atomic number ([math]Z[/math]) at some temperature ([math]T[/math]). The material's atoms are in constant thermal motion (unless you can manage to have T = zero degrees Klevin).

Statistical Thermodynamics tells us that the canonical energy distribution of the atoms is given by the Maxwell-Boltzmann statistics such that

[math]P(E) = \frac{1}{kT} e^{-\frac{E}{kT}}[/math]

[math]P(E)[/math] represents the probability of any atom in the system having an energy [math]E[/math] where

[math]k= 1.38 \times 10^{-23} \frac{J}{mole \cdot K}[/math]

Note: You may be more familiar with the Maxwell-Boltzmann distribution in the form

[math]N(\nu) = 4 \pi N \left ( \frac{m}{2\pi k T} \right ) ^{3/2} v^2 e^{-mv^2/2kT}[/math]

where [math]N(v) \Delta v[/math] would represent the molecules in the gas sample with speeds between [math]v[/math] and [math]v + \Delta v[/math]

Example 1: P(E=5 eV)

What is the probability that an atom in a 12.011 gram block of carbon would have an energy of 5 eV?

First lets check that the probability distribution is Normalized; ie: does [math]\int_0^{\infty} P(E) dE =1[/math]?

[math]\int_0^{\infty} P(E) dE = \int_0^{\infty} \frac{1}{kT} e^{-\frac{E}{kT}} dE = \frac{1}{kT} \frac{1}{\frac{1}{-kT}} e^{-\frac{E}{kT}} \mid_0^{\infty} = - [e^{-\infty} - e^0]= 1[/math]

Physically, [math]P(E=5eV)[/math] is calculated by integrating P(E) over some energy interval ( ie:[math] N(v) dv[/math]). I will arbitrarily choose 4.9 eV to 5.1 eV as a starting point.

[math]\int_{4.9 eV}^{5.1 eV} P(E) dE = - [e^{-5.1 eV/kT} - e^{4.9 eV/kT}][/math]

[math]k= \left (1.38 \times 10^{-23} \frac{J}{mole \cdot K} \right ) = \left (1.38 \times 10^{-23} \frac{J}{mole \cdot K} \right ) \left (6.42 \times 10^{18} \frac{eV}{J} \right )= 8.614 \times 10^{-5} \frac {eV}{mole \cdot K}[/math]

assuming a room temperature of [math]T=300 K[/math]

then[math]kT = 0.0258 \frac{eV}{mole}[/math]

and

[math]\int_{4.9 eV}^{5.1 eV} P(E) dE = - [e^{-5.1/0.0258} - e^{4.9/0.0258}] = 4.48 \times 10^{-83} - 1.9 \times 10^{-86} \approx 4.48 \times 10^{-83}[/math]

or in other words the probability may be approximated by just using the distribution function alone

[math]P(E=5eV) = e^{-5/0.0258} \approx 10^{-85}[/math]

This approximation breaks down as [math]E \rightarrow 0.0258 eV[/math]

Since we have 12.011 grams of carbon and 1 mole of carbon = 12.011 g = [math]6 \times 10^{23} [/math]carbon atoms, we would not expect to see a 5 eV carbon atom in a sample size of [math]6 \times 10^{23} [/math] carbon atoms when the probability of observing such an atom is [math]\approx 10^{-85}[/math]. Note: The mass of the earth is about [math]10^{27}[/math] g [math]\approx 10^{50}[/math] atoms, so a carbon atom with an energy of 5 eV would be difficult to observe in a detector the size of the earth .

The average energy we expect to see would be calculated by

[math]\lt E\gt = \int_{0}^{\infty} E \cdot P(E) dE[/math]

If you used this block of carbon as a detector you would easily notice an event in which a carbon atom absorbed 5 eV of energy as compared to the energy of a typical atom in the carbon block.

---

Silicon detectors and Ionization chambers are two commonly used devices for detecting radiation.

approximately 1 eV of energy is all that you need to create an electron-ion pair in Silicon

[math]P(E=1 eV) = e^{-1/0.0258} \approx 10^{-17}[/math]

approximately 10 eV of energy is needed to ionize an atom in a gas chamber

[math]P(E=10 eV) = e^{-10/0.0258} \approx 10^{-169}[/math]

The low probability of having an atom with 10 eV of energy means that an ionization chamber would have a better Signal to Noise ratio (SNR) for detecting 10 eV radiation than a silicon detector

But if you cool the silicon detector to 200 degrees Kelvin (200 K) then

[math]P(E=1 eV) = e^{-1/0.0172} \approx 10^{-26} \lt \lt 10^{-17}[/math]

So cooling your detector will slow the atoms down making it more noticable when one of the atoms absorbs energy.

also, if the radiation flux is large, more electron-hole pairs are created and you get a more noticeable signal.

Unfortunately, with some detectore, like silicon, you can cause radiation damage that diminishes it's quantum efficiency for absorbing energy.

What does this have to do with Simulations?

You just did a SImulation. Consider the following description of the Monte Carlo Method

The Monte Carlo method

Stochastic

from the greek word "stachos"

a means of, relating to, or characterized by conjecture and randomness.

A stochastic process is one whose behavior is non-deterministic in that the next state of the process is partially determined.

The above particle detector was an example of describing a stochastic process using a probability distribution to determine the likely hood of finding an atom with a certain energy.

Physics at the Quantum Mechanics scale contains some of the clearest examples of such a non-deterministic systems. The canonical systems in Thermodynamics is another example.

Basically the monte-carlo method uses a random number generator (RNG) to generate a distribution (gaussian, uniform, Poission,...) which is used to solve a stochastic process based on an astochastic description.

Example 2 Calculation of [math]\pi[/math]

Astochastic description

[math]\pi[/math] may be measured as the ratio of the area of a circle of radius [math]r[/math] divided by the area of a square of length [math]2r[/math]

File:PI from AreaRatio.jpg[math]\frac{A_{circle}}{A_{square}} = \frac{\pi r^2}{4r^2} = \frac{\pi}{4}[/math]

You can measure the value of [math]\pi[/math] if you physically measure the above ratios.

Stochastic description

Construct a dart board representing the above geometry, throw several darts at it, and look at a ratio of the number of darts in the circle to the total number of darts thrown (assuming you always hit the dart board).

Monte-Carlo Method

Here is an outline of a program to calulate [math]\pi[/math] using the Monte-Carlo method with the above Stochastic description

begin loop
 x=rnd
 y=rnd
 dist=sqrt(x*x+y*y)
 if dist <= 1.0 then numbCircHits+=1.0
 numbSquareHist += 1.0
end loop
 print PI = 4*numbCircHits/numbSquareHits

A Unix Primer

To get our feet wet using the UNIX operating system, we will try to solve example 2 above using a RNG under UNIX

List of important Commands

1. ls
2. pwd
3. cd
4. df
5. ssh
6. scp
7. mkdir
8. printenv
9. emacs, vi, vim
10. make, gcc
11. man
12. less
13. rm

---

Most of the commands executed within a shell under UNIX have command line arguments (switches) which tell the command to print information about using the command to the screen. The common forms of these switches are "-h", "--h", or "--help"

ls --help
ssh -h

the switch deponds on your flavor of UNIX

if using the switch doesn't help you can try the "man" (sort for manual) pages (if they were installed). Try

man -k pwd

the above command will search the manual for the key word "pwd"

Example 3: using UNIX to compile a RNG

Step

1. login to minerve.
   click here for a description of logging in if using windows otherwise (ssh username@minerve.cose.isu.edu)
2. mkdir src
3. cd src
4. scp -r foretony@minerve.cose.isu.edu:src/PI ./
5. ls
6. cd PI
7. make
8. ./PI_MC

Here is a web link to the source files you can copy in case the above doesn't work in this case the final command is "./rnd_test"

A Root Primer

In bash shell do

export ROOTSYS=~tforest/src/ROOT/root

if chsh do

setenv ROOTSYS ~tforest/src/ROOT/root

To start the root program type

$ROOTSYS/bin/root

another method

source ~foretony/src/ROOT/root/bin/thisroot.sh

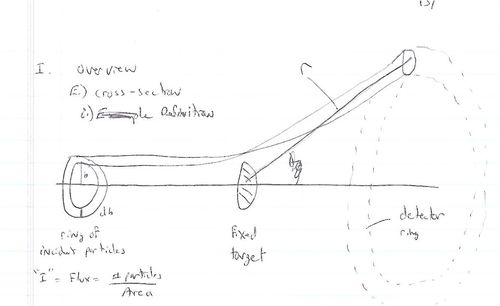
Cross Sections

Definitions

Total cross section

[math]\sigma \equiv \frac{\# \mbox{ particles scattered}} {\frac{ \# \mbox{ incident particles}}{\mbox{Area}}}[/math]

Differential cross section

[math]\sigma(\theta)[/math] = [math] \frac{d \sigma}{d \Omega} \equiv \frac{\frac{\# \mbox{ particles scattered}}{\mbox{solid angle}}} {\frac{ \# \mbox{incident particles}}{\mbox{Area}}}[/math]

Solid Angle

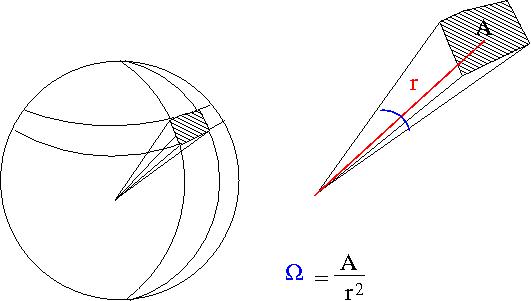
[math]\Omega[/math]= surface area of a sphere covered by the detector

ie;the detectors area projected onto the surface of a sphere

A= surface area of detector

r=distance from interaction point to detector

[math]\Omega = \frac{A}{r^2} sr [/math]

[math]sr \equiv[/math] steradians

[math]A_{\mbox{sphere}} = 4 \pi r^2[/math] if your detector was a hollow ball

[math]\Omega_{\mbox{max}} = \frac{4 \pi r^2}{r^2} = 4\pi[/math]steradians

Units

Cross-sections have the units of Area

1 barn = [math]10^{-28} m^2[/math]

[units of [math]\sigma(\theta)[/math]] =[math]\frac{\frac{[\mbox{particles}]}{[\mbox{steradian}]}} {\frac{ [ \mbox{particles}]}{[m^2]}} = m^2[/math]

Luminosity

[math]L = \frac{\mbox{Number of Scatterers}}{\mbox{Area} \cdot \mbox{time}} \sim i_{\mbox{beam}} \rho_{\mbox{target}} l_{\mbox{target}}[/math]

Fixed target scattering

[math]N_{in}[/math]= # of particles in = [math]I \cdot A_{in}[/math]

[math]A_{in}[/math] is the area of the ring of incident particles

[math]dN_{in} = I \cdot dA = I (2\pi b) db[/math]= # particles in a ring of radius [math]b[/math] and thickness [math]db[/math]

You can measure [math]\sigma(\theta)[/math] if you measure the # of particles detected [math]d N[/math] in a known detector solid angle [math]d \Omega[/math] from a known incident particle Flux ([math]I[/math]) as

[math]\sigma(\theta) = \frac{\frac{d N}{ d \Omega}}{I}[/math]

Alternatively if you have a theory which tells you [math]\sigma(\theta)[/math] which you want to test experimentally with a beam of flux [math]I[/math] then you would measure counts (particles)

[math]dN = I \sigma(\theta) d \Omega = I \sigma(\theta) \frac{d A}{r^2} = I \sigma(\theta) \frac{r^2 \sin(\theta) d \theta d \phi}{r^2}[/math]

Units

[math][d N] = [\frac {\mbox{particles}}{m^2}][m^2] [\mbox{steradian}] [/math] = # of particles

or for a count rate divide both sides by time and you get beam current on the RHS

integrate and you have the total number of counts

Classical Scattering

In classical scattering you get the same number of particles out that you put in (no capture, conversion,..)

[math]d N_{in} = dN[/math]

[math]d N_{in} = I dA = I (2\pi b) db[/math]

[math]d N = I \sigma(\theta) d \Omega = I \sigma(\theta) \sin(\theta) d \theta d \phi = I \sigma(\theta) \sin(\theta) d \theta (2 \pi )[/math]

[math] I (2\pi b) db = I \sigma(\theta) \sin(\theta) d \theta (2 \pi )[/math]

[math] b db = \sigma(\theta) \sin(\theta) d \theta [/math]

[math]\sigma(\theta) = \frac{b}{\sin(\theta)}\frac{db}{d \theta}[/math]

[math]\frac{db}{d \theta}[/math] tells you how the impact parameter [math]b[/math] changes with scattering angle [math]\theta[/math]

Example 4: Elastic Scattering

This example is an example of classical scattering.

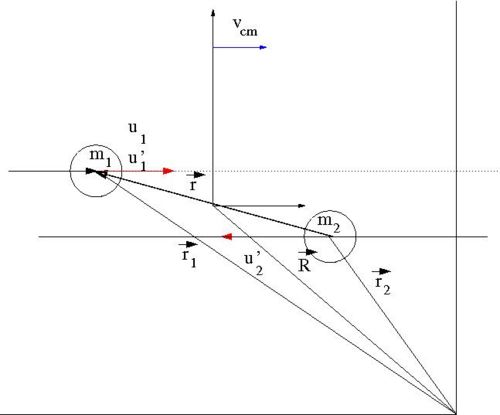
Our goal is to find [math]\sigma(\theta)[/math] for an elastic collision of 2 impenetrable spheres of diameter [math]a[/math]. We need to look for a relationship between the impact parameter [math] b[/math] and the scattering angle [math] \theta[/math]. To find this relationship, let's solve this elastic scattering problem by describing the collision using the Center of Mass (C.M.) coordinate system in terms of the reduced mass. As we shall see, the 2-body collision becomes a 1-body problem when a C.M. coordinate system is used. Then we will describe the motion of the reduced mass in the C.M. Frame.

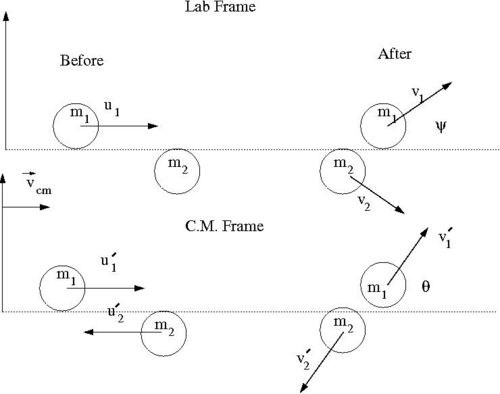Media:SPIM_ElasCollis_Lab_CM_Frame.xfig.txt

Variable definitions

[math]b[/math]= impact parameter ; distance of closest approach

[math]m_1[/math]= mass of incoming ball

[math]m_2[/math]= mass of target ball

[math]u_1[/math]= iniital velocity of incoming ball in Lab Frame

[math]v_1[/math]= final velocity of [math]m_1[/math] in Lab Frame

[math]\psi[/math]= scattering angle of [math]m_1[/math] in Lab frame after collision

[math]u_1^{\prime}[/math]= iniital velocity of [math]m_1[/math] in C.M. Frame

[math]v_1^{\prime}[/math]= final velocity of [math]m_1[/math] in C.M. Frame

[math]u_2^{\prime}[/math]= iniital velocity of [math]m_2[/math] in C.M. Frame

[math]v_2^{\prime}[/math]= final velocity of [math]m_2[/math] in C.M. Frame

[math]\theta[/math]= scattering angle of [math]m_1[/math] in C.M. frame after collision

Determining the reduced mass

vector definitions

[math]\vec{r}_1[/math] = a position vector pointing to the location of [math]m_1[/math]

[math]\vec{r}_2[/math] = a position vector pointing to the location of [math]m_2[/math]

[math]\vec{R}[/math] = a position vector pointing to the center of mass of the two ball system

[math]\vec{r} \equiv \vec{r}_1 - \vec{r}_2[/math] = the magnitude of this vector is the distance between the two masses

In the C.M. reference frame the above vectors have the following relationships

1. [math]\vec{R} = 0 = \frac{m_1 \vec{r}_1 + m_2 \vec{r}_2}{m_1 + m_2} \Rightarrow m_1 \vec{r}_1 = -m_2 \vec{r}_2[/math]
2. [math]\vec{r}_1 - \vec{r}_2 = \vec{r}[/math]

solving the above equations for [math]\vec{r_1}[/math] and [math]\vec{r_2}[/math] and defining the reduced mass [math]\mu[/math] as

[math]\mu = \frac{m_1 \cdot m_2}{m_1 + m_2} \equiv[/math] reduced mass

leads to

[math]\vec{r}_1 = \frac{\mu}{m_1} \vec{r}[/math]

[math]\vec{r}_2 = -\frac{\mu}{m_2} \vec{r}[/math]

We can use the above reduced mass relationships to construct the Lagrangian in terms of [math]\vec{r}[/math] instead of [math]\vec{r}_1[/math] and [math] \vec{r}_2[/math] thereby reducing the problem from a 2-body problem to a 1-body problem.

Construct the Lagrangian

The Lagrangian is defined as:

[math]\mathcal{L} = T - U[/math]

where

[math]T \equiv[/math] kinetic energy of the system

[math]U \equiv[/math] Potential energy of the system which describes the interaction

[math]\mathcal{L} = \frac{1}{2} |\vec{\dot{r}}_1|^2 + \frac{1}{2} |\vec{\dot{r}}_2|^2 - U[/math]

= [math]\frac{1}{2} m_1 \left (\frac{m_2}{m_1+m_2} \right )^2 |\vec{\dot{r}}|^2 + \frac{1}{2} m_2 \left (\frac{m_1}{m_1+m_2} \right )^2 |\vec{\dot{r}}|^2 -U(\vec{r})[/math]

= [math]\frac{1}{2} \left ( m_2 + m_1 \right ) \left (\frac{m_1m_2}{(m_1+m_2)^2} \right ) |\vec{\dot{r}}|^2 -U(\vec{r})[/math]

after substituting derivative of the expressions for [math]\vec{r_1}[/math] and [math]\vec{r}_2[/math]

= [math]\frac{1}{2} \mu |\vec{\dot{r}}|^2 -U(\vec{r})[/math]

The 2-body problem is now described by a 1-body Lagrangian we need to determine which coordinate system (cartesian, spherical,..) to use to write an expression for ([math]|\vec{\dot{r}}|^2[/math]). Polar seems best unless there is a dependence in the azimuthal angle.

Lagranges equations of motion are given by

[math]\frac{\partial \mathcal{L}}{\partial q} = \frac{d}{dt} \frac{\partial \mathcal{L}}{\dot{q}}[/math]

where [math]q[/math] represents one of the coordinate (cannonical variables).

To get the classical scattering cross section we are interested in finding an expression for the dependence of the impact parameter on the scattering angle,[math]\frac{d b}{d \theta}[/math].

Now lets redraw the collision in terms of a reference frame fixed on [math]m_2[/math] (before collision its the Lab Frame but not after collision).

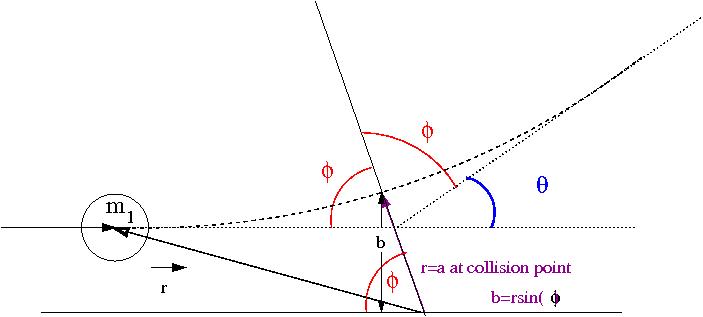Media:SPIM_ElasColls_CMFrame_xfig.txt

The C.M. Frame rides along the center of mass, the above coordinate system though has its origin on [math]m_2[/math]. The above drawing identifies [math]\theta[/math] and [math]\phi[/math] for the system at the point of the collision in which the CM frame is a distance [math]a[/math] (the size of the ball) from the origin of the coordinate system fixed to [math]m_2[/math]. If [math]b \gt a[/math] then there is no collision ([math]\theta=0[/math]), otherwise a collision happens when r=a (the distance between the balls is equal to their diameter). A head on collision is defined as [math]b=0[/math] ([math]\theta=\pi[/math]).

Observation

as [math]\theta[/math] gets smaller, [math]b[/math] gets bigger

[math]\frac{d b}{d \theta} \lt 0[/math]

Using plane polar coordinates ([math]r, \phi[/math]) we can describe the problem in the lab frame as:

[math]\vec{v} = \dot{r} \hat{e}_r + r \dot{\phi} \hat{e}_{\phi}[/math]

[math]T = \frac{1}{2} \mu ( \dot{r}^2 + r^2 \dot{\phi}^2)[/math]

[math]U(r) = \left \{ {0 \; r \gt a \atop \infty \; r \le a} \right .[/math]

[math]\mathcal{L} = T -U = \frac{1}{2} \mu ( \dot{r}^2 + r^2 \dot{\phi}^2) - U(r)[/math]

Lagranges Equation of Motion:

[math]\frac{\partial \mathcal {L}}{\partial \phi} = \frac{d}{d t} \frac{\partial \mathcal{L}}{\partial \dot{\phi}}[/math] [math]0 = \frac{d}{d t} [ \mu r^2 \dot{\phi}] \Rightarrow[/math] there is a constant of motion ( Constant angular momentum)

[math]\ell \equiv \mu r^2 \dot{\phi} = \vec{r} \times \vec{p} = \vec{r} \times \mu \vec{v} = r^2 \mu \dot{\phi}[/math]

substitute [math]\ell[/math] into [math]\mathcal{L}[/math]

[math]\mathcal{L} = \frac{1}{2} ( \mu \dot{r}^2 + \frac{\ell}{\mu r^2} ) - U(r)[/math]

The two equations above are in terms of [math]r[/math] and [math]\phi[/math] whereas our goal is to find an expression for [math]\frac{ d b}{ d \theta}[/math]. Since [math]r[/math] is related to [math]b[/math] and [math]\phi[/math] is related to[math] \theta[/math] ([math]\theta = \pi - 2\phi[/math]; see figure above) we should try and find expressions for [math]d \phi[/math] in terms of [math]r(b)[/math]

Trick

[math]\dot{\phi} = \frac{d \phi}{d t} = \frac{d \phi}{d r} \frac{d r}{d t}[/math]

[math]\Rightarrow \ell = \mu r^2 \frac{d \phi}{d r} \dot{r}[/math]

or

[math]d \phi = \frac{\ell}{\mu r^2 \dot{r}} dr[/math]

We now need an expression for [math]\dot{r}[/math] in order to integrate the above equation to determine the functional dependence of [math]\phi[/math] and hence[math] \theta[/math].

The potential in the Lagrangian though is infinite for [math]r \le a[/math] . Let's use the property of conservation of energy to accommodate this mathematical construct.

Since Energy is conserved (Elastic Scattering), we may define the Hamiltonian as

[math]H = T + U = \frac{1}{2} (\mu \dot{r}^2 + \frac{\ell}{\mu r^2}) + U(r) = constant \equiv E[/math]

solving for [math]\dot{r}[/math]

[math]\dot{r} = \pm \sqrt{\frac{2(E-U(r))}{\mu} - \frac{\ell^2}{\mu^2 r^2}}[/math]

substituting the above into the equation for [math]d \phi[/math] and integrating:

[math]\phi = \int d \phi = \int_{r_{min}}^{r_{max}} \frac{\ell}{\mu r^2 \dot{R}} dr[/math]

[math]r_{min} = a \; \; \; r_{max}= \infty \; \; \; U(r) = 0 : a \le r \le \infty[/math]

[math]\phi = \int_a^{\infty} \frac{\ell} {r^2 \sqrt{2 \mu E - \frac{\ell^2}{r^2}} }dr[/math]

For [math]a \le r \le \infty[/math] : [math]E = \frac{1}{2} \mu v^2_{cm} \Rightarrow v_{cm} = \sqrt{\frac{2E}{\mu}}[/math]

[math]\vec{\ell} = \vec{r} \times \vec{p} \Rightarrow |\vec{\ell}| = |\vec{r}| |\vec{p}| \sin(\phi) = r \mu v_{cm} \sin(\phi) = r \mu \left ( \sqrt{\frac{2E}{\mu}} \right) \sin(\phi) = \sqrt{2 \mu E} r\sin(\phi) =\sqrt{2 \mu E} b[/math]

substituting this expression for [math]\ell[/math] into the last expression for [math]\phi[/math] above :

[math]\phi =\int_a^{\infty} \frac{b dr}{r\sqrt{(r^2-b^2)}}[/math]

Integral Table

[math]\int \frac{dx}{x\sqrt{(\alpha x^2+\beta x+\gamma)}} = \frac{-1}{\sqrt{-\gamma}} \sin^{-1} \left (\frac{\beta x+2\gamma}{|x|\sqrt{\beta^2-4\alpha \gamma}} \right )[/math]

let [math]x=r \;\; \alpha=1 \;\; \beta=0 \;\; \gamma=-b^2[/math]

then

[math]\phi = \left . b \frac{1}{\sqrt{-(-b^2)}} \sin^{-1} \left (\frac{-2b^2}{r\sqrt{0-4(1)(-b^2) } }\right ) \right |_a^{\infty} = \sin^{-1} (0)- \sin^{-1}(-\frac{b}{a})[/math]

or

[math]\sin(\phi) = \frac{b}{a} = \sin \left ( \frac{\pi}{2} - \frac{\theta}{2} \right ) = \cos \left ( \frac{\theta}{2} \right )[/math]

[math]\Rightarrow b = a \cos \left( \frac{\theta}{2} \right)[/math]

Now substitute the above into the expression for [math]\sigma(\theta)[/math]

[math]\sigma(\theta) = \frac{b}{\sin(\theta)} \frac{d b}{d \theta} = \frac{a \cos(\theta/2)}{sin(\theta)} a[-\sin(\theta/2)]\frac{1}{2} = \frac{a^2}{2} \frac{\cos(\theta/2) \sin(\theta/2)}{\sin(\theta)}[/math]

drop the negative sign, sqrt in denominator allows this, and use the trig identity

[math]\sin \left (\frac{\theta}{2} + \frac{\theta}{2} \right ) = \cos \left (\frac{\theta}{2} \right) \sin \left (\frac{\theta}{2} \right ) + \cos \left ( \frac{\theta}{2} \right ) \sin \left (\frac{\theta}{2} \right )[/math]

[math]\sin(\theta) = 2 \cos \left (\frac{\theta}{2} \right ) \sin \left (\frac{\theta}{2} \right )[/math]

[math]\sigma(\theta) = \frac{a^2}{2} \frac{1}{2} = \frac{a^2}{4}[/math]

[math]\sigma = \int \sigma(\theta) d \Omega = \frac{a^2}{2} \frac{1}{2} 4 \pi = \pi a^2[/math]

compare with result from definition

[math]\sigma[/math] = scattering cross-section [math]\equiv \frac{\# particles\; scattered} {\frac{ \# incident \; particles}{Area}}[/math]

number of particles scattered = number of incident particles

Area = [math] \pi a^2[/math] = The area profile in which a collision occurs( the ball diameter is [math]a[/math])

[math]\sigma = \frac{{N}}{\frac{ N}{\pi a^2}} = \pi a^2[/math]

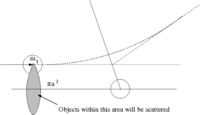
Lab Frame Cross Sections

The C.M. frame is often chosen to theoretically calculate cross-sections even though experiments are conducted in the Lab frame. In such cases you will need to transform cross-sections between two frames.

The total cross-section should be frame independent

[math]\sigma_{C.M.} = \sigma_{Lab}[/math]

or

[math]\sigma(\theta) d \Omega = \sigma(\psi) d \Omega^{\prime}[/math]

where

[math]\theta[/math] is in the CM frame and [math]\psi[/math] is in the Lab frame.

A non-relativistic transformation

[math]\sigma(\theta) d \Omega = \sigma(\psi) d \Omega^{\prime}[/math]

[math]\sigma(\theta) 2 \pi \sin(\theta) d \theta = \sigma(\psi) 2 \pi \sin (\psi) d \psi[/math]

[math]\Rightarrow \sigma(\psi) = \frac{\sin(\theta)}{\sin(\psi)} \frac{d \theta}{d \psi} \sigma(\theta)[/math]

The transformation is governed by the dependence of [math]\theta[/math] on [math] \psi[/math] [math] \left( \frac{d \theta}{d \psi} \right )[/math]

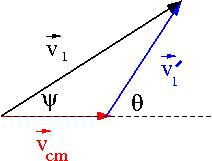
Lets return back to our picture of the scattering Process

if we superimpose the vectors [math]\vec{v}_1[/math] and [math]\vec{v}_1^{\prime}[/math] we have

Trig identities (non-relativistic Gallilean transformation) tell us

[math]v_1 \sin(\psi) = v_1^{\prime} \sin(\theta)[/math]

[math]v_1 cos(\psi) = v_{cm} + v_1^{\prime} \cos(\theta)[/math]

solving for [math]\psi[/math]

[math]\tan(\psi) = \frac{\sin(\psi)}{\cos(\psi)} = \frac{v_1^{\prime} \sin(\theta)/v_1}{\frac{v_{CM}}{v_1} + \frac{v_1^{\prime} \cos(\theta)}{v_1} } = \frac{\sin(\theta)}{\cos(\theta) + \frac{v_{CM}}{v_1^{\prime}}}[/math]

For an elastic collision only the directions change in the CM Frame: [math]u_1^{\prime}= v_1^{\prime}[/math] & [math]u_1^{\prime}= v_2^{\prime}[/math]

From the definition of the C.M.

[math]\vec{v}_{CM} = \frac{m_1 \vec{u}_1 + m_2 \vec{u}_2}{m_1+m_2} = \frac{m_1}{m_1+m_2} \vec{u}_1[/math]

conservation of momentum in CM Frame [math]\Rightarrow[/math]

[math]m_1 u_1^{\prime} = - m_2 u_2{\prime}[/math]

[math] \Rightarrow v_1^{\prime} = u_1^{\prime} = \frac{-m_2}{m_1} u_2^{\prime}[/math]

Gallilean Coordinate transformation

[math]\vec{u}_1 = \vec{u}_1^{\prime} + \vec{v}_{CM} = \vec{u}_1^{\prime} + \frac{m_1}{m_1+m_2} \vec{u}_1[/math]

[math]\Rightarrow u_1{\prime} = \left [ 1 - \frac{m_1}{m_1 + m_2} \right ] u_1 = \frac{m_2}{m_1+m_2}u_1[/math]

[math]\Rightarrow v_1^{\prime} = u_1^{\prime} =\frac{m_2}{m_1+m_2} u_1[/math]

another expression for [math]\psi[/math]

using the above gallilean transformation we can do the following

[math]\frac{v_{CM}}{v_1^{\prime}}= \frac{\frac{m_1}{m_1+m_2} u_1}{\frac{m_2}{m_1+m_2} u_1} = \frac{m_1}{m_2}[/math]

or

[math]\tan(\psi) = \frac{\sin(\theta)}{\cos(\theta) + \frac{m_1}{m_2}}[/math]

after a little trig substitution

[math]\Rightarrow \frac{m_1}{m_2} = \frac{sin(\theta - \psi)}{\sin(\psi)} =[/math] constant

now use the chain rule to find [math]\frac{d \theta}{d \psi}[/math]

[math]f \equiv \frac{sin(\theta - \psi)}{\sin(\psi)} =[/math] constant

[math]df = 0 = \frac{ \partial f}{\partial \psi} d \psi + \frac{ \partial f}{\partial \theta} d \theta [/math]

[math]\Rightarrow \frac{d \theta}{d \psi} = \frac{-\frac{ \partial f}{\partial \psi} }{\frac{ \partial f}{\partial \theta} }[/math]

[math]-\frac{ \partial f}{\partial \psi} = \frac{\cos(\theta - \psi)}{\sin(\psi)} + \frac{\sin(\theta - \psi)}{\sin(\psi)}[/math]

[math]\frac{ \partial f}{\partial \theta }= 1 + \frac{\sin(\theta - \psi) \cos(\psi)}{\cos(\theta - \psi) \sin(\psi)}[/math]

after substitution:

[math]\sigma(\psi) = \frac{\sin(\theta)}{\sin(\psi)} \frac{d \theta}{d \psi} \sigma(\theta)[/math]

[math]=\frac{\sin(\theta)}{\sin(\psi)} \left [ 1 + \frac{\sin(\theta - \psi) \cos(\psi)}{\cos(\theta - \psi) \sin(\psi)} \right ] \sigma(\theta)[/math]

For the above equation to be more useful one would prefer to recast it in terms of only [math]\psi[/math] and masses.

[math]\sigma(\psi) = \frac{\left [ \frac{m_1}{m_2}\cos(\psi) + \sqrt{1-\left ( \frac{m_1 \sin(\psi) }{m_2} \right )^2 }\right ]}{\sqrt{1 - \left ( \frac{m_1 \sin(\psi)}{m_2}\right )^2 }}\sigma(\theta)[/math]

Simulations_of_Particle_Interactions_with_Matter