Inverting OP Amp

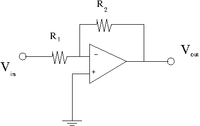
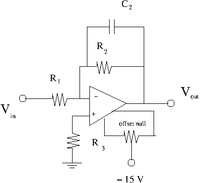
1. Construct the inverting amplifier according to the wiring diagram below.

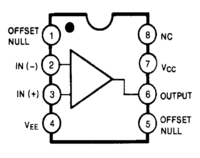
Here is the data sheet for the 741 Op Amp

Use [math]R_1 = 1k\Omega[/math] and [math]R_2 = 10 k\Omega[/math] as starting values.

2. Insert a 0.01 [math]\mu[/math]F capacitor between ground and both Op Amp power supply input pins. The Power supply connections for the Op amp are not shown in the above circuit diagram, check the data sheet.

Gain measurements

1.) Measure the gain as a function of frequency between 100 Hz and 2 MHz for three values of [math]R_2[/math] = 10 k[math]\Omega[/math], 100 k[math]\Omega[/math], 1M[math]\Omega[/math]. Keep [math]R_1[/math] at [math]1k\Omega[/math].

2.)Graph the above measurements with the Gain in units of decibels (dB) and with a logarithmic scale for the frequency axis.

One of the practical op-amp limitations is that the open loop gain which is so high at frequencies in the kHz range (100,000 to a million or more) drops to a gain of one at some high frequency (say 1 to 10 MHz). Many op-amps contain internal compensation to cause a 6dB per octave rolloff of gain (like a low-pass filter) at some chosen frequency to stabilize the unit against high frequency oscillations. For the 741 this rolloff starts at 100 kHz. From the beginning of the rolloff the RC type filter action leads to phase shift starting at 90¡ and increasing to 120¡ to 160¡ as the gain approaches one. If the phase shift reaches 180¡ the feedback becomes positive and the system can oscillate.

Impedance

Input Impedance

Measure [math]R_{in}[/math] for the 10 fold and 100 fold amplifier at ~100 Hz and 10 kHz frequency.

For the 741 the input resistance measured to one input with the other grounded is about 2 Megohms.

There is a tiny input bias current for an op-amp which is about 80 nA for 741 type op-amps.

[math]V_{in} [/math](V)	[math]I_{in} [/math](A)

Output Impedance

Measure [math]R_{out}[/math] for the 10 fold and 100 fold amplifier at ~100 Hz and 10 kHz frequency. Be sure to keep the output ([math]V_{out}[/math]) undistorted

To show that the output impedance is small, observe the gain at f = 1 kH z with an output load of 10 Ω. Note that the maximum output current of the 411 is about 20 mA, so limit the output voltage to less than 200 mV .

For the 741 it is about 75 ohms but can be as high as several thousand ohms for some low power op-amps. The effective output impedance is further lowered by the use of negative feedback, so the focus becomes not one of the number of ohms looking into the output, but what limitations are placed on the output current. Limiting the output current also limits the allowable output voltage swing: the lower the load resistance, the lower the allowable voltage amplitude. For a load >2K, the 741 can swing to within about 2 volts of the supply. This is about all that is permitted by common mode limits for a 15 volt supply so the output impedance is not a serious limitation.

[math]V_{io}[/math] and [math]I_{B}[/math]

Use the above equation and two measurements of [math]V_{out}[/math], [math]R_1[/math], and [math]R_2[/math] to extract [math]V_{io}[/math] and [math]I_B[/math].

measure [math]V_{out}[/math] for [math]R_1[/math] = 1 k[math]\Omega[/math], [math]R_2[/math] = 100 k[math]\Omega[/math], and[math] V_{in}[/math]=0 (grounded).
measure [math]V_{out}[/math] for [math]R_1[/math] = 10 k[math]\Omega[/math], [math]R_2[/math] = 1 M[math]\Omega[/math], and[math] V_{in}[/math]=0 (grounded).
You can now construct 2 equations with 2 unknowns [math]V_{io}[/math] and [math]I_B[/math].

[math]I_{io}[/math]

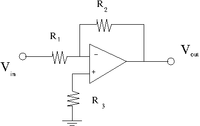
Now we will put in a pull up resistor as shown below.

Instead of the current [math]I_B[/math] we have the current [math]I_{io}[/math]

Use the same technique and resistors from the previous section to construct 2 equations and 2 unknowns and extract [math]I_{io}[/math], keep [math]V_{in}[/math]=0.

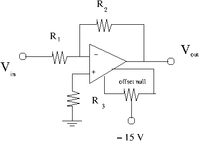
The offset Null Circuit

Construct the offset null circuit above.
Adjust the potentiometer to minimize [math]V_{out}[/math] with [math]V_{in}=0[/math].
Use a scope to measure the output noise.

One of the practical op-amp limitations is that the input bias currents for the two inputs may be slightly different. Even though the inputs are designed to be symmetrical, slight differences which occur in the manufacturing process may give slightly different bias currents. This offset current is typically on the order of a tenth of the input bias current, with 10nA being a representative offset current for a 741.

Even with identical source impedances, this offset current will produce a slight voltage between the input terminals, contrary to the ideal voltage rule.

Capacitors

Revert back to the pull up resistor

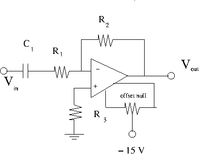
Capacitor in parallel with [math]R_2[/math]

Select a capacitor such that when [math]\omega[/math]= 10 kHz.
Add the capacitor in parallel to [math]R_2[/math] so you have the circuit shown above.
Use a pulse generator to input a sinusoidal voltage [math]V_{in}[/math]
Measure the Gain as a function of the [math]V_{in}[/math] frequency and plot it.

Capacitor in series with R_1

Select a capacitor such that when [math]\omega[/math]= 1 kHz.
Add the capacitor in series to [math]R_1[/math] so you have the circuit shown above.
Use a pulse generator to input a sinusoidal voltage [math]V_{in}[/math]
Measure the Gain as a function of the [math]V_{in}[/math] frequency and plot it.

Slew rate

Measure the slew and compare it to the factory spec.

The slew rate for the 741 is 0.5V/microsecond compared to 100V/microsecond for a high-speed op-amp. The slew-rate imposes high-frequency limitations on the device. At some critical frequency, an output swing equal to the supply voltages will require a slew rate faster than the maximum slew rate of the device. Above that frequency, the amplitude of distortion-free output voltage swing will be limited.

Power Supply Rejection Ratio

Set V_{in} = 0.
Measure [math]V_{out}[/math] while changing [math]V_{cc}[/math]

Output voltage RMS noise [math]\Delta V_{out}^{RMS}[/math]

Forest_Electronic_Instrumentation_and_Measurement

TF EIMLab23 Writeup

Contents