TF 01092012 Colloq

Title: Inelastic Physics Asymmetries

Abstract

ISU's intermediate energy nuclear physics group is presently involved in several fundamental physics measurements. This talk will describe two measurements that use inelastic polarized electron scattering. The first measurement investigates the response of the nucleon's first excited state, the Delta resonance, to polarized electromagnetic probes. The excitation of the nucleon to its first excited state is commonly described in terms of a quark spin flip induced by an electromagnetic probe. Recently, however, there has been increasing interest in a second method that uses a different neutral particle called the Z-boson to induce the quark spin flip via the Weak force. A fundamental constant known as d-delta can be measured using this interaction. A second program to measure quark polarization distributions by looking at the response of a polarized nucleon to a polarized electron is also underway. This program will test the predictions of a fundamental theory known as quantum-chromodynamics. The physics implications of these experiments and the roles of graduate students in the physics program will be described.

Intro

1. Inelastic Asymmetry Measurements
2. Graduate Student Projects
3. Future efforts

ISU Physics Measurements

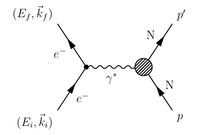
Kinematics

Virtual Photon Q^2

Using Ryder 4-momentum tensor convention: [math]P_{\mu} \equiv (E/c, -\vec{p}) \;\;\;\;\; P^{\mu} \equiv (E/c, \vec{p})[/math]

[math]q_\mu \equiv (\omega, \vec{q})[/math] [math]k^i_\mu \equiv (E_i, \vec{k_i})[/math] [math]k^f_\mu \equiv (E_f, \vec{k_f})[/math]

Conservation of Momentum

[math] k^i_\mu =q_\mu + k^f_\mu [/math]

Momentum Transfer

[math] q_\mu =k^i_\mu - k^f_\mu [/math]

Momentum Transfer Squared

[math] -Q^2 = q^2 = q_\mu q^{\mu} =(E_i-E_f)^2 - (\vec{k}_i - \vec{k}_f) \cdot (\vec{k}_i - \vec{k}_f) [/math]

[math]= m_i^2 + m_f^2 -2E_iE_f + 2\left | \vec{k}_i\right | \left | \vec{k}_f\right | cos(\theta)[/math]

[math]=-4E_iE_f \sin^2(\theta/2) \;\;\; m_i = m_f \ll E_i \mbox{ and } E \approx \left | \vec{k}_i\right |[/math]

[math]Q^2 =4E_iE_f \sin^2(\theta/2) \gt 0[/math] A space-like scattering event

Space-like interval: Two events are separated by a space like interval then there isn't enough time passing between them to allow a cause-effect relationship because a photon can't traverse the distance. This means that there is no reference frame that may be used to describe the event as happening at the same spatial location but there is a frame that describes them happening at the same time. If the spacetime interval between the two events is defined as s[math]^2 = (\Delta r)^2 - (c\Delta t)^2[/math] then [math]s^2 \gt 0[/math] for a space-like interval

Time-like interval: Two events are separated by a time like interval if enough time passes between them to allow a cause-effect relationship. This means that there is no reference frame that may be used to describe the event as happening at the same time but there is one that describes them happening at the same spatial location. If the spacetime interval between the two events is defined as s[math]^2 = (\Delta r)^2 - (c\Delta t)^2[/math] then [math]s^2 \lt 0[/math] for a time-like interval

Inclusive Missing mass W**2

Inelastic scattering (Energy is not conserved but absorbed from the momentum transfer)

[math]P_e^{\mu} \equiv (E_i,\vec{k}_i)[/math] [math]\left(P_e^{\mu}\right)^{\prime} \equiv (E_f,\vec{k}_f)[/math] [math]P_p^{\mu} \equiv (M_p,0)[/math] [math]\left(P_p^{\mu}\right)^{\prime} \equiv (E_X,\vec{k}_X)[/math]

4-momentum conservation

[math]P_e^{\mu} + P_p^{\mu} = \left(P_e^{\mu}\right)^{\prime} + \left(P_p^{\mu}\right)^{\prime}[/math]

[math]\left(P_p^{\mu}\right)^{\prime} \left(P_{\mu}^p\right)^{\prime} = [P_e^{\mu} + P_p^{\mu} - \left(P_e^{\mu}\right)^{\prime} ][P^e_{\mu} + P^p_{\mu} - \left(P^e_{\mu}\right)^{\prime} ][/math]

[math]E_X^2 - P_X^2 \equiv W^2 = (E_i^2 - k_i^2) + (E_f^2-k_f^2) + M_p^2 + 2M_p(E_i - E_f) -2(E_iE_f-\vec{k_i}\cdot \vec{k_f})[/math]

[math]W^2=M_p^2 + 2M_p(E_i-E_f) -Q^2 \equiv [/math]Invariant Missing Mass = mass of the intermediate state that was created.

200 px

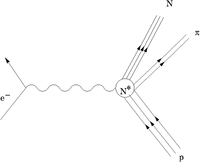
The Delta Resonance

Decay Modes: [math]ep \rightarrow \;\; \left \{ {N \pi \;\;\; 99.5% \atop p \gamma \;\;\; 0.5% } \right .[/math]

[math]\sigma = \lt \Delta^+ | V_{\mu}^3| p\gt [/math]

[math]V_{\mu}^3 =[/math] Vector current of the virtual photon exchange

Double Spin Asymmetry

If both the target and the incident virtual photon are polarized then one can measure the cross-section for two separate conditions; when the spins are parallel and anti-parallel.

Let [math]\sigma_{3/2} [/math]

[math]\sigma_{1/2} \equiv[/math] photon helicity is anti-parallel to the target spin

[math]\sigma_{3/2} \equiv[/math] photon helicity is parallel to the target spin.

[math]\sigma_{\frac{1}{2}}[/math](Struck quark spin is [math]\parallel[/math] to Nucleon spin)	[math]\sigma_{\frac{3}{2}}[/math] (Struck quark spin is [math]\not\parallel[/math] to Nucleon spin)

Clebsch Gordan recoupling

The recoupling of two subsystems [math]\psi[/math] with angular momenta [math]j_1[/math] and [math]j_2[/math] to a new system[math] \Psi[/math] with total angular momentum [math]J[/math] is written as

[math]\Psi^{J}_{M} = \sum_{m_1=-j_1}^{j_1} \sum_{m_2=-j_2}^{j_2} C^{j_1\;,\;j_2,\;\;J}_{m_1,m_2,M} \; \psi^{j_1}_{m_1} \psi^{j_2}_{m_2}[/math] = expansion of the systems total angular momentum in terms of the uncoupled original basis states of each individual constituent

[math]\Psi^{3/2}_{3/2} = \sum_{m_1,m_2} C^{1,1/2,3/2}_{m_1,m_2,3/2} \psi^{1}_{m_1} \psi^{1/2}_{m_2} = C^{1,\frac{1}{2},\frac{3}{2}}_{1,\frac{1}{2},\frac{3}{2}}\psi^{1}_{1} \psi^{1/2}_{1/2} [/math] : all other possible m_1 and m_2 values don't add to M

[math]\Psi^{3/2}_{1/2} = \sum_{m_1,m_2} C^{1,1/2,3/2}_{m_1,m_2,1/2} \psi^{1}_{m_1} \psi^{1/2}_{m_2} = C^{1,\frac{1}{2},\frac{3}{2}}_{0,\frac{1}{2},\frac{1}{2}}\psi^{1}_{0} \psi^{1/2}_{1/2} + C^{1,\frac{1}{2},\frac{3}{2}}_{1,\frac{-1}{2},\frac{1}{2}}\psi^{1}_{1} \psi^{1/2}_{-1/2}[/math] : all other possible m_1 and m_2 values don't add to M

If I constrain the helicity of my virtual photon to be +1 by preparing electrons with spins along their direction of motion, then the state [math]\psi^{1}_{0}[/math] doesn't exist so only only one state enters the sum

[math]\Psi^{3/2}_{1/2} = C^{1,\frac{1}{2},\frac{3}{2}}_{1,\frac{-1}{2},\frac{1}{2}}\psi^{1}_{1} \psi^{1/2}_{-1/2}[/math] : all other possible m_1 and m_2 values don't add to M

[math]C^{j_1,j_2,J}_{m_1,m_2,M}[/math] : Clebsch-Gordon Coefficient [math]C^{1,\frac{1}{2},\frac{3}{2}}_{1,\frac{1}{2},\frac{3}{2}}=1[/math] [math]C^{1,\;\;\frac{1}{2},\frac{3}{2}}_{1,-\frac{1}{2},\frac{1}{2}}= \frac{1}{\sqrt{3}}[/math]

[math]A = \frac{\sigma_{\frac{1}{2}} - \sigma_{\frac{3}{2}}}{\sigma_{\frac{1}{2}} + \sigma_{\frac{3}{2}}} = \frac{\frac{1}{3} - 1}{\frac{1}{3} + 1} = -1/2[/math]

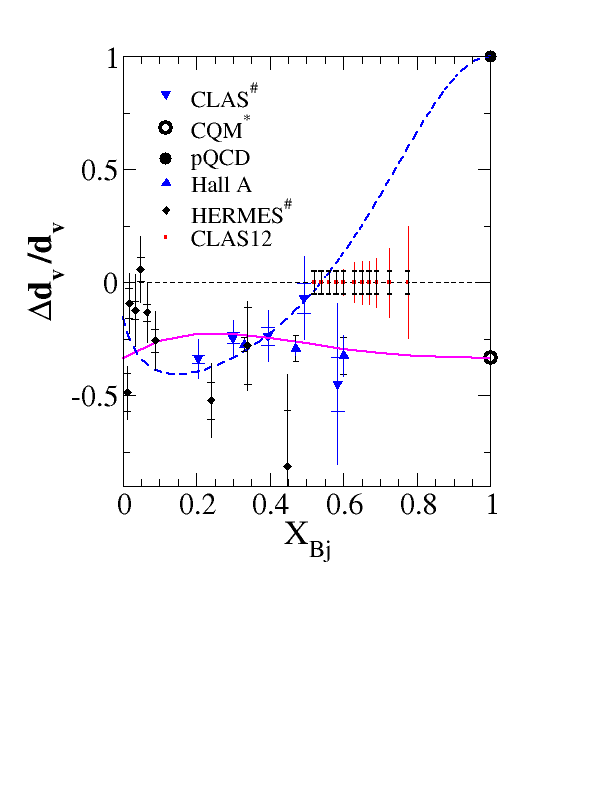
Quark Distributions

[math]\sigma_p^{\pi^+ \pm \pi^-} = \frac{1}{9}[4( u + \bar{u}) \pm ( d + \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\sigma_n^{\pi^+ \pm \pi^-} = \frac{1}{9}[4(d + \bar{d}) \pm (u + \bar{u})]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\sigma_{2H}^{\pi^+ \pm \pi^-} = \frac{5}{9}[( u + \bar{u}) \pm ( d + \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

The polarized distributions may be expressed in a similar fashion:

[math]\sigma_{\frac{1}{2}}[/math](Struck quark spin is [math]\parallel[/math] to Nucleon spin)	[math]\sigma_{\frac{3}{2}}[/math] (Struck quark spin is [math]\not\parallel[/math] to Nucleon spin)

[math]\frac{d^3 \sigma^h_{1/2}}{dxdQ^2 dz}\approx \Sigma_q e_q^2 q^{\parallel}(x,Q^2)D_q^h(z,Q^2)[/math]

[math]\frac{d^3 \sigma^h_{3/2}}{dxdQ^2 dz}\approx \Sigma_q e_q^2 q^{\not\parallel}(x,Q^2)D_q^h(z,Q^2)[/math]

[math]\frac{d^3 \sigma^h_{1/2(3/2)}}{dxdQ^2 dz}\approx \Sigma_q e_q^2 q^{+(-)}(x,Q^2)D_q^h(z,Q^2)[/math]

[math]\Delta \sigma_p^{\pi^+ \pm \pi^-} = \frac{1}{9}[4(\Delta u + \Delta \bar{u}) \pm (\Delta d + \Delta \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\Delta \sigma_n^{\pi^+ \pm \pi^-} = \frac{1}{9}[4(\Delta d + \Delta d^-) \pm (\Delta u + \Delta u^-)]D_u^{\pi^+ \pm \pi^-}[/math]

[math]\Delta \sigma_{2H}^{\pi^+ \pm \pi^-} = \frac{5}{9}[(\Delta u + \Delta \bar{u}) \pm (\Delta d + \Delta \bar{d})]D_u^{\pi^+ \pm \pi^-}[/math]

Delta d-over d

[math]X_{Bj}[/math] vs [math]\frac{\Delta d_v}{d_v}[/math]

PV asymmetry

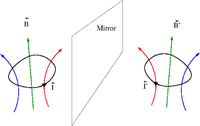
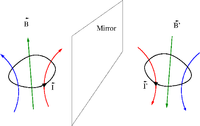
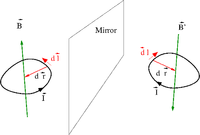
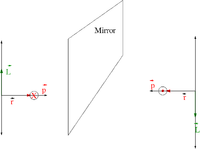
What is wrong with this picture

I look at the magnetic field of a current carrying wire in a mirror.

The B-field does not obey the right hand rule convention used to determine its direction based on the direct of the current

Here is the physically correct picture

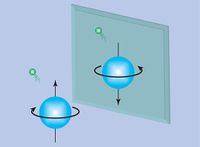
axial-vectors

An axial vector is the cross product of two polar vectors

[math]\vec{A} = \vec{V}_1 \times \vec{V}_2[/math]

The vector gains an additional sign under an improper transformation like reflection.

Improper transormation: When I raise my right hand in a mirror it looks like my left hand is up. Only 2 of the 3 axes flip direction (I still look upright).

Biot-Savart Law for finding magnetic field

[math] \vec{B} = \int\frac{\mu_0 I }{4\pi} \frac{d\vec{l} \times \vec{r}}{|r|^3},[/math]

Angular momentum

In physics we can ask if we observe the same number of electrons independent of the nucleus' spin.

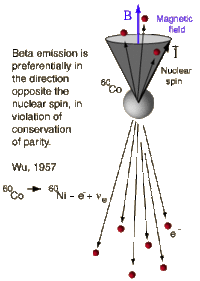
Wu's Co-60 Beta decay

A neutron in the Cobalt nucleus converts into a proton and emits an electron (charge conservation) leaving a Nickel nucleus.

[math]{60\atop 27 }Co_{33} \rightarrow {60\atop 28 }Ni_{34} + \beta + \bar{\nu}_e[/math]

The observation: The Co-60 nucleus can be polarized along an external B-field when cooled down to 0.01 K

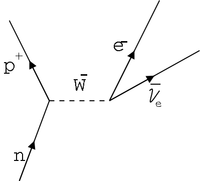
The decay is currently described being the result of a down quark in the neutron changing into an up quark and a negative W boson. The negative W boson decays into an electron and an anti-electron neutrino. Notice that charge, Baryon number, and Lepton number are conserved.

The W-boson has a mass of about 80 GeV but the mass of a neutron is about 1 GeV and Co-60 is only 60 a.m.u. \times (931.5 MeV/a.m.u) = 55 GeV .

How can you have a W-boson of mass 80 GeV in this decay?

Answer: Virtual particles.

Virtual Particles

You can "violate" conservation of energy by an amount \Delta E for an interval of time \Delta t given by the Heisenburg uncertainty principle such that

[math]\Delta t \le \frac{\hbar}{\Delta E}[/math]

Or if you prefer to think of an interaction Range (R) when the Z-boson is traveling at the speed of light then

[math]R = c \Delta t \lt \frac{c \hbar}{\Delta E} = \frac{200 \mbox{MeV} \cdot \mbox{fm} }{80 \mbox{GeV}} \sim 2 \times 10^{-3} \mbox{fm} = 2 \times 10^{-18} \mbox{m}[/math]

A Fermi = fm = size of a nucleon, so a virtual Z-boson interaction could take place within 1/100 the size of a nucleon.

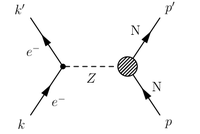
Z-bosons and the Weak Force

Z-boson is a neutral, spin 1 particle that mediates the weak force. It is its own antiparticle and has a mass of 91 GeV/c^2. Unlike the photon there isn't an E&M field which could induce a spin flip. The Z-boson is a "neutral" current which in this case transfers momentum.

[math]e^-\to e^- + Z^0[/math]

electrons can emit or absorb Z-bosons.

How does this happen when using JLab's < 6 GeV electron beam?

A measurement of d-Delta

The weak interaction is an axial vector interaction it is directly sensitive to the spin response of the proton during the [math]\Delta[/math] transition.

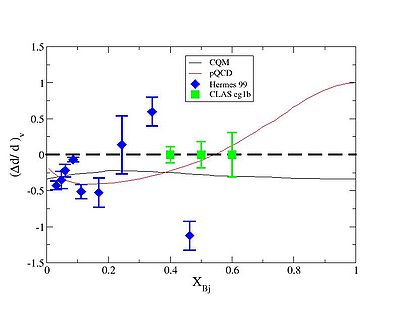
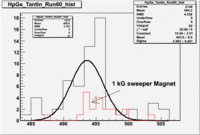
The figure below shows the statistical precision which can be achieved for a measurement of the low energy constant known as d_{Delta} using the current Qweak data set from Run I. The figure shows the expected inelastic PV asymmetry for several values of d_{Delta} as a function of Q^2. The low energy constant d_{Delta} characterizes the parity violating electric dipole matrix element for the [math]\gamma N \Delta[/math] transition accessible by inelastic parity violation measurements on the proton. The application of Siegert's theorem at the photon point, (Q^2=0), results in the Q^2 independence of the transition amplitudes leading term. The statistical precision of a 1 week long measurement, predicted using the current data set, is shown in the figure as well. In addition to measuring a fundamental low energy constant, the results may also have implications to hyperon decay physics as d_{Delta} impacts the asymmetry parameter in radiative hyperon decay physics such as the [math]\Sigma^+ \rightarrow p \gamma[/math] decay.

[math]A_{LR} = - \frac{G_F}{\sqrt{2}} \frac{Q^2}{4 \pi \alpha} \left [ \Delta^{\pi}_{(1)} + \Delta^{\pi}_{(2)} + \Delta^{\pi}_{(3)}\right ][/math]

[math] \Delta^{\pi}_{(1)}[/math][math] \Delta^{\pi}_{(2)}[/math][math] \Delta^{\pi}_{(3)}=2(1-4 \sin^2(\theta_W))(1+R^{\Delta}_A)F(Q,s)[/math]

[math]R^{\Delta}_A[/math]= electroweak radiative correction

[math]F(Q,s)[/math] = axial form factor

Student Projects

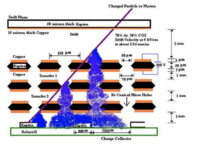
Detector Construction

Drift Chambers for Hall-b

GEM detectors

NaI detectors

Future

The dashed line represents a pQCD prediction while the solid line represents the prediction from a hyperfine perturbed constituent quark model. The solid triangles are measurements from X.~Zheng {\it et al.}, Phys.~Rev.~Lett.~92 (2004) 012004 and the diamonds are from Phys.Rev.D71:012003,2005. The squares represent a prediction of the precision obtained by a SIDIS measurement performed using and energy upgrade CEBAF and the upgraded CLAS. The risers represent systematic uncertainty and the error bar lines are statistical uncertainties.

Virtual particles

From DesY physicist Matt McIrvin (1994)

What are virtual particles?

One of the first steps in the development of quantum mechanics was Max Planck's idea that a harmonic oscillator (classically, anything that wiggles like a mass bobbing on the end of an ideal spring) cannot have just any energy. Its possible energies come in a discrete set of equally spaced levels. An electromagnetic field wiggles in the same way when it possesses waves. Applying quantum mechanics to this oscillator reveals that it must also have discrete, evenly spaced energy levels. These energy levels are what we usually identify as different numbers of photons. The higher the energy level of a vibrational mode, the more photons there are. In this way, an electromagnetic wave acts as if it were made of particles. The electromagnetic field is a quantum field.

Electromagnetic fields can do things other than vibration. For instance, the electric field produces an attractive or repulsive force between charged objects, which varies as the inverse square of distance. The force can change the momenta of the objects.

Can this be understood in terms of photons as well? It turns out that, in a sense, it can. We can say that the particles exchange "virtual photons" which carry the transferred momentum. Here is a picture (a "Feynman diagram") of the exchange of one virtual photon.

                    \                /
                     \   <- p       / 
                      >~~~         /          ^ time
                     /    ~~~~    /           |
                    /         ~~~<            |
                   /              \            ---> space
                  /                \

The lines on the left and right represent two charged particles, and the wavy line (jagged because of the limitations of ASCII) is a virtual photon, which transfers momentum from one to the other. The particle that emits the virtual photon loses momentum p in the recoil, and the other particle gets the momentum.

This is a seemingly tidy explanation. Forces don't happen because of any sort of action at a distance, they happen because of virtual particles that spew out of things and hit other things, knocking them around. However, this is misleading. Virtual particles are really not just like classical bullets.

How can they be responsible for attractive forces?

The most obvious problem with a simple, classical picture of virtual particles is that this sort of behavior can't possibly result in attractive forces. If I throw a ball at you, the recoil pushes me back; when you catch the ball, you are pushed away from me. How can this attract us to each other? The answer lies in Heisenberg's uncertainty principle.

Suppose that we are trying to calculate the probability (or, actually, the probability amplitude) that some amount of momentum, p, gets transferred between a couple of particles that are fairly well- localized. The uncertainty principle says that definite momentum is associated with a huge uncertainty in position. A virtual particle with momentum p corresponds to a plane wave filling all of space, with no definite position at all. It doesn't matter which way the momentum points; that just determines how the wavefronts are oriented. Since the wave is everywhere, the photon can be created by one particle and absorbed by the other, no matter where they are. If the momentum transferred by the wave points in the direction from the receiving particle to the emitting one, the effect is that of an attractive force.

The moral is that the lines in a Feynman diagram are not to be interpreted literally as the paths of classical particles. Usually, in fact, this interpretation applies to an even lesser extent than in my example, since in most Feynman diagrams the incoming and outgoing particles are not very well localized; they're supposed to be plane waves too.

The uncertainty principle opens up the possibility that a virtual photon could impart a momentum that corresponds to an attractive force as well as to a repulsive one. But you may well ask what makes the force repulsive for like charges and attractive for opposite charges! Does the virtual photon know what kind of particle it's going to hit?

It's hard even for particle physicists to see this using the Feynman diagram rules of QED, because they're usually formulated in a manner designed to answer a completely different question: that of the probability of particles in plane-wave states scattering off of each other at various angles. Here, though, we want to understand what nudges a couple of particles that are just sitting around some distance apart—to explain the experiment you may have done in high school, in which charged balls of aluminum foil repel each other when hanging from strings. We want to do this using virtual particles. It can be done.

In QED, as in quantum mechanics in general, there are wave functions with complex-number values which have to be squared to get probabilities. We want to see that the wave function changes so that the like charges, on average, are repelled from each other, and the unlike charges, on average, are attracted.

Suppose, for simplicity, that the charged particles' wave functions are initially Gaussians at rest, that is, normal bell-shaped, real-valued functions, and that they are lined up along the x axis. You can think of the wave functions, schematically, as looking like this:

             ____                         ____   
            /    \                       /    \     x ->  
          _/      \_                   _/      \_  
0 _______/          \_________________/          \__________

where you are supposed to imagine that those ASCII stairs are actually continuous, smooth curves. Imagine, furthermore, that the distance between the two lumps in this diagram is much larger than the width of a lump. If you know some quantum mechanics, you know that in the absence of any forces, the lumps will just spread out symmetrically (well, if the particles are identical we have to worry about other details when they start to overlap substantially, but if the lumps are far apart that won't happen for a while). If there is an overall constant potential energy, that will give the wave functions an additional rotating phase, but we can always ignore that without affecting any physical quantities.

Concentrate on one of the particles, say, the one to the left. As well as the ordinary wave functions that are functions of position, I can also define wave functions in "momentum space": there is a probability amplitude for every momentum, which you square to find the probability density. If its wave function in space is Gaussian, then the wave function in "momentum space" is also Gaussian: as a function of the x component of momentum it is also bell-shaped. The narrower the position-space Gaussian is, the wider the momentum-space Gaussian is; that is Heisenberg's uncertainty principle!

                       _____________
                    __/      ^      \__
                 __/         |         \__         p ->
            ____/            |            \____
 0 ________/           zero momentum           \____________

In order to make this problem tractable, I should specify that the momentum-space wave function isn't so wide (in other words, the position-space wave function isn't so narrow) that consequent relativistic effects become large. (For electrons, this doesn't happen until the position wave functions are squeezed into a space much smaller than an atom; and if the particle is more massive you have to squeeze it even more.) Also, I will ignore the particles' magnetic moments, if they have them, because all I care about is the electrostatic force.

Now, consider a virtual photon that comes from the particle on the right and is absorbed by the particle on the left. Actually calculating the photon's wave function is a little hairy; I have to consider the possibility that the photon was emitted by the other particle at any prior time. (However, I can save myself a little effort later by automatically including the possibility that the photon actually comes from the particle on the left and is absorbed by the particle on the right, with the recoil nudging the left particle: all I have to do is include situations in which the photon is "emitted on the right" in the future and goes "backward in time," and take its momentum to be minus what it really is! As long as I remember what's really going on, this trick is formally OK and saves a lot of trouble; it was introduced by Richard Feynman.)

When I include all of these possibilities, it turns out that I can approximate the photon's momentum-space wave function usably well by the following: the wave function is a function proportional to the electric charge of the emitting particle (in a sense this defines what electric charge is), and it has a few big, narrow spikes in it. One spike is proportional to -i times the charge, and is to the left of the origin; the other spike is minus that and is to the right of the origin. (There is also a third spike at zero momentum that has a real amplitude, but it turns out not to do anything important at the end of the day—it provides a constant potential energy—so I'll ignore it.) The imaginary component of the photon wave function looks like this, if the emitting particle was a negatively charged electron:

                |
 +i             |     zero momentum                p -->
                |          |
                |          v
  0 ____________|________________________________________
                                     |
                                     |
                                     |
  -i                                 |
                                     |

If the emitting particle was positively charged, this picture is upside down.

(A note for experts only: The somewhat QED-savvy may be puzzled by the total nonresemblance of this to any well-known photon propagator. That's because I'm not going into momentum space in every direction, just in the x direction. The more QED-savvy will notice that I am making some pretty monstrous oversimplifications here. Actually they are not so bad; what I'm doing is the equivalent of assuming that the potential can be locally approximated by a sinusoid! If the wave packet is small enough in position space, a Coulomb potential and a sinusoidal one are both effectively a constant-force potential, so I can do this. Neglecting all magnetic effects and taking the nonrelativistic limit, the amplitude for transfer of a given momentum by a single virtual photon—which is essentially what I am colorfully, and without much prevarication, labeling the "photon's momentum-space wave function"— has to have an imaginary part odd in p_x because the potential is real, so in any case the qualitative effect will be the same as what I describe below, and for essentially the same reasons. It's just so much easier to convolute spikes. As for the single-particle "wave functions" of the charged particles, I can speak of them with fair correctness because the particles are far apart and slowly moving.)

The effect of a virtual photon hit on the charged particle's momentum-space wave function is, then, quite simple. The photon has a certain probability amplitude of knocking the charged particle to the left and a certain amplitude of knocking it to the right. The probability amplitude for each possibility is just proportional to i times the charge of the particle times the photon wave function times the time! (The other constants of proportionality depend on the system of units; we're not being terribly quantitative so don't worry about them.) We multiply the original charged particle's wave function—shifted to the right or left in momentum space, depending on which way it got knocked by the photon—times this amplitude, for each of the two possibilities, and then add the modified wave functions for the two possibilities together.

If both particles are negatively charged, or both are positively charged, then we're adding a right-side-up wave function, shifted to the left, to an upside-down wave function shifted to the right. The result is real-valued and looks something like this:

                _____
 +            _/     \_ zero momentum
           __/         \   |                      p -->
        __/             \  |
 0  ___/                 \ v 
                          \                   ________
                           \               __/
                            \           __/
 -                           \_       _/
                               \_____/

and it increases in size as time goes on, from zero at the start of the problem. If the particles have opposite charges, then you should flip that picture upside down. The result is proportional to the product of the two charges, because we multiplied in the other particle's charge when finding the photon wave function, and this particle's charge when the interaction happened.

Now, by now you might be a little disturbed. We get wave functions by squaring amplitudes. The lump to the right of the origin goes down just as far as the lump to the left goes up. So isn't the probability that the photon knocked the particle's momentum toward the other one just as large as the probability that it knocked it away? No, because there is still some probability amplitude that no photon interaction occurred at all, and since we have no way of unambiguously telling one possibility from the other, we need to add the two wave functions together before squaring them! (There are also amplitudes for larger numbers of interactions, but for short times, we need not worry about those. Also, the "no-hit" wave function is not exactly the unmodified one, because of its own natural time evolution, but for short times all that does to the momentum-space wave function is give it a small imaginary part that we don't care about here.)

I said the unmodified wave function was positive, so the post-hit wave function will interfere with it constructively on the left side of the origin, and destructively on the right (or vice versa if the particles have opposite charges). So after a little time has passed, the wave function looks something like this in momentum space:

           ________    zero momentum
         _/        \___    |
        /              \__ v                  p -->
      _/                  \__
    _/                       \______
 0 /                                \________________

Squaring the wave function gives you a probability distribution whose hump is also shifted to the left. The momentum of the particle is skewed leftward—it is being repelled from the other particle! If the charges have the same sign, the interference goes the other way and the particle's momentum is skewed rightward, for a net attraction. The position-space wave function itself will tend to move leftward or rightward as it spreads out, as the case may be.

You might wonder: What happens when the time gets late enough that the negative hump in the struck wave function more than cancels the original wave function? Well, at those times, my analysis here is not enough, because there is also a significant amplitude that two photons have hit the particle (and things get gnarlier, because they could have hit it in any order); for still longer times I need to consider three, and so on.

The important point is that the photon doesn't "know" that it's going to hit a particle of the same charge as the one that emitted it, or of the opposite charge. The distinction between attraction and repulsion actually arises when the effect of the virtual photon interferes with the unperturbed wave function! In general, the distinction comes from interference between the contributions from odd and even numbers of virtual photons traveling from one particle to the other. Each such photon multiplies a factor of the product of the two charges into its contribution to the wave function; so the odd processes will get a factor of −1 from this product (times other things, of course) if the charges are different and +1 if they are alike, whereas the even processes get a factor of +1 in either case. The interference between "odd" and "even" terms in the wave function yields effects which survive even upon squaring the amplitude to get a probability. In the discussion above, by limiting consideration to short times, I've been able to ignore everything but the no-photon and one-photon processes.

This interference, with the amplitude for photon collision increasing smoothly with time, is also part of the reason why you can regard a stately and continuous thing like the evolution of a wave packet as the result of violent particle-collision events. As discordant as these phenomena may seem, they are actually two sides of the same coin. In the classical realm we don't see the spreading of the wave functions, but we do see this gradual net change in momentum, and it is what we call a force.

Do they violate energy conservation?

We are really using the quantum-mechanical approximation method known as perturbation theory. In perturbation theory, systems can go through intermediate "virtual states" that normally have energies different from that of the initial and final states. This is because of another uncertainty principle, which relates time and energy.

In the pictured example, we consider an intermediate state with a virtual photon in it. It isn't classically possible for a charged particle to just emit a photon and remain unchanged (except for recoil) itself. The state with the photon in it has too much energy, assuming conservation of momentum. However, since the intermediate state lasts only a short time, the state's energy becomes uncertain, and it can actually have the same energy as the initial and final states. This allows the system to pass through this state with some probability without violating energy conservation.

Some descriptions of this phenomenon instead say that the energy of the system becomes uncertain for a short period of time, that energy is somehow "borrowed" for a brief interval. This is just another way of talking about the same mathematics. However, it obscures the fact that all this talk of virtual states is just an approximation to quantum mechanics, in which energy is conserved at all times. The way I've described it also corresponds to the usual way of talking about Feynman diagrams, in which energy is conserved, but virtual particles can carry amounts of energy not normally allowed by the laws of motion.

TF_ResearchInterests