Se170063 Pure Se Wide Gauss Window Expansion
In this example I only weighted the histogram by the mass of the sample, which in the case of the pure selenium sample is 0.0971g.
| 400 <t< 640 sec | 1100 < t < 1360 sec | 1875 < t < 2150 | 2650 < t < 2930 sec | 3400 < t < 3690 sec | 4120 < t < 4400 sec | 4840 < t < 5130 sec | |
| Original Window Counts | 564700 | 536100 | 497100 | 432200 | 380500 | 319900 | 289400 |
| Original Window Background (Integrated) | 85711 | 86719 | 78500.2 | 73399.5 | 76327.6 | 61106.5 | 57459.7 |
| Original Window Difference | 478989 | 449381 | 418599.8 | 358800.5 | 304172.4 | 243572.4 | 231940.3 |
| Expanded Window Counts | 587300 | 558100 | 517500 | 451400 | 398700 | 336000 | 304500 |
| Expanded Window Background | 108563 | 108152 | 98915.2 | 92183.5 | 93245 | 77423.5 | 72660.2 |
| Expanded Window Difference | 478737 | 449948 | 418584.8 | 359216.5 | 305455 | 258576.5 | 231839.8 |
| Error in counts | 252* | 567 | 15* | 416 | 1282.6 | 15004.1 | 100.5 * |
| .dat file entry | 7.598793988 +/- 0.0005261081152 | 7.454944728 +/- 0.0012617356 | 7.327899514 +/- 0.0000358337 | 7.1557322 +/- 0.0011594187 | 6.955469002 +/- 0.0042166876 | 6.768379905 +/- 0.0616001649 | 6.684354367 +/- 0.0004333011 |
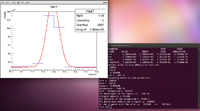
Using this method there seemed to be a problem with the background. When finding the error in the counts, sometimes the value was negative. Below is the example of the last timed run where 4840 < t < 5130
Here you can see that the total number of counts in the window is 289400, while the integral of the background, which is found in the terminal is 57459.7. So we have a difference of 231940.3 counts. The expanded window is shown below.
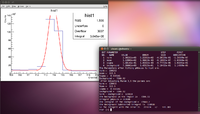
Now here it is shown that the total number of counts within the window is 304500 counts, while on the terminal we can see that the integral of the background is 72660.2 counts, which gives a difference of 231839.8 counts. Subtracting these two numbers to find the error in the number of counts, we find that
This result is slightly troubling, but it did not occur in the ash + se sample at all. It seems that the macro may be overcompensating for the background.
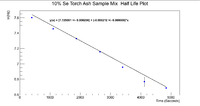
Below is a plot of the activity vs. time to get the half life and initial activity
The root window gives a slope of -0.000211997 +/- 1.3423e^-7. This gives us a half life of
54.49 +/- 0.03 Minutes
We can find the initial activity by using the constant value given, which is 7.72506 +/- 0.000255985.
Now we can correct for the efficiency, which will be the same factor as the mixed (which should cancel)
while the error is
Now we must trace this signal back to t = 0 for the mixture (since that is what it will be compared to). The mixture was measured 400 seconds prior to the pure sample, which gives
while the error is