Se170063 Nickel Investigation

In finding the initial activity of the front nickel foil of this sample, look at the window from [1356,1368]. The method I used here was simply finding the number of counts within this window and subtracting the integral of the constant found by the fit. Below is a picture of the line of interest.

Note that this spectrum is weighted by the inverse of the mass of the nickel. So the natural log of the activity is what we want to put in the .dat file to feed into root. Below is the math that I did to find these numbers

[math] N = N_{total} - \int_{1356}^{1368} C dE [/math]

After the number of counts have been found, I used the following formula for the error

[math] \sigma_N = \sqrt{N} [/math]

So now we have the number of counts for the line of interest and its associated error, so we must convert this into an activity, correct for the efficiency, and take the natural log.

[math] A_t = \frac{N_t}{t} [/math]

[math] \sigma_{A_t} = \frac{\sigma_{N}}{t} [/math]

[math] A'_t = \frac{A_t}{\epsilon} [/math]

[math] \sigma_{A'_t} = \frac{\sigma_{A_t}}{\epsilon} [/math]

Now we can simply take the natural log of the efficiency corrected activity. To find the error after taking the natural log, use

[math] \sigma_{\ln{A'_t}} = \frac{\sigma_{A'_t}}{A'_t} [/math]

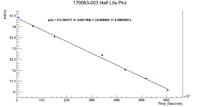
Below is the plot for the activity and half life of the nickel foil

Using the slope of this graph, we can find that the half life is

[math] t_{\frac{1}{2}} = \frac{\ln{2}}{\lambda} = 35.71 hours [/math]

[math] \sigma_{t_{\frac{1}{2}}} = \frac{\ln{2}*\sigma_{lambda}}{\lambda^2} = 0.04 hours[/math]

This does capture the accepted half life of Ni-57 in 2 standard deviations, which is a good sign.

Using the method below and doing a time correction backward 5280 seconds to coincide with the first selenium mixture measurement, we find the activity of the nickel is

[math] A_0 = 1835578.669 \pm 3268.41 \rightarrow 49.61 \pm 0.88 \mu Ci[/math]