Randy Spaulding
A Neutron Detector Array
Final Version (9/18/2009): File:RJS Thesis.pdf
Signature page: File:RandySpaulding Thesis SigPage.pdf
Original submitted version: File:SpauldingThesis2009 V1.pdf
Abstract
Helium-3 gas has long been a popular medium for neutron detection because of its enormous 5320 barn thermal cross-section. Unfortunately, helium-3 is not found in significant naturally-occurring quantities on Earth. The existing supply of helium-3 is essentially exclusively limited to the radioactive decay of tritium stockpiles. Increasing competition over the world’s finite helium-3 reserves creates an urgent need to utilize the gas in the most efficient manner possible. A new concept for neutron detector design using an array of low-pressure helium-3 drift tubes nestled inside a polyethylene lattice has been developed at Los Alamos National Laboratory (LANL). This detector design promises to be 2.5 to 3.5 times more efficient than previous systems using high-pressure helium-3 tubes. A prototype detector containing 72 helium-3 tubes was constructed at LANL for benchmarking purposes as well as supporting standoff interrogation experiments. This thesis reports the results of several benchmarking tests to compare the detectors performance with the predictions of the Monte-Carlo program MCNPX. A semi-deterministic method for calculating detector responses to environmental neutron scattering, called efficacy, is used to quantify the performance of the new detector concept. The goal of this thesis is to illustrate a detector design concept which minimizes the use of helium-3.
Chapter 1 Introduction
1.1 History of the Neutron
The discovery of the neutron is credited to J. Chadwick in 1932. Chadwick was following up on an observation made by I. Curie-Joliot and F. Joliot in 1931; in 1930, Bothe and Becker had first produced radiation that they assumed consisted of “very penetrating gamma rays” by bombarding light elements such as boron and beryllium with polonium alpha rays. Curie-Joliot and Joliot placed sheets of paraffin in the path of this yet-unknown radiation, which produced radiation that behaved like energetic protons. The photon energy they calculated to produce these assumed protons through a process similar to the Compton effect was an unrealistic 55 MeV. Chadwick confirmed that these were indeed protons and postulated that they were being produced by massive, energetic particles having a neutral electric charge instead of photons. The lack of electric charge of these “neutrons” explained their ability to penetrate matter with little absorption [1]. Unfortunately, the lack of electric charge also makes it impossible to measure the mass of the neutron using a conventional mass spectrometer. It was not until two years later in 1934 that Chadwick and Goldhaber were able to first measure the mass of the neutron by splitting deuterons with Thorium gamma-rays [2]. The neutron rest mass, now commonly used as a physical mass reference constant , is . 1.2 Neutron Detection The very long interaction length resulting from the zero net electric charge of the neutron also makes it very difficult to detect them directly. However, neutrons do have a significant cross-section for many nuclear interactions such as elastic scattering, inelastic scattering, (n, γ), (n, p), (n, n’), (n, fission) etc. Neutrons are easily detected via interactions of the secondary charged particles produced during one of the preceding nuclear reactions.
1.2.1 Some examples of neutron detectors
The reaction products are detected either in real time via direct charge conversion, or offline, by activation of a sample and monitoring of its radioactive decay [4]. Charge-conversion methods are predominant in most nuclear experiments because they give immediate or near-immediate results, while activation techniques [3] remain popular for small-scale experiments, high-radiation environments, and applications where the neutron spectrum needs to be known, such as boron-neutron capture therapy (BNCT) [6]. This document will focus on a handful of the real-time techniques that offer the highest practical detection efficiencies for epithermal neutrons; see reference [4] for a more complete discussion.
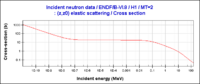
Figure 1: Cross section versus neutron energy for several common neutron-detection processes [4]
Figure 1 shows the cross-section for several of the most common reactions used in neutron detection. The strong energy dependence shown by these examples is characteristic of all neutron interactions. As a result, the scientist typically has a large degree of freedom in choosing the detector that is most suited to the energy range of neutrons present in his or her experiment. Reactions whose cross-sections dominate at low neutron energies can be used effectively for detecting high-energy neutrons by adding moderating material around the detector. The moderating material slows the neutrons down through multiple scattering events. The energy lost by the neutron in scattering from a nucleus of mass is readily calculated from kinematics:
(1.1) [8] where is the initial energy of the incident neutron, is the final energy, and is the scattering angle in the center-of-mass frame. The relationship between energy loss and mass of the nucleus is more apparent when this equation is rewritten in a different form:
(1.2)
which clearly shows that the energy transfer decreases as as atomic mass increases. Thus, light nuclei, in particular hydrogen, make the most effective neutron moderators, as they remove a greater fraction of the incident neutron’s momentum per collision. This form also shows that maximum energy loss occurs at θ = π (pure backscattering) and no energy transfer occurs for θ = 0 (no collision). The most popular moderating material is polyethylene ((CH2)n), or PE. PE has density similar to water (~0.89-0.97 g/cm3) and high hydrogen content (14% by mass). PE is substantial enough to be an effective moderator while being less bulky than heavy metals and easier to handle in the laboratory than water or liquid hydrogen. It is also inexpensive to produce and machine. The density of polyethylene increases as the average length of the ethylene chains grows. Polyethylene sold commercially is sorted by chain length and categorized by density. High-density polyethylene (HDPE) obtained in such fashion typically has a guaranteed average density of 0.93-0.95 g/cm3.
1.2.1.1 Scintillator-based neutron detectors
A scintillator is a material that fluoresces when bombarded with ionizing radiation. Many materials scintillate, including various aromatic liquids, amorphous solids such as plastics and glasses, and inorganic crystals such as NaI and CsI. All of these materials detect ionizing radiation in the same fashion; the total optical energy produced is directly related to the energy transferred to the scintillator. The optical photons are then collected and converted into an electrical signal by a photomultiplier tube (PMT). Organic and other hydrogenous scintillators are inherently sensitive to neutrons because of the large cross-section of the n-p elastic scattering reaction (denoted H1(n, n)H1 in Figure 1). These are called proton recoil detectors. See Figure 2. Other scintillators are combined with a neutron-sensitive material such as gadolinium, boron-10, or lithium-6, which all have large cross-sections for thermal neutrons . These are referred to as doped scintillator detectors. Neutron detection with scintillators is a highly-efficient process. However, scintillator detectors are also very sensitive to all other forms of ionizing radiation, and thus any incident flux of gammas, betas, etc. creates a large background. The inclusion of high-Z shielding materials around the detector can reduce the background, as the neutrons easily penetrate such materials but gammas and betas are absorbed. Additionally, in some cases the neutron signals can be separated from the gammas and betas by pulse-shape discrimination techniques. Efficiencies in the epithermal and fast regimes (En >~1 keV) are on the order of 30-50% [9] . Efficiencies in the thermal regime for doped scintillators can effectively reach 100% [11, 12].
Figure 2: Organic scintillation detectors detect fast neutrons via proton recoil.
1.2.1.2 Helium-3
Helium-3 is a monatomic gas having density 0.134 x 10-3 g/cm3 at standard temperature and pressure (STP). The He-3(n, p)t reaction has a cross-section of 5320 barns [13] for thermal neutrons--fourth-greatest among the stable nuclides behind only Gd-157 (2.54 x 105 bn), Gd-155 (6.09 x 104 bn), and Eu-151 (9.2 x 103 bn) [14]. The large cross-section and modest energies of the daughter particles make He-3 an ideal candidate for use in gaseous detectors. The helium-3 gas is typically mixed with a proportional gas and possibly also a quench gas to improve signal-to-noise and stabilize the Townsend avalanche. Historically, detectors have been typically operated at a pressure of 2-10 bar to maximize neutron detection efficiency. However, this practice is very wasteful of the He-3 gas because of decreasing returns in efficiency as pressure is increased (see Figure 12 on page 25). There is a significant ongoing effort at Los Alamos National Laboratory (LANL) studying the use of atmospheric-pressure tubes containing a few hundred mbar of helium-3 in hopes of reducing this wastefulness on a widespread scale .
Figure 3: The 3He(n,p)t reaction for thermal neutrons
Figure 4: Energy spectrum of 2”-dia. x 48"-long detector containing 200-mbar He-3 and 800-mbar proportional gas. Neutron counts appear above 191-keV and background counts from gamma-rays, cosmic rays, and electronic noise appear at lower energies, as indicated. Wall effects from both p (573 keV) and T (191 keV) daughters are clearly resolved [15].
Figure 4 shows an energy spectrum from an atmospheric-pressure detector containing a mixture of He-3 and proportional gas. The proportional gas produces a sharp full-energy peak having a full-width-at-half-maximum (FWHM) ~5% [15]. The low-energy background peak is produced by electronic noise, gamma-rays, and cosmic-ray muons and is typical of all gaseous detectors. The two “shelves” at 191-keV and 573-keV are produced when one of the energetic daughter particles (proton or triton, respectively) intersects the wall of the tube and does not deposit its entire energy in the gas. These shelves are referred to as wall effects. The energetic proton from the He-3 reaction has a range of ~1.5 cm in atmospheric-pressure tubes, while the triton’s range is ~0.5 cm. These wall effects, which are present in all gaseous neutron detectors, cause a minor loss in counting efficiency, as counts that do not contribute to the full-energy peak could be lost in the noise/cosmic-ray background peak that appears at low energies. This is not a great concern for a fairly new tube, as the wall effects represent a small fraction of the total counts and the background is easily discriminated out. However, the noise level tends to increase as the tube ages because of effects such as gas spoiling, or gradual replacement of the proportional gas with air by leakage and diffusion through the wall of the tube. Gas spoiling also causes wall effects to increase slightly because the air is less dense and has less stopping power than the proportional gas. Consequently, the range of the charged particles increases as proportional gas is lost. Researchers at LANL are currently developing techniques that will be applicable to all gaseous proportional counters, to monitor the health of the tube and predict its remaining lifetime [15].
1.2.1.3 Boron-10
Boron-10 is another popular medium for thermal neutron detection due to its high cross-section (3845 bn [13]) and high Q-value (see Figure 5). As depicted in the figure, the B-10(n,α)Li-7 reaction can populate either the ground state of the Li-7 ion or the first excited state. In the latter case, the excited Li-7 nucleus immediately decays to ground , emitting a 477-keV gamma ray. Boron-10 is only 19.9% abundant in natural boron, the remainder being Boron-11. For this reason, it is typical to use isotopically-enriched boron-10 in neutron counters.
Figure 5: Thermal neutron capture on Boron-10
Boron is used for neutron detection in several schemes involving both solid and gaseous forms [4]. The most common form used is gaseous boron triflouride (BF3). BF3 used for this purpose is typical enriched in B-10 to near 100%. At STP, (B-10)F3 has a density of 2.99 x 10-3 g/cm3 at STP at and contains 14.9% B-10 by mass. The sensitivity of gaseous BF3-filled detectors is somewhat lower than that of He-3. However, Stokes, Meal, and Myers showed that BF3 detectors are particularly radiation-resistant and can be operated in gamma fluxes of 1000 R/hr or more [17], making them attractive for mixed-waste and reactor applications.
1.2.2 Detector Efficiency
The concept relating the measured count rate in an experiment to the current of interacting incident particles present is called efficiency . There are several methods of defining detection efficiency; the terminology used in this document for the most common definitions will be: a) conversion efficiency, b) intrinsic efficiency, and c) total efficiency. Another quantity commonly used by commercial detector manufacturers is sensitivity, which is defined as counts per second per unit incident particle flux. Many of these quantities involve assumptions about the energy and/or angular distribution of the incident particles, as will be explained in following sections. Conversion efficiency refers to the ability of a detection system to convert the energy from a reaction into recordable signals, and is defined by:
Conversion efficiency is thus the probability of obtaining a useful signal each time the desired reaction occurs. Written another way, conversion efficiency equals unity less losses to various processes:
Conversion efficiency plays a fundamental role in determining the count rate from a nuclear experiment. In general, the contribution to the count rate dC in a volumetric detector for particles having energy between E and E + dE in the volume element dV is the reaction rate dR times the conversion efficiency, or:
(1.3) [4]
(1.4)
where = number of target atoms per unit volume
(E) = reaction cross-section at energy E
= flux per unit energy interval, defined as
(1.5) [7] where = number density, the number of particles of interest per unit volume, and is the velocity of the particles. In practice, determination of the conversion efficiency can be quite complicated, as most physical detectors employ multiple energy conversion schemes to produce the final signal and many of the reactions themselves involve multiple chains, e.g. B-10 (n, α) {Li-7, Li-7*}. Thus, experimenters frequently neglect direct determination of the conversion efficiency. However, it should not be neglected when monte-carlo particle transport codes such as MCNPX are used, as these codes typically only estimate the reaction rate—not the actual count rate in the detector. In many cases, the losses are small and can be assumed to be equal to or near unity over the entire applicable energy range. The detectors described in this document generally all fit this requirement.
Figure 6: Detection of particles in a nuclear physics experiment
The total efficiency, , and the intrinsic efficiency, , are inherently related quantities describing the count rate for a particular experimental configuration. Total efficiency is defined as counts per particle emitted from the source, while intrinsic efficiency is defined as counts per particle crossing the detector boundary. In the broadest sense, the relationship between the two involves the angular emission characteristics of the source; the geometry of the experiment, including the physical sizes and placement of source and detector; and the presence of scattering materials in the flight path of the particle and the environment:
(1.6)
where I is the source emission rate of particles originating from the point , having energy E, into the cone ; , the intrinsic efficiency, is the fraction of particles having energy , crossing the point (x, y, z) on the detector’s surface, at the angles of incidence θ and φ, that create useful signals in the detector; and is the transfer function that envelops all interactions experienced by every source particle during its flight from the source to the detector (see Figure 6). The transfer function accounts for attenuation and up- or down-scattering during transmission; environmental effects such as off-angle particles scattered toward the detector; secondary particle production; etc. In this form, the integral in the numerator is over the source volume, all source angles, and the detector surface area. The integral in the denominator is over the source volume and all source angles. The latter integral is written out explicitly to emphasize that, in order to achieve the proper normalization of “per source particle” one must normalize to the total source activity. Note that , the magnitude of the scattering function, can be >1, particularly for showers created by high-energy particles, representing multiplication of the source particles by reactions such as (n, xn). Equation (1.6) represents the formal relationship between and . In practice, nearly all nuclear physics experiments employ a general strategy of reducing the effects of finite source size and scattering objects, both in-flight-path and environmental, to negligible levels or eliminating them entirely. When this is true, the above expression can be greatly simplified to the form:
(1.7)
or alternatively, for small solid angles:
(1.8)
where is the solid angle of the volume source subtended by the detector, A is the surface area of the detector, and R is the distance to the source. As shown by Eq.(1.8), if the detector is small relative to the square of the source distance, the fractional solid angle is well approximated by the ratio of the projected area of the detector to the surface area of a sphere having radius R. This assumption goes hand-in-hand with one of the assumptions used in writing Eq.(1.7), that angular effects at the detector surface are negligible. In practice, efficiency is further simplified by averaging the convolution of the detector’s efficiency and the energy spectrum of the source over the applicable energy range, so that the efficiency can be conveniently quoted by a single number :
(1.9)
1.2.3 Note on calibration using check sources
The experimenter often desires to measure detector efficiency directly by means of a calibrated standard source. For fast neutron measurements with filled-gas-tube detectors such as He-3 and B-10, all information about the source neutron’s energy is usually lost before detection. As a direct result, it is only possible to measure the flux-convoluted average efficiency as in Eq. (1.9). When doing so, the experimenter must keep in mind that the energy spectrum of the neutrons present in the experiment can be, and generally is, quite different from that of the source used in the calibration. A nonuniform detector response over the applicable energy range can result in the experimental efficiency being different from the calibrated efficiency. This is typically the case for gas-tube detectors. See Figure 56 on page 102 for some examples of energy-efficiency curves. Depending on the application, it may sufficient to simply make note of awareness of this situation. However, for applications that require precise knowledge of the efficiency, it is crucial to quantify this effect by introducing a source-correction factor:
(1.10)
where is the experimental neutron energy spectrum and is that of the source. The square brackets in Eq. (1.10) denote that the energy spectra are required to have the same normalization—both are typically normalized to unity. Determination of and subsequently, , is commonly performed by Monte-Carlo computer simulations. Some example calculations comparing several neutron energy spectra to a Cf-252 standard are presented in Table 1. These calculations do not assume to be representative of all situations an experimenter will encounter in the laboratory; they merely demonstrate that can easily vary over a wide range that spans at minimum [18]. Source Description Source Correction Factor, γ (all ±5%) Cf-252 1.00 238U (nepithermal, fission) 0.560 AmBe 0.958 800-MeV protons on 238U target (Room return) 1.720 800-MeV protons on 238U target (delayed neutrons) 1.444 Table 1: Typical source correction factor values from LANL experiments
In Table 1, the 238U epithermal fission spectrum is presented for comparison purposes only. The two values from 800-MeV protons are taken from different periods of time within the same experimental setup. The “room return” value represents and the “delayed neutron” value was taken from . The 20% difference between the two demonstrates the added complexity of source correction effects in active interrogation experiments. Obviously, great care must be taken when calculating neutron yields from such experiments.
1.3 Motivation for this work
The goals of traditional portal monitoring systems are to monitor and control the movement of specific items throughout the country, and on a larger scale, worldwide. In this modern era of heightened terrorist activity, systems such as these have become pivotal in keeping the world’s people, governments, and economies safe and providing peace of mind for the general public. Of particular interest is the possible threat of a nuclear attack on United States soil. Prevention of such an attack requires (1) the detection of the Special Nuclear Material (SNM) in a safe and effective manner and (2) interception and neutralization of the material before it Figure 7: The Department of Homeland Security (DHS) employs multiple levels of detection and interdiction to thwart terrorist attacks in the United States [28] reaches the primary target and before it can be released on a secondary target. The difficulty in the detection stage is that while nuclear materials emit unique and known radiation signatures, these signals are fairly weak and easily shielded from radiation detectors. An additional problem is the enormous scale of the task. Any comprehensive solution must therefore offer maximum efficiency at minimal cost and must also provide sufficient flexibility and scalability for deployment in a wide variety of portal monitoring scenarios.
1.3.1 Active interrogation
Existing passive-interrogation methods are assumed to be largely ineffective at interdicting smuggled fissionable materials, particularly on national and worldwide scales [29]. Ironically, the difficulty in this task arises in part from the success of the existing safeguards that make it extremely difficult for terrorist organizations to obtain dangerous quantity of SNM. Terrorists having possession of a large amount of nuclear material would certainly go to extreme lengths to protect it [30]. The solution to the weak radiation signature emitted by SNM is to use an active probe—an energetic beam of particles. Active techniques include x-ray imaging and signal enhancement through induced nuclear fissions in the target. The latter technique can employ neutrons, bremsstrahlung photons from high-energy electrons, or protons to produce signatures unique to SNM in the form of beta-delayed fission neutrons [31, 32, 33]. These signatures can also be used to identify the species of the nuclear material [34], which can aid in determining the threat level.
Figure 8: Mammoth cargo container ships, or "boxships" carry millions of containers across the world's oceans annually.
One of the greatest conceived threats is the smuggling of a nuclear device via ocean-going vessel [35]. Millions of containers per year enter the USA by cargo container ship, bound to destinations nationwide [36]. The largest existing cargo container ships are capable of carrying over 15,000 8’x8’x20’ boxes. The danger is that these container ships provide a way for the terrorists to defeat land-based interdiction by detonating the device in or around the seaport of a major city. An additional potential threat is a nuclear device being delivered to a neighboring country and transported to the U.S. shore on a smaller vessel such as a private yacht. Researchers at LANL are currently investigating means of interrogating these vessels at a safe distance from shore. This technique is referred to as standoff interrogation.
1.3.2 Standoff interrogation
Standoff interrogation involves long-range active scanning with a source-to-target distance ranging from 100 m to perhaps 1 km or more . Ideally, the beam spot would be small enough for surgical scans--perhaps several feet in diameter at the target distance. Furthermore, the beam needs to be capable of penetrating several feet of dense material in order for scanning of boxships to be practical. The most viable candidate that meets all of these criteria is a beam of protons in the kinetic energy range 800 MeV < T < 4 GeV . A high-energy proton beam is readily produced with sufficient current and a small enough beam profile to perform the scan at such distances. It is extremely difficult to meet all of the above criteria with bremsstrahlung and neutron beams; the range of low- to medium-energy photons is limited by absorption in air and a neutron beam would require an impractical amount of high-energy flux. A high-energy photon beam could potentially satisfy all of the requirements to accomplish the scan, but it would not be less expensive to produce than a proton beam and it would be more difficult to meet radiological requirements because photons are much more penetrating than protons. The dose delivered by the proton beam potentially poses a significant radiological risk to crewmembers on the ship and/or illegal immigrants who may be stowed aboard the ship. This imposes a limit on the amount of beam current that can be used, and hence the available signal. Thus, maximization of neutron detection capability is crucial to this technique. Helium-3 is the most attractive medium from a detection standpoint due to its superior efficiency compared to B-10 and lesser sensitivity to photon and charged-particle backgrounds compared to plastic scintillators. Unfortunately, He-3 is fairly expensive because it is quite rare on Earth. Additionally, competing demands for He-3 such as proposed power generation via nuclear fusion threaten to make it difficult to obtain large quantities in the years to come. Combining these factors it becomes immediately apparent that there is a substantial cost factor associated with deploying He-3 detectors on any kind of national scale.
1.3.3 Fusion power and the worldwide He-3 shortage
The He-3 fusion reaction has been under extensive study for over 20 years and is now widely regarded to be one of the best long-term solutions to the world’s energy crisis. Reactor engineering and development aside, the overwhelming problem is that we simply do not have enough helium-3. Early studies estimated that tens of metric tons of He-3 would be required per year to supply the USA’s electricity demands. However, current worldwide He-3 production, being almost entirely limited to radioactive decay of tritium collected from spent nuclear fuel, is only in the tens of kilograms per year [39, 40, 41] —1000 times less than what is required to provide a viable fuel. Moreover, the quantity of He-3 required to build a research reactor would essentially exhaust the entire present worldwide stockpile [40]. The solution to this problem is beyond the scope of this work; however, its implication to the Homeland Security effort is clear: He-3 use must be minimized by identifying and implementing the most efficient use of He-3 on the basis of the quantity used.
Figure 10: The d-He3 fusion reaction
Figure 11: Virtually all helium-3 in present worldwide stores has been produced as a product of tritium β-decay.
1.4 Maximizing the efficiency cost factor for He-3 tubes Historically, use of He-3 drift tubes in the laboratory has been governed by the mantra “maximum efficiency in minimum space.” This has driven manufacturers to produce tubes containing as much as 40 atm He-3 [42]. Unfortunately, such high pressures result in very inefficient use of the He-3 gas due to processes such as self-shielding and increased background stemming from increased n-3He elastic scattering and increased sensitivity to gamma-rays and charged particles.
Figure 12: Efficiency of a 1" x 12" cylindrical He-3 detector versus He-3 partial pressure predicted by MCNPX. The straight line represents proportionality. At low pressures the tube is filled to 1 bar with a proportional gas consisting of Argon, CF4, and ethane (C2H6). The slope of the curve is greater than unity at very low pressures due to improved moderation provided by the fill gas itself.
Figure 13: The results of Figure 12 recast in terms of cost efficiency. The efficiency figure-of-merit (FOM) used in cost efficiency is defined as weighted efficiency per unit He-3 gas. The exponential weighting factor m controls the relative emphasis between efficiency and amount of gas used.
Figure 12 demonstrates the decreasing return in efficiency as helium-3 pressure is increased for a typical cylindrical research detector used at LANL. To emphasize the situation, a figure-of-merit (FOM) is developed that relates the efficiency, , to the partial pressure of helium-3 gas in the tube, . This FOM is referred to as cost efficiency. The m=1 case in Figure 13 represents equal priority given to the intrinsic efficiency and the quantity of gas used. The optimal partial pressure of He-3 in this regime is ΡHe-3 < 100 mbar. Figure 12 shows that the intrinsic efficiency in this scenario is at least a factor of 10 less than traditional high-pressure He-3 tubes. Thus, one geometric interpretation of this scenario assumes that total efficiency requirements can be satisfied by increasing the detector’s active area indefinitely. Values of m greater than unity represent increased emphasis on efficiency over amount of gas used. At the high end of the scale, m>2 represents the traditional viewpoint that the amount of He-3 used is of no importance at all. This scenario is not without merit; constraints on laboratory space typically limit the size of detectors so that maximizing the volumetric count rate is crucial. However, this is not feasible for large-area detectors such as those required for standoff interrogation applications because (1) the cost of packing more gas into the tubes outweighs the cost of adding additional detectors, and (2) the amount of He-3 required to deploy such a high-pressure detector system nationwide simply does not exist terrestrially. However, traditional single-tube detector designs are not efficient enough at low pressures to satisfy count rate requirements. This dilemma prompted LANL researchers to search for a new detector design that can better meet both requirements.
1.4.1 Track length and the arrayed detector concept
Monte carlo computer codes employ the concept of track length in estimating particle flux in a volume as in Eqs. (1.3) and (1.4). Using (1.5) and , the time-integrated flux is given by:
(1.11) [7] where is the total track length, or the total distance traveled by all particles of interest throughout the volume. It is important to note that includes reentrant tracks as well as secondary tracks made by particles produced in the volume. Therefore, there is an alternative to the classical method of increasing the count rate; instead of increasing in (1.3) and (1.4) by packing more gas into the tube, increase by placing an array of He-3 tubes inside a lattice of material having a high neutron albedo and good moderating characteristics. The most promising moderating materials are HDPE and/or carbon (see Figure 14).
(a) (b)
Figure 14: (a) Lattice cell containing a single He-3 tube, and (b) lattice configuration including an outer carbon reflector.
In this design, the thickness of the separating layers between the cells, or separators (C and D in Figure 14) is chosen so there is a 20-30% chance of reflection from each layer (roughly 1-2 g/cm2 for HDPE or 2-5 g/cm2 for Carbon, see Figure 15). The neutrons are thus allowed to penetrate several layers within the detector before losing a significant fraction of their initial kinetic energy. Figure 16 shows that the albedo increases after each collision due to the energy loss. Thus, the neutrons are effectively trapped within the interior of the lattice. Once trapped inside, the neutrons continue to scatter from the walls, passing through the helium-3 tubes multiple times while thermalizing gradually. The neutrons ultimately either escape or are absorbed in one of the He-3 tubes or captured by a hydrogen atom . The outer walls of the detector (with the exception of the front face) are made quite thick to minimize neutron loss by escape. The enormous increase in track length allows the experimenter to use relatively low He-3 partial pressure without sacrificing detector efficiency. The detector thus makes much more efficient use of the gas in the detector, as shown in Figure 12. The common term used to refer to such detector designs is ANDY, which is based upon an acronym for ArraYed Neutron Detector.
Figure 15: Neutron albedo for HDPE and Carbon slabs. The albedo increases monotonically with thickness and eventually saturates. The incident neutron field was a semi-isotropic Watt fission spectrum from thermal neutrons on U-235:
Figure 16: Neutron albedo versus incident neutron energy for an infinite HDPE slab.
Chapter 2 : Environmental Effects
Need intro paragraph foreshadowing contents of this chapter open source lab neutron detection efficacy
A radiation source, a target, and a detection system are the main components of an experimental apparatus which directly impact it's efficacy. An experiment which utilizes a well known and controlled source may be referred to as a closed-source experiment. A closed-response experiment describes an apparatus with a well understood and controlled detection system. A closed-response system is able to isolate the experiment from environmental factors through collimation and shielding. Characterizing an experiment as having either a closed source or response infers, using the above definition, that the unspecified component is open and as a result that the experiment is in an open-laboratory environment. A closed laboratory environment describes an apparatus in which both the radiation source and the radiation detectors are directly controlled, closed.
The open-source laboratory experiments described in this thesis predominantly use neutron sources. Neutrons with energies below 10 MeV have scattering cross-sections beyond 1 barn for many materials commonplace in the laboratory. A neutron may either elastically scatter from a nucleus or it may inelastically scatter inducing a nuclear reaction. An elastically scattered neutron will loose more energy when scattering from light nuclei as apposed to heavy, large Z, nuclei and in doing so become even more likely to scatter. A neutron with a kinetic energy of 1 MeV is 10 times more likely to elastically scatter from Hydrogen, and many other light nuclei, than a 10 MeV neutron. This property makes materials with a high hydrogen content, like water, the preferred material for moderating or reducing a neutron's energy. The large number of neutron re-scattering events which occur when neutron energies are below 10 MeV encourage the use of open source laboratory for measurements at the neutron energies.
Fast-neutron (0.1 100 MeV) counting experiments can seldom completely ignore scattering effects and are almost always conducted in an open-response laboratory. The mean free path () may be written as
where is the scattering cross-section and is the number of particles per volume. An environment composed of air at a density of 1.3 kg/m would be a mixture of several elements averaging to a molar mass of 28.97 g/mol and correspond to
- .
A 10 MeV neutron would travel \frac{m^3}{1 \times 10^{-28 m^2} 2.7 \times 10^{25} } = 1 km in air before interacting and a 1 MeV neutron would travel less than half that distance.
This is particularly true for many active interrogation applications, where the scientist may have little control over the source and its environment.
Hence, it is proposed to modify Eq. 1.3 by introducing a new term describing a given detector’s efficiency in a given environment: the efficacy:
(2.1)
where is defined to be the experimental efficiency and the two coefficients represent all environmental effects combined into two factors: the change in incident flux and the change in efficiency due to the perturbation of the neutron energy spectrum and incident geometry, respectively. Comparison of (2.1) with Eqs. (1.6), (1.7), and (1.9) reveals that the experimental efficiency is equal to the flux-weighted average total efficiency divided by an effective fractional solid angle subtended by the detector , or:
(2.2)
The efficacy, then, is the fractional increase in the number of counts in the detector, per source particle travelling directly from the source to the detector’s active surface, due to environmental interactions. In conceptual terms, the efficacy can be said to provide the connection between the closed laboratory and open laboratory. Efficacy additionally can be used to relate different open-laboratory scenarios to one another.
2.1 Understanding the two components of Efficacy
The two components are inextricably related to one another, as virtually all nuclear processes are strongly energy-dependent and involve the transfer of both energy and momentum. However, it is useful to consider them conceptually distinct, as the following sections will illustrate. As a further note, keep in mind that nearly all detectors used in nuclear science are somewhat sensitive to particles entering the detector at positions not considered part of the active area. This is particularly true for detectors that count fast neutrons by relying on external moderation to thermalize the neutrons. Therefore, it is important to remember that the detector area involved in the efficacy comprises the entirety of the detector’s outer surfaces. The surface area used for normalization, however, remains the detector’s front face, the same as used in calculating the intrinsic efficiency. 2.1.1 Effects of environmental scattering on particle flux To reiterate, is the overall change in magnitude of the particle flux entering the detector due to environmental interactions. As shown in Figure 17 below, changes in particle flux arise from many objects and processes. The challenge faced by the experimentalist is analyzing the environment and accurately determining which objects will have the greatest effect on the particle flux. A solid apriori assessment will serve as a guide for decisions such as detector placement, location and makeup of supporting apparatus, source configuration, etc. The primary considerations are the object’s solid angles relative to the source and detector and total cross-section for neutron interactions. Obviously, hydrogenous materials such as wood, oil, water, concrete, etc. near the source or detector are particularly troublesome and should generally be avoided when possible. Depending on the specific application, it is not always necessarily to measure . However, the experimenter should consider it a general requirement to at least achieve a reasonable estimate of its magnitude and take whatever steps are possible to restrict it as close to unity as possible.
Figure 17: Examples of the various scattering processes that effect the absolute particle flux incident upon the detector.
2.1.2 Effects of environmental scattering on intrinsic efficiency
For the purposes of analyzing the effect that the change in particle flux has on experimental intrinsic efficiency, it is convenient to simplify our thought processes by considering the effect that nuclear interactions have on the average energy of a large number of incident particles. Some majority nuclear interactions and their effects on both efficacy parameters are summarized below . • Attenuation: Most materials preferentially absorb thermal neutrons. Therefore, as attenuation becomes a significant effect, the neutron energy spectrum generally increases in average energy, or is hardened. Using the detector of Figure 56 on page 102 as an example, this increase in the average energy would cause an additional decrease in efficiency; thus .
Figure 18: Effects of various scattering processes on energy spectrum and particle incidence.
• In-flight scattering: Neutron scattering cross-sections globally decrease with energy for most elements, although not as universally as for attenuation. This is the case for long flight paths through atmosphere such as in standoff interrogation experiments. In this case, a significant number of neutrons can be removed by scattering but the effect on the energy spectrum is much less significant: . • Near-source scattering: This is a much more complicated situation, and can be the most difficult to accurately assess. Hydrogenous materials have a large scattering cross-section and also extract significant amounts energy from the source particles. For one example, if the source is, say, hidden in an oil drum, the flux is significantly increased because the drum has a solid angle of 4π for source particles and the detector has roughly the same solid angle for the drum and the source: . High-Z materials can have significant cross-sections but generally have a lesser effect on the particles energy: . Many middle-Z materials and a few high-Z materials have both large absorption cross-sections and large scattering cross-sections. If such materials are present, the flux and efficiency generally increases only slightly: .
Figure 19: Determination of the flux efficacy factor for neutron-scattering objects in the environment.
• Scattering from objects in the environment is generally considered to be a source-induced background effect. For environmental objects, can be calculated directly. Assuming isotropic source emission and semi-isotropic reflection from the object:
(2.3)
where I is the source current, IT is the incident current, is the source-detector solid angle, is the source-object solid angle, is the object-detector solid angle, and is the albedo of the object. Of particular concern are extensive planar surfaces such as concrete floors and walls or the surface of the ocean for maritime applications. Figure 20 shows that the albedo for concrete is 0.5-0.8 in the neutron energy regime applicable to this work. The result of such high albedo is that most of the neutrons emitted from the source have multiple opportunities to interact with the detector.
Figure 20: Neutron albedo from a thick concrete slab. The bumpiness is caused by scattering resonances in the constituents of the concrete. Notice the multiplication effect for En > 40 MeV as the cross-section for reactions producing multiple neutrons becomes significant. At even higher energies, interactions involving cascades of (n, xpxn) and (p, xpxn) reactions and (n, spallation) become possible and α eventually exceeds unity.
2.1.3 Examples of efficacy calculations and discussion
Consider, for example, a He-3 detector having surface area 200-cm2 located 1-m from an isotropic neutron source with the entire apparatus located 1m above a semi-infinite concrete floor and the source-detector axis parallel with the surface of the floor. Take , , and in (2.3). Using MCNPX, was calculated to be 6.83 x 10-3. This results in a flux-efficacy factor of . Now move the detector to a distance of 5 meters from the source. decreases by about a factor of 10, to 7.04 x 10-4 because the detector is further away from the part of the floor most strongly illuminated by the source. However, simultaneously decreases by a factor of 25, so the net result is a considerable increase in flux efficacy: .
Figure 21: Efficacy effect of nearby concrete wall on detector efficiency for an epithermal neutron spectrum simulated by MCNPX. The statistical error bars were omitted for clarity; they are less than 1%.
A suggested rule of thumb in the laboratory is to keep the efficacy ( ) below 10%. One would naturally expect the efficacy to decrease as the experimental apparatus is moved further from the wall. Figure 21 shows MCNPX calculations for the two experiments described in the preceding paragraph. Both 1-m and 5-m source-detector distances are presented for a wide range of wall distances. For a source-detector distance of 1-m, a 3-m distance from the wall is sufficient to meet the paradigm. For a 5-m distance, the experiment must be moved >15m from the wall. In summary, for a single nearby semi-infinite wall, the necessary distance to minimize the efficacy effect is roughly 3 times the source-detector distance when the source and detector are less than a few meters apart, and it is somewhat greater than that for larger separations. Note that at such distances the efficacy is almost entirely due to the increase in flux; the energy effect increases as the source-detector distance increases, but remains below ~110% in this scenario. Interestingly, the 5-m source-detector distance data actually shows a decrease in efficacy for a wall distance less than 1.5m. This effect arises due to multiple scattering in the wall. As the source-detector apparatus gets closer to the wall, the average depth of the scattering point inside the wall becomes greater and the neutrons experience an increased probability of scattering away from the detector. The effect was also observed for the source-detector spacing of 1-m. The applicable wall distance was < 0.25-m in this case, and the data was omitted in the interest of readability. Now consider the same two experiments placed inside a concrete room 10-m on a side. The neutrons are now confined on all sides and they can scatter from the walls multiple times. Using the facts that for particles emitted from the source and for wall-to-wall interactions and assuming equidistant walls and negligible fraction of neutrons absorbed in the detector on each “bounce”, Eq. (2.3) can be modified thusly:
(2.4)
Equation (2.4) grows without bound as . This is a direct result of neglecting the absorption of neutrons in the detector. Several alternative expressions for the efficacy of a box can readily be developed that do not make this assumption. Depending on other assumptions that are made, these expressions rapidly grow in complexity and become cumbersome to calculate on-the-fly. Thus, they are considered inconsistent with the spirit of the efficacy concept and are not presented here.
Comparison of the second terms of Eq. (2.3) and Eq. (2.4) shows that the impact of the box on the incident flux is much more significant than for a single wall—the efficacy is 4 times greater for ! The energy effect is also increased, as the neutrons lose more and more energy as they continue to rattle around the room. Figure 22 summarizes the effects for various locations within a 7-m-tall box:
Figure 22: The efficacy of the experimental apparatus of Figure 21 inside a 10-m square by 7-m tall concrete box simulated by MCNPX. The statistical error bars were all less than 1% and were omitted for clarity.
The data from Figure 21 and Figure 22 are given in Table 2 for easier comparison. The efficacy at the center of the box is 10 times greater than the single-wall case at a distance of 5 meters from the wall. For a detector 1-m from the source positioned 1.5m above the floor, the efficacy is increased by at least a factor of 2.5; this minimum increase logically occurs when the apparatus is in the center of the room. The magnification effect of the box increases to more than 6.5 times when the apparatus is very close to an adjacent wall. The effect is even more dramatic when the source-detector distance is increased to 5 meters—the efficacy is roughly a factor of 10 greater than the single wall no matter where you are in the room. The count rate in this situation is over eight times greater than if there were no walls present. 5-m from wall 1-m Src-Det Center of box 1-m Src-Det Distance to nearest wall in box, m In Box 1.5-m above floor 1-m Src-Det 1.5-m from wall 1-m Src-Det Distance to nearest wall in box, m In Box 1.5-m above floor 5-m Src-Det 1.5m from wall 5-m Src-Det 0.034 0.343 0.5 1.111 0.169 0.5 6.708 0.718 1.0 0.797 1.0 7.022 1.5 0.637 1.5 7.223 2.0 0.544 2.0 7.260 3.0 0.476 3.0 7.155 5.0 0.467 5.0 7.381 Table 2: Values of efficacy (κ) for concrete wall and concrete box.
2.2 The neutron gas concept
Eschewing mathematical rigor, the situation can be conceptualized in an alternate fashion by envisioning a neutron gas being emitted by the source. Albedo neutrons are analogous to pressure waves being re-emitted from nearby objects, walls, etc. that they come into contact with. These waves, being comprised of uncharged particles, do not interact with each other and can be modeled as statistical ensemble similar to an ideal gas [27]. A given experimental configuration thus creates a particular neutron gas flux-pressure gradient that the detector is subjected to in addition to the neutrons that travel directly from the source into the detector’s acceptance. The flux-pressure gradient varies with position in both magnitude and energy spectrum. If the detector were rotated about the source, the direct flux would not change but the detector would be placed in a different flux-pressure scenario. On the other hand, if the distance from the source to the detector were changed, the direct flux would change but the flux-pressure would remain unaffected. In both cases, however, the neutron gas itself remains constant.
2.3 Closing remarks on efficacy
It can be impractical to calculate wall-to-detector solid angles with any appreciable accuracy on the fly in a laboratory setting. On the practical side, it is easy to envision a small pocket reference book containing a compendium of efficacy values that can quickly be looked up for various experimental situations. Most importantly, a thorough understanding of the principles presented above can contribute invaluable insight into how much detail must be included in computer models to accurately reproduce the experiment. As a final note, the above discussion has considered the source to be completely open and uncollimated. It is frequently fairly easy to eliminate much of the efficacy effect using a neutron-absorbing collimator. Materials typically used for this purpose include polyethylene doped with boron, or b-poly, and outer sheets of Cadmium wrapped around inner layers of moderator (usually HDPE or b-poly). It is never possible to completely ignore environmental effects in high-energy neutron-counting experiments no matter how well the source is collimated, however, as significant numbers of neutrons can interact with environmental objects after scattering from the front surface of the detector or after passing through the detector entirely. However, through careful attention to details during the planning and construction phases of the experiment, environmental factors can usually either be reduced to negligible levels during the experiment or at least satisfied by simple additions to the geometry model used in the simulation.
Chapter 3 : Benchmarking Studies
The array design work was almost entirely performed with the monte-carlo radiation transport code MCNPX. A series of experiments were conducted to benchmark the abilities and limitations of MCNPX's ability to predict neutron scattering and detector response. Once benchmarked, the simulation was used to design the detector array for this thesis.
3.1 The MCNPX code
MCNPX is an extension to the MCNP code produced and maintained at Los Alamos National Laboratory. Development of MCNP and its parent codes dates back to the first nuclear reactor design work in the 1950’s. MCNP is widely regarded as the most complete and accurate coupled neutron/photon/electron transport code in the world in the energy range 0 < E < 150 MeV. MCNPX extends the capability of MCNP to include nearly all particles, including heavy ions, and much higher energies by integrating several other codes such as LAHET, CEM, etc. Active development of both codes is ongoing and new features are continually being added. The relatively new addition of light-ion production from nuclear reactions is of particular interest to this work. This gives the code the capability of producing and transporting the energetic daughter particles from several reactions, such as the proton and triton from the 3He(n,p)3H reaction. Transporting the daughter products allows for accurate representation of wall effects and also allows the user to specify a lower threshold in terms of total energy collected. This cutoff energy gives the model slightly improved accuracy in predicting count rates, as it mimics the lower-level threshold used to remove electronic noise and contributions from other particles found in experimental helium-3 spectra.
Figure 23: MCNPX pulse-height light tally of energy deposited in He-3 tube from 3He(n,p)3H reactions, broken down by particle type. The steps in the sum spectrum correspond to wall effects (see § 1.2.1.2). Notice that the peak in the proton spectrum is slightly shorter than that for the tritons; this demonstrates that more protons stop in the wall because of their greater range. There is a clear threshold at about 190 keV above which all pulses can be considered to be produced by neutron capture events.
3.2 Experimental setup Three experiments were conducted to benchmark various aspects of the ANDY detector design: 1) albedo setup, which measured the efficiency of a He-3 counter versus thickness of HDPE layer behind the detector; 2) pressure setup, which measured efficiency versus He-3 partial pressure within the detector; and 3) diffusion/reflection setup, which measured the efficiency for a quasi-lattice detector consisting of a He-3 tube sandwiched between four stacks of alternating HDPE and air layers as the thickness of the HDPE layers was increased. All three experiments used 2” diameter by 12” long drift tubes constructed and filled at LANL. The fill gas was 1 bar total pressure containing a mixture of He-3 and proportional gas.
Figure 24: Setup for efficiency vs. He-3 partial pressure experiment
Figure 25: Setup for albedo experiment
Figure 26: Setup for the diffusion/reflection (separator thickness) experiment
The experimental setups were intentionally designed in a minimalistic fashion to accentuate the desired effect and maximize repeatability. The setups generally consisted of HDPE sheets separated by cylindrical HDPE spacers to produce an air gap. The size of the HDPE sheets was 12” x 16” and the spacers were 1” diameter by 2-1/16” long. Holes 1/4" in diameter were drilled through the sheets and the center of the spacers and 1/4" HDPE rods were inserted through the entire setup to insure that all the layers were properly aligned. The detectors were placed in the air gap lengthwise with the detector axis aligned parallel to the long side of the HDPE sheets. The center of the detector was aligned with the geometric center of the sheets. The manufacturer of the HDPE sheets prescribed a range in density from 0.92-0.95 g/cm3; the density used in this set of calculations was 0.93. The statistical error in the MCNPX runs was less than 1%. The data were assigned 5% error bars to account for unquantifiable approximations in the geometry definition. The error bars assigned to the MCNPX results should not be confused with random error bars; rather, they merely suggest a magnitude for the systematic errors that are known to be present. Four different Cf-252 sources were used in the experiments. Sources no. 208, 209, and 210 were cross-calibrated using source 108 as the standard. The results are shown in Table 3. The assumed uncertainty in the activity is 10%. The source capsules were cylindrical, 0.8-cm diameter by 1-cm long. The actual active volume of the sources is not known; a 1-mm dead layer in all dimensions was used in the model.
Source Number Calibrated or Calculated Mass, μg Reference Date Experiment Date n emission rate, s-1
108 1.0 (±10%) 6/1/1987 8/9/2008 13560 ± 1360
208 0.110 (calc.) 12/31/1988 8/9/2008 1492 ± 149
209 0.214 (calc.) 12/31/1988 8/9/2008 2887 ± 289
210 0.211 (calc.) 12/31/1988 8/9/2008 2853 ± 285
Table 3: Cf-252 source data
3.3 Experimental results 3.3.1 He-3 partial pressure experiment Three detectors were tested, containing He-3 at partial pressures of 50 mbar, 150 mbar, and 300 mbar. In the MCNPX models, tubes having >1 bar total pressure contained exactly 300 mbar of proportional gas. The self-shielding effect of the He-3 gas becomes readily apparent in the model results above 300 mbar as the slope of the curve becomes less than proportionality. Having only three data points, rigorous analysis was not feasible, but on a qualitative basis the empirical data does appear to match the MCNPX calculation within 1-sigma. It would have been desirable to measure tubes containing higher He-3 pressure (>=1 bar) in order to quantify the self-shielding effect of the helium-3. This was forgone at the time due to limited quantities of helium-3 available at LANL and multiple other experiments competing for the gas. Further experiments may be performed at a future date to expand the dataset and verify the code’s predictions in the high-pressure regime.
Figure 27: Results of He-3 pressure experiment
3.3.2 Albedo experiment The purpose of the albedo experiment was to verify that MCNPX can correctly predict the increase in count rate from neutrons that backscatter from the adjacent HDPE slab. The front layer of HDPE was chosen to be 0.30 g/cm2, or 1/8” in thickness. A front moderator must be used to provide structural stability and some initial moderation of the energetic Cf-252 fission neutrons. However, the front moderator was kept as thin as possible in order to avoid interference with the albedo signal. The results of the experiment appear in Figure 28.
Figure 28: Results of Albedo experiment
There is a significant deviation at the two thinnest reflectors. This deviation is the result of low count rate compared to background. The signal-to-noise was very poor, -15dB for the thinnest reflector (1/8”, or 0.30 g/cm2). Consequently, these data points were excluded from the chi-squared analysis. The interior data points between 3/8” (0.90 g/cm2) and 6” (14.48 g/cm2) match within 1 sigma, except for a couple exceptions: there appears to be a slight deficiency (approx. 20%) in the MCNPX data at 2-3” thickness (4.83-7.23 g/cm2). This is likely due to inconsistencies in the density of the HDPE, as the slabs that were thicker than 1” were composed of multiple sheets that were cut from multiple sheets of stock. The reduced chi-squared was 0.787, showing excellent agreement considering the 10% error in source activity. It should be noted, however, that the experimental data are universally greater than the MCNPX simulation. On average, the measured count rate is 1.09 ± 1.9% times that predicted by MCNPX. This is within the uncertainty of the source activity and it can be treated as a systematic error. After applying this empirical renormalization factor, the source activity was assigned an error of 3.6%, which is the 1.9% error of the mean of the deviation combined in quadrature with a 3% error to account for the uncertainty in the source position. The new reduced chi-squared value of 1.54 is very suggestive that these assumptions were valid and the calibrated source activity is incorrect.
Figure 29: Reanalysis of albedo experiment results. In this plot, the source activity was recalibrated using an empirical correction factor of 1.09.
3.3.3 Diffusion/reflection experiment The diffusion experiment represented an attempt to reproduce the effect of the neutron “trap” created by the HDPE lattice. The simple design allows the separator layers to be easily switched out. This facilitates the study of varying separator thickness while eliminating the need to manufacture multiple lattices. The empirical data and MCNPX match very well. The small reduced chi-squared value of 0.210 is believed to be accidental. This happened because this setup produced much lower count rates than the other two experiments. To compensate for this, the source was placed directly on the front face of the detector. This resulted in much greater sensitivity to small errors in source placement than was present in the other experiments. While the source did not move appreciably between measurements, the precision of its position for simulation purposes was only known within about 5%. Thus, the empirical data and simulation just happened to almost exactly coincide; it is expected that a more precise setup would result in an over prediction of the source activity, similar to the albedo results. This conclusion was drawn at after analysis of the results presented in Chapter 6, which show strong consistency with section 3.3.2. The slope of the MCNPX curve does appear to exhibit a slightly greater increasing trend than the experimentally measured values. The reduced chi-squared analysis shows that the difference in slope is not statistically significant; however, the trend is suggestive that a systematic error may be present. The most likely error is that the assumed value of 0.93 for the HDPE density is incorrect. Ultimately, the results of the experiment are quite satisfactory. They suggest that great care should be taken for future experiments that require high sensitivity. Furthermore, greatly influential parameters such as the density of hydrogenous materials should perhaps be verified with an independent measurement.
Figure 30: Results from separator thickness experiment
3.4 Conclusion of benchmarking studies
The Monte-Carlo code MCNPX provides highly accurate predictions of helium-3 detector response for many experimental setups involving polyethylene as the primary constituent. By extension, the code can be assumed to perform very well for pure Carbon as well. The code was shown to be quite sensitive to small modifications in the setup, and it is logical to presume that it will be quite sensitive to small environmental changes as well. Therefore, much care must be taken in modeling such experiments; not only to accurately define the pieces that make up the experimental apparatus, but also to adequately identify and characterize neutron-scattering objects in the environment.
Chapter 4 : Detector array optimization
The optimization work presented here is intended to lay a general groundwork for application-specific designs of ANDY-type detectors. Therefore, a thorough investigation of a uniform rectangular HDPE lattice was performed. Different configurations may prove fruitful for enhancing efficiency; some suggestions are made at the end of this chapter. The ANDY concept provides a rich canvas for inspiring creativity and imaginative design; such tasks are left to the designers of real-world implementations. Throughout this chapter, the source used was a quasi-plane wave of Cf-252 neutrons uniformly distributed across the entire front face of the detector, including the outer sides. 4.1 Fundamental principles and parameters Limiting the scope of the study to the above paradigm allows the parameter space to be completely sampled. The analysis is further simplified by setting the thickness of the four outer walls and rear slabs to the albedo-limited thickness of 9.5 g/cm2 (see Figure 15). The only remaining parameters to optimize are the thicknesses of the front moderating slab, the sidewalls, and the separators.
Figure 31: Diagram of an ANDY-type detector, specifying the parameters to be optimized.
4.1.1 Total efficiency figure-of-merit A figure-of-merit (FOM) is defined in Eq. (4.1) to properly compare detectors of different sizes. The FOM is the intrinsic efficiency normalized to one liter He-3 at STP present in the detector. The FOM is also geometry-normalized by multiplying by the surface area of the detector. A weighting factor m is included to control the relative emphasis between efficiency and amount of He-3 used. This weighting factor represents the experimenter’s preference between greater efficiency or maximally-optimized usage of the He-3 gas.
(4.1)
where is the surface area of the detector and is the STP volume of helium-3 present in the detector. Referring to Eqs. (1.7) and (1.8) on page 15, it is readily apparent that, for m=1 this expression is proportional to the total efficiency times . It is thus referred to as the total efficiency figure-of-merit. Note that because the magnitude of FOM[m] depends on the intrinsic efficiency raised to the factor m, comparison of FOM[m]’s having different m is meaningless. To prevent this mistake, m is always denoted as a bracketed subscript. The units of FOM[1] are . It is impossible to quantify the dimensionless factor m; henceforth the units are referred to as ‘arbitrary.’ The usefulness of this figure-of-merit is that it is invariant with the number of detectors used in the experiment (assuming zero cross-talk between detectors); therefore it permits direct comparison of the effectiveness of different detector designs.
4.2 MCNPX simulations
Before proceeding with the optimization process, a baseline was obtained by performing a simple study optimizing the response of a single high-pressure tube containing 3 bars of He-3 inside a rectangular parallelepiped of high-density polyethylene.
Figure 32: Single He-3-tube detector used for baseline comparison.
4.2.1 Baseline data: single He-3 tube The tube used in the baseline simulation was 5-cm in diameter, 300-cm in length, and contained 3 bars of He-3. The total volume of He-3 in the tube was approximately 17.3 LSTP (0.77 mol). The thickness of the back reflector was chosen to be 9.5 g/cm2 and the front moderator 0.95 g/cm2. The thickness of the four outer sides was varied from 1.9 g/cm2 to 28.5 g/cm2. The results appear in Figure 33. The efficiency for the single 3-bar tube reaches a maximum of about 9.2% at 4.75 g/cm2-thick outer walls. An interesting phenomenon occurs as the wall thickness is increased beyond this point; the efficiency falls off, but the surface area simultaneously increases. The increase in surface area, and hence solid angle, initially dominates, resulting in an increase in FOM[1]. As the sidewall thickness is further increased, the two competing factors ultimately reach an impasse and FOM[1] saturates at about 33.3 above 12.35 g/cm2. This presents an interesting scenario to applications such as neutron radiation monitoring: concrete is a very effective neutron moderator and it is typically used extensively in laboratories; therefore the most efficient use of the detector is to embed the radiation monitor directly into the walls and/or floor of the facility.
Figure 33: Intrinsic efficiency and total efficiency figure-of-merit (FOM[1]) for a detector consisting of a single He-3 tube.
4.2.2 Optimizing the design of the rectangular ANDY detector The detector size was chosen to be 320-cm wide (approx.) by 320-cm tall by 20 rows deep in the direction of the incident neutron plane wave. The total depth of the detector varies as the separator thickness is changed. This is an adequate size to minimize fringe effects from the edges of the detector and thus is representative of a semi-infinite implementation. The tubes were 5-cm in diameter and 300-cm long. These dimensions are suitable to many homeland security applications while maintaining relevance to the laboratory regime. The exact width of the detector varied slightly as the sidewall thickness was changed. The number of columns in the detector was determined by choosing the odd number that made the interior width nearest to 300 cm. Using this convention there is always a column of tubes centered on the vertical bisector of the detector. The goal of these choices was to maximize consistency of the detector’s response as other detector parameters are changed. Initial parameters were chosen to be 0.95 g/cm2 separator thickness and zero sidewalls. The detector contained 59 columns of tubes in this configuration. 4.2.2.1 Front thickness optimization The front face of the detector plays two important roles: (1) it provides initial moderation of the incoming fast neutrons, which increases the detector’s efficiency, but (2) it also reflects a significant portion of the incident neutrons via albedo. The loss from albedo predominates, and the detector begins losing efficiency at a front thickness of only 1.425 g/cm2. The maximum value reached by FOM[1] is approximately 23.0; about 31% less than that for the single tube. This shortfall is not a cause for concern at this point, as the 20-row model was never assumed to be an optimal design; it merely highlights the fact that the ANDY concept cannot be extended to an indefinite number of rows. The optimal front face thickness was chosen to be 1.5 cm. This thickness results in about 2% less than peak efficiency for this particular configuration; however, the additional thermalization should prove beneficial in the final step--optimization of the number of rows.
Figure 34: Efficiency parameters vs. front face-thickness for the semi-infinite ANDY array. The surface area is constant throughout this comparison, and the two curves are identical in shape.
4.2.2.2 Sidewall thickness optimization The effect of increasing the sidewall thickness is much as one would expect: the additional thermalization provided by the sidewalls is completely overwhelmed by neutron loss to capture on hydrogen: H(n, γ)d, and the efficiency drops monotonically. Because the width of the detector is kept as near to 320 cm as possible, the number of He-3 tubes in each row is simultaneously decreasing as they are supplanted by slabs of HDPE. The decrease in He-3 volume results in a net increase in FOM[1] that produces a broad peak near 0.7125 g/cm2 sidewall thickness. The number of columns and the associated detector dimensions are summarized in Table 4.
Figure 35: Efficiency parameters vs. sidewall thickness for the semi-infinite ANDY array.
Sidewall thickness, cm (g/cm2) Columns He-3 Volume (V), L Total width, cm Surface Area (A), m2 0.00 (0.0000) 59 102.17 316.18 10.12 0.25 (0.2375) 57 98.71 320.39 10.25 0.50 (0.4750) 55 95.24 323.60 10.36 0.75 (0.7125) 51 88.32 314.27 10.06 1.00 (0.9500) 49 84.85 314.98 10.08 1.50 (1.4250) 47 81.39 326.44 10.45 2.00 (1.9000) 43 74.46 321.86 10.30
Table 4: Detector parameters vs. sidewall thickness for the semi-infinite ANDY array.
4.2.2.3 Separator thickness optimization The results of the separator thickness study show a peak at 0.475 g/cm2 separator thickness. The peak occurs at a fairly thin value because of the semi-infinite nature of the lattice; the outer HDPE box and the gas in the tubes do a fairly adequate job of trapping and thermalizing the neutrons by themselves. Increasing the amount of HDPE in the lattice creates an initial efficiency increase because of improved thermalization; however, the loss of neutron flux due to increased albedo and neutron capture on hydrogen eventually dominates, and drops. The optimum thickness chosen to use in the array depth study was 0.7125 g/cm2;--slightly greater than the thickness that produces maximum efficiency. Just as in the study of the front face thickness, the minor loss of efficiency is expected to be offset by improved thermalization for lattices containing fewer rows.
Figure 36: Efficiency parameters vs. separator thickness for the semi-infinite ANDY array. 4.2.2.4 Row-by-row study of the separator results Before proceeding to the array depth study, the results of the preceding section were analyzed on a row-by-row basis by defining the row-sum efficiency as the sum of the contributions of all the detectors in a single row:
(4.2)
Where is the intrinsic efficiency of the individual tube at position in the lattice. See Figure 31 on page 61. In Figure 37, each data point thus represents the sum of an entire row of detectors. Row 1 is at the front of the detector, and row 20 at the back. For zero separator thickness, the count rate is fairly flat with a slight bias toward the front rows of the detector. The frontward bias becomes more predominant as the separator thickness increases. Generally speaking, rows 2-3 experience the greatest count rate and the count rate decreases dramatically toward the rear of the detector. This is a clear demonstration of the lattice concept at work: for a well-moderated ANDY detector, a significant fraction of the incident neutrons are trapped and thermalized in the first few rows. The neutron flux steadily decreases through absorption and leakage through the walls of the detector as the neutrons diffuse into the deeper rows, and the count rate drops accordingly. This suggests that only a few rows of tubes may be necessary to achieve the desired efficiency. The optimal figure of merit will likely occur at even fewer rows.
Figure 37: Row-sum efficiencies of the semi-infinite ANDY detector for several separator thicknesses. Each line corresponds to a particular separator thickness. Each point on the line represents the sum of all the detectors in that particular row.
4.2.2.5 Array depth optimization Figure 38 was produced by modeling several detectors, each containing a specified number of rows of tubes. The results show that 20 rows are nearly sufficient to reach maximum possible efficiency and 90% of saturation efficiency is reached at only 10 rows. Furthermore, the efficiency for a single row is nearly equal to that of the optimized single high-pressure tube. While the efficiencies are comparable, the 1-row ANDY design enjoys a huge advantage over the single tube in terms of FOM[1]. This is because the low-pressure tubes used in ANDY arrays contain much less gas than old-style single high-pressure tubes; therefore, ANDY-type detectors occupy a much greater solid angle relative to the amount of helium-3 in the detector. In this particular arrangement, the ANDY detector has 21.5 times the surface area of the single-tube detector but only uses 5.1 times as much helium-3, resulting in an increase in FOM[1] of 2.97--nearly 3 times the total efficiency per unit gas. This result clearly demonstrates the wasteful nature of vintage He-3 detector designs.
Figure 38: Efficiency parameters versus number of detectors rows for rectangular ANDY detectors. The lattice parameters were identical in each case: 9.5 g/cm2 in the top, bottom, rear, and outer sides; 1.425 g/cm2 in front; and 0.7125 g/cm2 in the separators and sidewalls. The results from the single high-pressure tube of section 4.2.1 appear as a dashed line for comparison; the two y-axes were aligned so the efficiency and figure-of-merit for the single-tube coincide.
The figure-of-merit results are initially surprising in that the maximum FOM[1] occurs at a single row. This initially appears to be in disagreement with the results of section 4.2.2.4, which suggested that the peak should have occurred at two to three rows. As shown in Figure 39, analyzing these results on a row-by-row basis reveals the discrepancy: the row efficiency increases monotonically towards the rear of the array for detectors having only a few rows. However, FOM[1] is based on the average efficiency of all the rows, which monotonically decreases. The monotonic increase in efficiency toward the rear is partly a result the high albedo of the thick rear reflector, but is also due to insufficient thermalization that stems from the constant-thickness front moderator and separators that were used throughout this microstudy. To demonstrate this, the four-row ANDY detector was re-optimized to obtain maximum efficiency. The results are presented in Figures 40-42.
Figure 39: Row-sum efficiency analysis of ANDY arrays containing only a few rows. The average row efficiency for each detector is given by the dashed lines. Row 1 is the front row.
Figure 40: Optimizing the front moderator for the four-row ANDY lattice.
Figure 41: Optimizing the separators for the four-row ANDY lattice.
Figure 42: Row-by-row comparison of four-row ANDY detectors: poorly thermalized and optimally-thermalized.
Optimization of the four-row detector resulted in a 12% gain in efficiency. This is certainly a significant gain; however, the value of FOM[1] of 80 is still well short of the single-row ANDY detector, which appears as a dotted blue line in Figure 41. This microstudy shows that both the front moderator and the separators were too thin in the configuration used in Figure 38; this is not surprising considering that those parameters were optimized for a much deeper array. Figure 42 shows that the difference in the location of neutron capture events after optimization is dramatic—the slope of the row-by-row efficiency curve is completely inverted! Rows 1 and 2 have nearly identical efficiency in the optimized array. While these results are not intended to be all-inclusive, they do provide insights that will be quite valuable to designers of real-world ANDY arrays. However, the analysis of these results is not yet complete; recall from section 1.4 that many experimental scenarios call for increased emphasis on efficiency. Applying this concept to the ANDY array has a significant impact on the lattice dimensions, as section 4.3 will demonstrate. 4.3 Applying the results to real-world configurations The implication of the results presented in Figure 38 when applied to real-world scenarios is clear: from the purest standpoint of maximum utilization of the He-3 gas, a single row of detectors is optimal. Any required increase in count rate should be realized by adding additional detectors to the ends of the array. However, this solution may not be desirable for many applications due to space constraints or aesthetic and/or logistic considerations (consider, as an extreme example, a detector 18-cm deep and 100m long!). Thus it will frequently be preferable to increase efficiency by adding additional rows to the detector. From a design standpoint, this scenario is equivalent to stating that the intrinsic efficiency is more important than the solid angle. This can be realized mathematically by adding a second weighting parameter, n, to the figure-of-merit expression:
(4.3)
This figure-of-merit is used only to optimize the number of rows in the ANDY detector. It is thus referred to as the row-cost efficiency figure-of-merit. To reiterate, m represents the relative emphasis between efficiency and amount of He-3 gas used, and n represents the relative emphasis between efficiency and solid angle. Obviously, Eq. (4.3) is mathematically equivalent to (4.1); however, both m and n are retained to emphasize the fact that the two weighting factors should be kept separate conceptually. Notice that the subscripted brackets of Eq. (4.1) have been replaced by curly braces to distinguish the otherwise identical forms.
Combining m and n into a single parameter could result in under-emphasis of the intrinsic efficiency. For example, a weighting factor of 3 represents a fairly extreme bias, and a practical-minded designer may be tempted to reduce the factor. However, the results of this strong single bias are identical to the results given by the product of the two conservative factors m=1.5 and n=2, which represent a slight bias toward efficiency compared to the amount of gas used and a moderate bias relative to the surface area of the detector, respectively. Therefore, does yield the desired result.
Figure 43: Row-cost efficiency figure-of-merit FOM{mn} for ANDY detectors in various efficiency scenarios.
For most real-world applications, m and n are both expected to be modest; the total weighting factor will typically lie in the range 1.5-2.5. Figure 43 shows that the optimum number of rows in these circumstances for the array consisting of tubes containing 300-mbar helium-3 is 4-8. This corresponds to an intrinsic efficiency of 30-35%. The reader should keep in mind that while the 300-mbar level is considered a good starting point for demonstrative purposes, the true optimum may involve more or less partial pressure of He-3 gas. The study of this final application-dependent optimization parameter is left to the designer. Comparing the row-cost efficiency figure-of-merit results of Figure 43 to the single-tube detector shows that the single tube initially gains ground as the emphasis on efficiency is increased (see Figure 44). However, when cost is truly no object (represented by the regime ), the ANDY design is even more dominant than the purist viewpoint ( ). This remarkable result suggests that virtually any real-world neutron detector design that relies on external thermalization could be improved by implementing the ANDY concept.
Figure 44: Improvement in row-cost efficiency figure-of-merit for ANDY detector over single-tube detector for various efficiency-weighting scenarios. The number of rows in the various ANDY detectors used in each weighting scenario is the optimum number suggested by Figure 43.
Chapter 5 : Prototype development
A prototype detector was constructed at LANL for the purposes of benchmarking the results of Chapter 4 and providing a portable, high-efficiency, large-area neutron detector suitable to conducting future standoff interrogation experiments at LANL and Brookhaven National Laboratory (BNL). The final design represents a compromise between cost, portability, recommended dimensions of the lattice, and efficiency required by the experiments.
Figure 45: The ANDY prototype detector in the laboratory at LANL, containing 72 tubes arranged in a 6 row by 12 column lattice.
Figure 46: MCNPX model of the ANDY prototype. The top face in the MCNPX model is the front face. 5.1 Detector construction The helium-3 detectors were built at LANL using a design emphasizing robust and inexpensive construction. The basis for the design was one that has been used successfully for constructing proportional counters up to 6.1-m in length for the ongoing development of a muon radiography and tomography system at LANL [43, 44, 45]. The detectors consist of an aluminum tube 5.08-cm in diameter that has been sealed at both ends with welded aluminum caps. The central wire is 35-micron diameter gold-plated tungsten stretched to 50g tension. The dual anode connections (top and bottom) are provided via copper tubes 0.15875-cm in diameter that are crimped onto the central anode wire. Thus the tubes can readily be adapted to position measurements using the time difference between the signals arriving at the two ends. The anodes are insulated from the housing by polyetheretherketone (PEEK) tubing. Swagelok fittings inserted through threaded holes in the caps provide airtight seals at the Swagelok-PEEK and PEEK-anode interfaces. One end of the tube has a tee and a second Swagelok fitting. This fitting holds a second copper tube that provides the gas interface (not pictured). The ground connection is made by tightly looping copper wire around the Swagelok fitting at the small gap between the base of the fitting and the cap. The simplicity of this design allows the detectors to be easily assembled using off-the-shelf equipment at a fraction of the cost of retail industrial detectors.
Figure 47: Schematic view of detector construction.
After the tube assembly is complete, the gas-fill and quality control processes are conducted simultaneously in an integrated fashion. First, the tension in the anode wire is verified with an oscillation test. In this test, a magnet is placed near the detector to create a magnetic field gradient. The wire is caused to vibrate by gently striking the tube with a knuckle or rubber mallet. The fundamental frequency of the wire’s vibration is proportional to the square root of the tension in the wire. The wire’s motion through the magnetic field induces an oscillatory electrical signal in the wire. The frequency of oscillation is measured with a digital oscilloscope that has built-in fast fourier transform (FFT) capability (Tektronix TDS3000B or similar). Several harmonics are excited during this test. The precision of the measurement can be increased to better than 1% by fitting several of these harmonics. Next, the detectors are connected to a custom-built gas filling station that allows up to 60 tubes to be filled and leak-checked simultaneously. The first step in this process is leak checking with ordinary Helium. During the leak checking process the tubes may also be subjected to an evacuation and heating cycle, which assists in the removal of outgassing impurities. The tubes are then high-voltage tested to 5000V to insure proper isolation of the anode wire before adding the fill gases. The proportional gas is a proprietary mixture of ethane (C2H6), tetraflouromethane (CF4, industrial designation R14), and Argon. The gas is ordered premixed and arrives in a standard welding-size (approx. 50L water volume) cylinder. Helium-3 is ordered in much smaller quantities and is typically stored in cylinders about 1L in water volume. Following the leak check, the tubes are evacuated and the helium-3 is inserted. The helium-3 is added first to avoid pollution of the remaining He-3 in the cylinder. Next, the helium-3 cylinder is closed off from the rest of the system and the proportional gas is added. Using this method it is impossible to prevent some loss of helium-3 into the proportional gas cylinder. The loss is minor, however, because of the large pressure difference between the filling station and the gas cylinder. After the desired pressure is reached, the copper fill tube is closed with a crimping tool and any excess copper tubing is trimmed off. The tip of the tube is then given a secondary seal with a layer of solder. A final leak check is performed by immersing the tips of the copper fill tube and anode tubes in water. If no bubbles form, the tube is ready to go into service. 5.2 Array construction The prototype consists of 72 helium-3 tubes arranged in a 12 x 6 rectangular lattice. Based on the results of Chapter 4, the design of this lattice emphasizes efficiency fairly strongly. Portability was also a significant factor in choosing the dimensions; the detector is typically placed on a wheeled cart and the 12 x 6 lattice provides enhanced stability as it is rolled about the laboratory. Each tube is 5.08-cm in diameter, roughly 121.92-cm long, and contains 200 mbar He-3 and 800 mbar proportional gas for a total internal pressure of 1 bar. The dimensions of the outer box were selected to minimize weight while not unnecessarily sacrificing efficiency. The top, bottom, front and side HDPE slabs are 2.54-cm thick and the rear is 5.08-cm. The top and bottom slabs are drilled through to allow the anode connections and fill tube to pass through. There is a 3.81-cm air space and additional 2.54-cm base below the bottom slab. The open space is reserved for custom electronics that will be installed at a future date . The top area is open save for six aluminum project boxes that provide connection points for high voltage and ground wires. The entire detector is encased in a 0.762-mm thick aluminum faraday shield to reduce electronic noise.
Figure 48: ANDY Prototype assembly
The lattice is comprised of nested structures of HDPE sheets that interleave in a similar fashion to old-style egg crates. Each sheet is cut through to its midpoint lengthwise to allow the sheets to slide together and form a structure without gaps. There are six inner “egg crates” that hold 12 tubes each, made from 0.635-cm and 1.27-cm thick sheets arranged in a 3x2 pattern, respectively. The larger outer egg crate is made from 1.27-cm thick sheets arranged in a 2x1 pattern to hold the six inner lattices. This design greatly speeds assembly of the detector; each egg crate can be assembled by a single person and stands upright by itself. This allows them to be assembled independently while the outer box is being bolted together. The large egg crate is placed inside the detector before the four outer walls are closed. The small inner egg crates, on the other hand, are light enough to be lifted above the outer walls and gently dropped inside by a single person. A team of three workers can assemble the entire HDPE lattice structure in a matter of minutes. The fully-assembled weight of the detector, including helium-3 tubes, is about 650 pounds.
5.3 Electronics and readout
Data collection for the ANDY prototype is greatly simplified by combining groups of tubes in parallel. This is done by simply daisy-chaining the high-voltage and ground connections. The number of tubes that are combined and their positions in the array depend on the data that is desired. Typically, all 72 tubes are connected into one signal to facilitate gross count rate monitoring with a single data acquisition (DAQ) channel. Other experiments dictate different detector combinations; for example, 12 tubes comprising one entire row were connected to obtain the row-by-row benchmarking data of sections 6.1 and 6.2.
Figure 49: Electronics used in recording neutron counts from ANDY prototype detector. Groups of He-3 tubes are connected in parallel and recorded as a single channel using standard NIM electronics.
The benefits to this technique are clear: standard NIM instrumentation can be used; only one set of electronics needs to be set up; and standard histogramming software can be used to record the data, which results in simple and straightforward output files. There is no need to set up and calibrate complicated multichannel instruments or program elaborate data acquisition routines. There are drawbacks to this method, however: • The proportional counters must be gain-matched, as there is no independent gain control for individual tubes. Each tube is independently efficiency-calibrated prior to installation in the array and any outliers are discarded. After a matched set of tubes has been selected and installed, the neutron counts form a single, slightly rounded peak in the energy spectrum (see Figure 50). This peak plays the same important role as with a single tube; it allows the experimenter to identify neutron events and discriminate them with a lower-level threshold. The system is insensitive to gain changes on the order of a few percent because of the roundness in the peak. A gain drift is considered problematic when an additional peak appears in the spectrum. At this point, a single lower-level threshold may not be sufficient to discriminate neutron events. In the event of such a failure, each tube would have to be re-tested on an individual basis. Testing is a quick process that does not require the tubes to be removed from the lattice. Any anomalous tube(s) can also be replaced without disturbing the other tubes in the array. • A more robust DAQ system would count each detector individually. The system currently used is count-rate-limited compared to such a system, in that pileup occurs if multiple tubes detect neutrons simultaneously. Many of these pileup events could be recovered by implementing additional lower-level threshold(s) above the primary neutron peak and multiplying counts in this region by the appropriate factor (2, 3, etc). However, this correction becomes increasingly inaccurate as the pileup increases and it is preferable to limit the count rate so only single-count events occur.
Figure 50: The pulse-height spectrum from the ANDY prototype with all 72 tubes in parallel compared to a single He-3 detector. The spectrum is considerably noisier than the single-tube spectrum but the neutron peak is still clearly resolved.
• Another count rate limitation occurs in the form of increased saturation recovery time. When a proportional detector receives an overwhelmingly large burst of radiation, the voltage in the tube is depleted and the tube is said to be in saturation. The bias voltage is typically quickly replenished in a matter of microseconds to milliseconds by capacitive storage. During the initial recovery phase the detector is operating proportionally, but at reduced gain. Recovery time is exacerbated in this system because of the large number of detectors that need to be “recharged” and the varying degree of depletion. The tubes at the front of the detector experience greater depletion and longer recovery time than the tubes at the rear because the rear tubes are partially shielded by the additional HDPE layers in front of them. The causes the neutron peak to appear “smeared out” because the tubes are not all operating at the same gain. The data cannot be considered valid until all tubes have recovered and a single, cohesive neutron peak appears. During recent proton interrogation experiments conducted at LANL the recovery time for the ANDY prototype was several seconds at a 30-m distance, while that for a single 2”x12” He-3 detector at a distance of 1m recovered in a few milliseconds. • Experiments involving multiple groups of detectors (such as sections 6.1 and 6.2) require repeated measurements. Repeatedly switching detector connections to perform multi-group measurements takes time and is potentially hazardous to the experimenter and the detectors themselves. The anode connections on the detectors are somewhat fragile and due to the finite capacitance of the tubes the experimenter must take care that they are completely drained of charge or (s)he may receive a small but unpleasant shock. The anode connections are also fairly sharp and superficial scratches can occur if they are carelessly brushed up against. While the potential for accident is low when proper precautions are taken, it would still be preferable to eliminate the risk altogether by implementing a multichannel counting system that does not require the detector lid to be removed. The drawbacks discussed above make it desirable to develop the capability to record each detector individually for long-term use of the detector. However, the daisy-chain method is perfectly satisfactory for occasional use around the laboratory, particularly when the count rates are modest. It is much more convenient for the experimenter to quickly set up a simple single-channel acquisition system than to deal with a complex 72-channel data acquisition system and struggle to re-learn the nuances that are always present in such systems. Therefore, despite the limitations of the existing method, development of such a system has been given a low priority up to this point .
Chapter 6 : Experimental results
Two benchmarking experiments were conducted to verify the ability of the MCNPX code to predict the performance of the ANDY prototype detector at LANL. 6.1 Individual tube efficiency measurement In the first experiment, the efficiency was measured at each of the 72 detector positions using a Cf-252 neutron source inside an HDPE source holder attached to the front of the detector. Several precautions were taken in order to maximize the consistency throughout the experiment: First, the source holder was keyed so it could only be attached in one position, insuring precise repeatability in the source position between background and foreground measurements. Second, all of the available He-3 tubes were counted individually and twelve were selected that had the closest-matching efficiency. These twelve tubes were then inserted into row six—the back row of the lattice. The tube in column A was counted both with and without the source. Then the tubes in columns A and B were switched and column B was counted. Then B and C were switched, and so on. Hence, the same helium-3 tube was counted in every position. The twelve tubes were then moved into row five and the process was repeated. This procedure was repeated for the remaining four rows, again continuing to use the same tube for each measurement. As a final precaution, another helium-3 tube was placed 10m from the apparatus to provide an independent measurement of the background rate. This was important because the signal-to-noise ratio for the tubes having the lowest count rates was less than 2:1. The background rate did not vary significantly throughout the experiment.
Figure 51: Results of individual-tube efficiency measurement. The results are presented in rows, with each successive row separated by a decade for clarity.
Figure 51 shows the excellent agreement between the experimental data and the MCNPX model. The reduced chi-squared value of 0.388 shows good agreement but suggests that the assumed 10% error in the source activity may be excessive. Overall, the experimental values are higher than the MCNPX predictions by 6.1%. This result is consistent with section 3.3.2, where the empirical data was 9.0% greater than the code. Furthermore, the experimental curves also appear to be slightly flatter across each row, which is consistent with the results of section 3.3.3. While these deviations are not statistically significant, such consistency suggests that something is not entirely correct in the model. Several factors could create a minor effect such as this. Possibilities include incorrect HDPE density; incorrect treatment of thermal neutrons; air temperature, density, and/or humidity; or approximations in the geometry, to name just a few. The important thing, however, is that these results prove that the code is able to predict efficiencies of helium-3 detectors within a few percent. This level of precision is certainly suitable to facilitate high-fidelity planning of very sensitive experiments.
6.2 Single-row efficiency measurement with full array The purpose of the second experiment was twofold: (1) verify the MCNPX-predicted efficiency of the ANDY prototype, and (2) benchmark the code in a more difficult experimental environment. To achieve the latter, the prototype was placed in the high-resolution-spectrometer (HRS) dome at LANSCE Area C at LANL. The HRS dome is a 14-m radius circular concrete room capped with a 0.46-m thick hemispherical concrete dome . The dome is covered by a compacted-earth berm that is 3-m thick at its thinnest point. This construction provides an ideal neutron scattering trap. The detector was placed on a wooden cart 13.3 cm high and located about 5 meters from the nearest concrete wall.
Figure 52: Cross-sectional view of the HRS Dome at LANSCE Area C.
Figure 53: Results of row-sum efficiency measurement with full ANDY array including only the concrete floor in the MCNPX model. The MCNPX data was assigned 5% error bars to account for approximations in the detector and source models.
Figure 53 was created by summing each row of tubes individually. Only the source, detector, and concrete floor were included in the MCNPX model. The reduced chi-square value of 2.07 shows marginal agreement. Overall, the MCNPX results are 11.6% less than the experimental data. The intrinsic efficiency calculated by MCNPX was 20.2%, 13.0% less than the measured value of 23.2%. These deficiencies are comparable to but slightly greater than those from the results presented in Chapter 3. Conversely, the differences are also within the expected range of the efficacy from Chapter 2. Consequently, an improved model is required to determine if these results are consistent with the results of Chapter 3. The question, then, is what details need to be added to the model to obtain a sufficiently precise result? In this case the choice was fairly straightforward; the experiment and code are already very close to agreement, so the simulation was repeated, this time including the circular walls and dome in the model.
Figure 54: Results of row-sum efficiency measurement with improved MCNPX model.
Adding the concrete dome to the model had a small but profound impact on the results. The reduced chi-square value of 0.896 suggests much better agreement than the first model. The average deficiency in the row sums decreased to 7.6% and the difference in intrinsic efficiency was reduced to 7.2%.Both figures are now well within 1-sigma agreement with the earlier results. Now it can certainly be stated with confidence that the calibrated source activity is too low by 6-9%, as was originally suggested in Chapter 3.
Chapter 7 : Conclusion
Computer simulations with the MCNPX code predict an increase in cost efficiency of 2.5-3.5 for neutron detectors based on an array of low-pressure helium-3 drift tubes (ANDY-type detector) over conventional high-pressure tubes. A prototype ANDY detector was designed and constructed at LANL. The results were validated by conducting several benchmarking experiments. All of the experiments showed agreement at the 1-sigma level between the MCNPX computer model and measured data. The results were consistent enough to suggest a correction factor of 6-9% for the activity of several Cf-252 sources that are frequently used at LANL. The concept of efficacy was introduced as a deterministic method of calculating changes in detector count rate that arise from neutrons scattering from objects in the environment. A successful series of neutronics benchmarking experiments reinforces this concept. The results presented herein provide the groundwork for the design of large-area neutron detectors that will be used in Homeland Security applications. More importantly, this work paves the road toward successful management of limited worldwide helium-3 resources for many years to come.
7.1 Additional Work Several additional studies are underway to extend this work. A few of these are briefly presented below: 7.1.1 Addition of boron lining for further increase in efficiency The efficiency of low-pressure gaseous neutron detectors can be increased by adding a boron lining. Work is currently underway at LANL to develop this technology in a robust and cost-effective manner. Figure 55 shows an early initial result. The efficiency of this particular helium-3 detector was increased by nearly 20%. Details of the methods being investigated are proprietary.
Figure 55: Pulse-height spectrum of a 3He-10B hybrid detector. Key features identifying the daughter particles from both isotopes are clearly distinguishable.
7.1.2 Energy selection via external shielding The response curve of ANDY-type detectors as a function of neutron energy can be tailored to a desired neutron flux spectrum by adding external neutron moderators and/or absorbers. Figure 56 shows a few examples:
Figure 56: Efficiency curves for the ANDY prototype with several external shielding scenarios simulated with MCNPX.
7.1.3 External Monitoring for Dosimetry and Experimental Support
The high sensitivity of the ANDY prototype detector also makes it very useful for external monitoring applications. These can include dose measurements taken outside primary shielding walls as demonstrated in Figures 57-59 or as a sanity check to verify that beam was delivered, to name just a few.
Figure 57: The ANDY Prototype in operation outside the primary shielding door at Area C at LANSCE (HRS dome).
Figure 58: Overhead view of the HRS dome. The blue line is the path of the proton beam.
Figure 59: Time response of ANDY prototype during proton beam tuning.