Phi Dependent Components
Jump to navigation
Jump to search
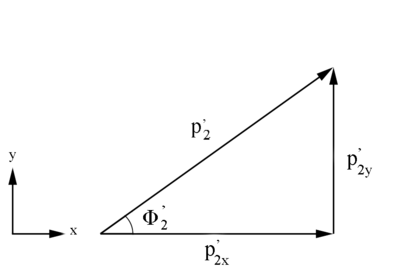
Figure 4: Definition of Moller electron variables in the Lab Frame in the x-y plane.
Similarly,
where
and using
this gives
which gives
Similarly, using
Since only the z direction is considered to be the relativistic direction of motion, this implies that the x and y components are not effected by a Lorentz transformation and remain the same in the CM and Lab frame. Holding the angle Phi constant at an initial value of 10 degrees, allows us to find the x and y components.

Checking on the sign from the cosine results for
We have the limiting range that must fall within:

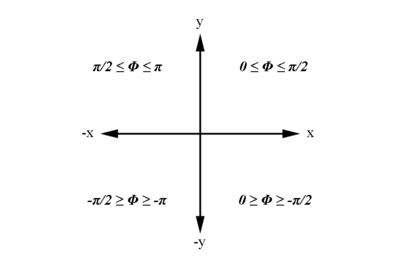
Examining the signs of the components which make up the angle in the 4 quadrants which make up the xy plane: