The Nuclear Force
Deriving the Coulomb Force
TF_DerivationOfCoulombForce
- Poisson's Equation
- [math]\nabla^2 \phi(\vec{\eta}) = - \frac{e}{\epsilon_0} \delta(\vec{\eta})[/math]
The Deuteron
Nucleon- Nucleon scattering
Cross section
- Total cross section
- [math]\sigma[/math] = [math]\equiv \frac{\# particles\; scattered} {\frac{ \# incident \; particles}{Area}} = \frac{j_{scattered} A}{j_{incident}}[/math]
- [math]j =[/math] current density = # scattered particles per Area.
Particles are scattered in all directions. Typically you measure the number of scattered particle with a detector of fixed surface area that is located a fixed distance away from the scattering point thereby subtending a solid angle as shown below.
- Solid Angle
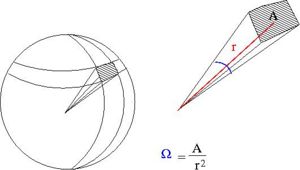
- [math]\Omega[/math]= surface area of a sphere covered by the detector
- ie;the detectors area projected onto the surface of a sphere
- A= surface area of detector
- r=distance from interaction point to detector
- [math]\Omega = \frac{A}{r^2} [/math]sterradians
- [math]A_{sphere} = 4 \pi r^2[/math] if your detector was a hollow ball
- [math]\Omega_{max} = \frac{4 \pi r^2}{r^2} = 4\pi[/math]sterradians
- Differential cross section
- [math]\sigma(\theta)[/math] = [math] \frac{d \sigma}{d \Omega} \equiv \frac{\frac{\# particles\; scattered}{solid \; angle}} {\frac{ \# incident \; particles}{Area}}[/math]
- Units
- Cross-sections have the units of Area
- 1 barn = [math]10^{-28} m^2[/math]
- [units of [math]\sigma(\theta)[/math]] =[math]\frac{\frac{[particles]}{[sterradian]}} {\frac{ [ particles]}{[m^2]}} = m^2[/math]
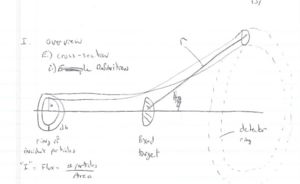
- Fixed target scattering
- [math]N_{in}[/math]= # of particles in = [math]I \cdot A_{in}[/math]
- [math]A_{in}[/math] is the area of the ring of incident particles
- [math]dN_{in} = I \cdot dA = I (2\pi b) db[/math]= # particles in a ring of radius [math]b[/math] and thickness [math]db[/math]
Scattering Length (a)
- Definition
- [math]a^2 = \frac{1}{4 \pi} \lim_{k \rightarrow 0} \sigma[/math]
While scattering length has the dimension of length it really represents the strength of the scattering (probability of scattering). It effectively give the amplitude of the scattered wave.
- Note
- the above definition is essentially an expression of how the low energy cross section corresponds to the classical value of [math]4 \pi a^2[/math]
- [math]\sigma[/math] = scattering cross-section [math]\equiv \frac{\# particles\; scattered} {\frac{ \# incident \; particles}{Area}}[/math]
- classically: the number of particles scattered = number of incident particles (the collision probability is unity)
- Area = [math] \pi a^2[/math] = The area profile in which a collision occurs
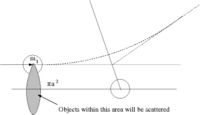
[math]\sigma = \frac{{N}}{\frac{ N}{\pi a^2}} = \pi a^2[/math]
To derive an expression for the scattering length lets start with a general expression for a scattered wave.
- A general scattered wave function has the form
- [math]\Psi_g = \frac{1}{(2 \pi)^{3/2}} \left [ e^{i \vec{k} \cdot \vec{r}} + f(q) \frac{e^{ikr}}{r}\right ][/math]
The first term represents a plane wave and the second term represent a modification of the plane wave due to the scattering in terms of the scattering probability [math]|f(q)|^2[/math].
From our previous phase shift calculation, Schrodinger solutions tend to have the general form
- [math]\Psi_S = \sum_{\ell} A_{\ell} P_{\ell} [\cos(\theta)] \frac{U_{\ell}(r)}{kr}[/math]
- [math]= \sum_{\ell} A_{\ell} P_{\ell} [\cos(\theta)] \frac{\sin(kr - \frac{\ell \pi}{2} + \delta_{\ell})}{kr}[/math] (our previous solution was for [math]\ell=0[/math])
where
the angular part is given as
- [math] P_{\ell} \cos(\theta)[/math]
and the radial part is
- [math]\frac{U_{\ell}(r)}{r}[/math]
By comparing our general solution from the phase shift and our schrodinger solution we can cast f(q) in terms of the phase shift [math]\delta_{\ell}[/math] and then define the cross section as
- [math]\sigma = \int |f(q)|^2 d \Omega[/math]
in order to get a gereral expression for a scattering cross section which we then take the limit of the momentum going to zero in order to get a general expression for the scattering length.
- Math trick to recast plane waves
- [math]e^{i\vec{k} \cdot \vec{r}} = 4 \pi \sum_{\ell m} i^{\ell} Y^*_{\ell m}(\hat{k}) Y_{\ell m}(\hat{r}) J_{\ell m}(|k| |r|)[/math]
where
- [math]\hat{k}[/math] and [math]\hat{r}[/math] are the [math]\theta[/math] and [math]\phi[/math] directions of [math]\vec{k}[/math] and [math]\vec{r}[/math] respectively.
To determine the scattering length we will be looking at [math]k \rightarrow 0[/math] so let [math]\hat{k}=0 \Rightarrow \theta=0 , \phi=0[/math] use the approximation
- [math]Y^*_{\ell m}(\theta=0,\phi=0) = \sqrt{\frac{2 \ell +1}{4 \pi}}\delta_{m,0}[/math]
- using the above to recast [math]\Psi_g[/math] to look more like [math]\Psi_S[/math]
- [math]\Psi_g = \frac{1}{(2 \pi)^{3/2}} \left \{ 4 \pi \sum_{\ell} i^{\ell} \sqrt{\frac{2 \ell +1}{4 \pi}}\delta_{m,0} Y_{\ell m}(\hat{r}) J_{\ell m}(|k| |r|) + f(q) \frac{e^{ikr}}{r} \right \}[/math]
- [math]\delta_{m,0} Y_{\ell m}(\hat{r}) =Y_{\ell 0}(\hat{r}) = \sqrt{\frac{2 \ell +1}{4 \pi}} P_{\ell} [\cos(\theta)][/math]
- [math]\Rightarrow \Psi_g = \frac{1}{(2 \pi)^{3/2}} \left \{ \sum_{\ell} i^{\ell} (2 \ell +1) P_{\ell} [\cos(\theta)] J_{\ell m}(|k| |r|) + f(q) \frac{e^{ikr}}{r} \right \}[/math]
- which we want to compare to \Psi_S
- [math]\Psi_S = \sum_{\ell} A_{\ell} P_{\ell} [\cos(\theta)] \frac{\sin(kr - \frac{\ell \pi}{2} + \delta_{\ell})}{r}[/math]
Using the identities:
- [math]\sin(kr - \frac{\ell \pi}{2} + \delta_{\ell}) = \frac{e^{i(kr - \frac{\ell \pi}{2} + \delta_{\ell})} - e^{-i(kr - \frac{\ell \pi}{2} + \delta_{\ell})}}{2i}[/math]
- [math]J_{\ell m}(|k| |r|) = \frac{e^{i(kr - \frac{\ell \pi}{2} )} - e^{-i(kr - \frac{\ell \pi}{2} )}}{2ir}[/math]
- By equating the two solutions
- [math]\Psi_S = \Psi_g[/math]
- [math]e^{-ikr} \Rightarrow A_{\ell} e^{i\delta_{\ell}} = \frac{i^{\ell} (2 \ell +1)}{(2 \pi)^{3/2}}[/math]
[math]e^{+ikr} \Rightarrow [/math]
- [math]\sum_{\ell} \frac{A_{\ell}}{kr} P_{\ell} [\cos(\theta)]e^{i (kr - \frac{\ell \pi}{2} + \delta_{\ell})} = \sum_{\ell} \frac{i^{\ell} (2 \ell +1)}{(2 \pi)^{3/2} 2ikr} P_{\ell} [\cos(\theta)]e^{i(kr - \frac{\ell \pi}{2} )} + \frac{f(q) e^{ikr}}{(2 \pi)^{3/2}r}[/math]
- [math]\Rightarrow \frac{f(q) e^{ikr}}{(2 \pi)^{3/2}r}= \sum_{\ell} \frac{ P_{\ell} [\cos(\theta)]}{2ikr} e^{- i \ell \pi/2} \left ( \frac{A_{\ell}}{kr} e^{i (kr - \frac{\ell \pi}{2} + \delta_{\ell})} - \frac{i^{\ell} (2 \ell +1)}{(2 \pi)^{3/2}} e^{i(kr - \frac{\ell \pi}{2} )} \right ) [/math]
- [math]= \sum_{\ell} \frac{A_{\ell}}{kr} e^{i (kr - \frac{\ell \pi}{2} + \delta_{\ell})} - \frac{i^{\ell} (2 \ell +1)}{(2 \pi)^{3/2} 2ikr} P_{\ell} [\cos(\theta)]e^{i(kr - \frac{\ell \pi}{2} )}[/math]
- [math]\Rightarrow f(q) = \frac{1}{k} \sum_{\ell} (2 \ell + 1 ) P_{\ell} [\cos(\theta)] \sin(\delta_{\ell}) e^{i \delta_{\ell}}[/math]
- [math]\sigma = \int | f(q) |^2 d \Omega[/math]
- [math]= \sum_{\ell \ell^{\prime}} \int \frac{2 \ell + 1 )(2 \ell^{\prime} + 1)}{k^2}P_{\ell} [\cos(\theta)] \sin(\delta_{\ell}) e^{i \delta_{\ell}} P_{\ell^{\prime}} [\cos(\theta)] \sin(\delta_{\ell^{\prime}}) e^{-i \delta_{\ell^{\prime}}}[/math]
- [math] \int P_{\ell} P_{\ell^{\prime}} d \theta = \frac{2}{2 \ell + 1} \delta_{\ell \ell^{\prime}}[/math]
- [math]\Rightarrow \sigma = \frac{4 \pi}{k^2} \sum_{\ell} (2 \ell +1 ) \sin^2(\delta_{\ell})[/math]
- [math]a^2 = \frac{1}{4 \pi} \lim_{k \rightarrow 0} \sigma = \frac{1}{4 \pi} \lim_{k \rightarrow 0} \frac{4 \pi}{k^2} \sum_{\ell} (2 \ell +1 ) \sin^2(\delta_{\ell})[/math]
For S-wave scattering [math]\ell =0[/math]
- [math]\Rightarrow a = \pm \lim_{k \rightarrow 0} \frac{\sin(\delta_0)}{k}[/math]
To keep "a" finite the phase shift [math]\delta_{\ell}[/math] must approach zero at low energy
- [math]\Rightarrow a = \pm \lim_{k \rightarrow 0} \frac{\delta_0}{k}[/math]
Singlet and Triplet States
Our previous calculation of the total cross section for nucleon nucleon scattering using a phase shift analysis gave
- [math]\sigma = \frac{4 \pi}{k_2^2}\sin^2(\delta_0)[/math]
assuming [math]\ell[/math] =0.
When solving Schrodinger's equation for a neutron scattering from a proton we were left with the transcendental equation from boundary conditions
- [math]\alpha \equiv k_1 cot(k_1R) = k_2 cot(k_2R + \delta)[/math]
- [math]\sigma = \frac{4 \pi}{ k_2^2 + \alpha^2} \left [\cos(k_2 R) + \frac{\alpha}{k_2} \sin(k_2R)\right ][/math]
In the case of a Deuteron bound state
- [math]\ell =0[/math] and [math]S=1[/math]
- R = 2 fm
- [math]\alpha[/math] = 0.2 /fm
when [math]k_2 \rightarrow 0[/math]
- [math]\frac{\sin(k_2 R)}{k_2} = R[/math]
- [math]\cos(k_2 R) = 1[/math]
then
- [math]\lim_{k_2 \rightarrow 0} \sigma = \frac{4 \pi}{ 0 + (0.2)^2} \left [1 + (0.2) 2\right ] \left ( \frac{1 barn}{100 fm^2}\right)= 4.4 barns[/math]
Experimentally the cross section is quite a bit larger
- [math]\sigma_{Exp}[/math] = 20.3 b
Apparently our assumption that the dominant part of the cross section is S=1 is wrong. There also exists a spin singlet (S=0) contribution to the cross section.
When the neutron and proton interact (create a bound state or an intermediate state) their spins can couple to either a net value of S=0 or S=1. There is only one component along the quantization axis in the event that they couple to an S=0 state. There are 3 possible components ([math]S_z[/math] = -1/2, 0 . + 1/2) in the event that they couple to an S=1 state.
If you sum up the two possible cross-section,[math] \sigma_S[/math] and [math]\sigma_T[/math], then you must weight them according to the possible psin compinations such that
- [math]\sigma_{tot} = \frac{3}{4} \sigma_T + \frac{1}{4} \sigma_S[/math]
- Solving for [math]\sigma_S \Rightarrow[/math]
- [math]\sigma_S = 68[/math] barns
Because the cross sections depend on the spin date we can conclude that
- The Nuclear Force is SPIN DEPENDENT
- Also
- Using the spatial wave functions for the singlet and triplet state one can deduce that
- [math]a_T[/math] = + 6.1 fm [math]\Rightarrow[/math] there is a triplet np bound state
- [math]a_S[/math] = - 23.2 fm [math]\Rightarrow[/math] there is NO singlet np bound state
Doing similar but more complicated calculations for p-p and n-n scattering results in
- [math]a_{p-p}[/math] = -7.82 fm [math]\Rightarrow[/math] there is NO pp bound state
- [math]a_{n-n}[/math] = -16.6 fm [math]\Rightarrow[/math] there is NO nn bound state
The Nuclear Potential
From the above we have found information on the range of the nuclear force, it's spin dependence, and it's ability to create non-spherically disrtibuted systems (quadrupole moments).
The Central Potential
No matter what potential Well geometry we choose for the nucleon, we consistently find a term which is purely radial in nature (a Central term).
- [math]\lt V_c(r)\gt = \int U^*(r) V_c(r) U(r) dr = \frac{\hbar (\ell + 1) \ell}{2m} \int |U(r)|^2G(\delta) \frac{dr}{r^2} [/math]
where
- [math]G(\delta)[/math] = a parameterization of[math] V_c[/math] which is constrained by scattering phase shift information.
The Spin Potential
We know from the lack of a p-p [math](^2NHe)[/math] or n-n bound system that the nuclear force is strongly spin dependent. This is reenforced even more based on our observations of the S=1 n-p bound state (the Deuteron).
Experiments also indicate that parity is conserved to the [math]10^{-7}[/math] level. [math]\Rightarrow[/math] experiments with an relative precision of [math]\frac{\Delta X}{X} \gt 10^{-7}[/math] have yet to find a parity violation.
- [math]\Rightarrow[/math] The spin potential would have terms involving spin scalar quantities because a spin potential with terms that are linear combinations of spin would violate parity.
Consider a spin potential function such that the total spin is given by
- [math]\vec{S} = \vec{s}_1 + \vec{2}_2[/math]
The scalar spin quantity [math]S^2[/math] would be given by
- [math]\vec{S} \cdot \vec{S} = s_1^2 + 2\vec{s}_1 \cdot \vec{s}_2 + s_2^2[/math]
or
- [math]\vec{s}_1 \cdot \vec{s}_2 = S^2 -s_1^2-s_2^2[/math]
Spin Singlet
if
- S=0
then
- [math]\lt \vec{s}_1 \cdot \vec{s}_2 \gt = \lt S^2\gt -\lt s_1^2\gt -\lt s_2^2\gt [/math]
- [math]= \left [ S(S+1) - s_1(s_1+1) - s_2(s_2+1) \right ] \frac{\hbar^2}{2}[/math]
- [math]= \left [ 0(0+1) - \frac{1}{2} (\frac{1}{2}+1)- \frac{1}{2} (\frac{1}{2}+1)\right ] \frac{\hbar^2}{2}[/math]
- [math]= - \frac{3}{4} \hbar^2[/math]
Spin Triplet
if
- S=1
then
- [math]\lt \vec{s}_1 \cdot \vec{s}_2 \gt = \lt S^2\gt -\lt s_1^2\gt -\lt s_2^2\gt [/math]
- [math]= \left [ S(S+1) - s_1(s_1+1) - s_2(s_2+1) \right ] \frac{\hbar^2}{2}[/math]
- [math]= \left [ 1(1+1) - \frac{1}{2} (\frac{1}{2}+1)- \frac{1}{2} (\frac{1}{2}+1)\right ] \frac{\hbar^2}{2}[/math]
- [math]= + \frac{1}{4} \hbar^2[/math]
Construct the Spin Potential
Let
- V_1(r) = spin singlet parameterized potential
- V_3(r) = spin triplet parameterized potential
Then
- V_s(r) = - (
Yukawa Potential
Forest_NucPhys_I


