Difference between revisions of "Neutron Polarimeter"
| (100 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | [ | + | [https://wiki.iac.isu.edu/index.php/Roman_calculation Go Back] |
= Four-vector Algebra = | = Four-vector Algebra = | ||
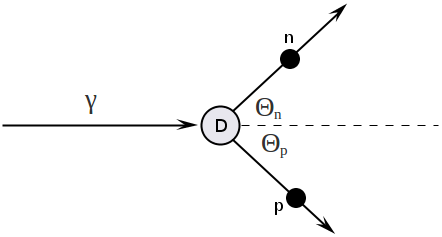
| − | + | Consider two body reaction <math>D(\gamma, n)p</math>: | |
| + | [[File:Collision01.png | 450 px]] | ||
| − | + | ||
| + | Write down four-momentum vectors before and after reaction: | ||
<math> p_{\gamma} = \left( T_{\gamma},\ T_{\gamma},\ 0,\ 0 \right) </math> | <math> p_{\gamma} = \left( T_{\gamma},\ T_{\gamma},\ 0,\ 0 \right) </math> | ||
| Line 14: | Line 16: | ||
<math> p_{p} = \left( E_p,\ \ p_p\cos \Theta_p,\ \ p_p\sin \Theta_p,\ \ 0 \right) </math> | <math> p_{p} = \left( E_p,\ \ p_p\cos \Theta_p,\ \ p_p\sin \Theta_p,\ \ 0 \right) </math> | ||
| − | + | Now apply the law of conservation of four-momentum vectors: | |
<math> p^{\mu}_{\gamma} + p^{\mu}_D = p^{\mu}_p + p^{\mu}_n\ \ \Rightarrow \ \ p^{\mu}_p = p^{\mu}_{\gamma} + p^{\mu}_D - p^{\mu}_n</math> | <math> p^{\mu}_{\gamma} + p^{\mu}_D = p^{\mu}_p + p^{\mu}_n\ \ \Rightarrow \ \ p^{\mu}_p = p^{\mu}_{\gamma} + p^{\mu}_D - p^{\mu}_n</math> | ||
| Line 22: | Line 24: | ||
<math> m_p^2 = m_D^2 + m_n^2 + 2T_{\gamma}\cdot m_D - 2m_D\cdot E_n - 2\left( T_{\gamma}E_n - T_{\gamma}p_n\cos\Theta_n\right) </math> | <math> m_p^2 = m_D^2 + m_n^2 + 2T_{\gamma}\cdot m_D - 2m_D\cdot E_n - 2\left( T_{\gamma}E_n - T_{\gamma}p_n\cos\Theta_n\right) </math> | ||
| + | = Detector located at <math>\Theta = 90^o</math> case= | ||
| − | |||
| + | Detector is located at <math>\Theta_n = 90^o</math>, and the formula above is simplified: | ||
| − | + | <math> m_p^2 = m_D^2 + m_n^2 + 2\ T_{\gamma}\cdot m_D - 2\ m_D\cdot E_n - 2\ T_{\gamma}E_n </math> | |
| − | |||
We can easily solve the equation above with respect to incident photon energy: | We can easily solve the equation above with respect to incident photon energy: | ||
| − | <math>T_{\gamma} = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D E_n}{2\ (m_D - E_n + | + | <math>T_{\gamma} = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D E_n}{2\ (m_D - E_n)} |
| + | = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D (T_n+m_n)}{2\ (m_D - (T_n+m_n))} </math> | ||
| − | + | For non-relativistic neutrons <math>T_n \ll m_n = 939.5\ MeV</math> and the formula above is become: | |
| − | |||
| − | For non-relativistic neutrons <math>T_n \ll m_n = 939.5\ MeV</math> | ||
<math>T_{\gamma} = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D m_n + 2\ m_D T_n}{2\ (m_D - m_n)} </math> | <math>T_{\gamma} = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D m_n + 2\ m_D T_n}{2\ (m_D - m_n)} </math> | ||
| − | Substituting the corresponding masses, we get finally | + | Substituting the corresponding masses, we get finally: |
| − | <math>T_{\gamma}\ [MeV] = 2.003\ T_n\ [MeV] + 1. | + | <math>T_{\gamma}\ [MeV] = 2.003\ T_n\ [MeV] + 1.715\ [MeV]\ \ \ \ [1]</math> |
and visa versa: | and visa versa: | ||
| − | <math>T_n\ [MeV] = 0.499\ T_{\gamma}\ [MeV] - 0. | + | <math>T_n\ [MeV] = 0.499\cdot T_{\gamma}\ [MeV] - 0.856\ [MeV]\ \ \ \ [2]</math> |
| + | |||
| + | |||
| + | Here I derived the formula [2] just inversing the formula [1]. I can as well start from exact solution above, solve this equation with respect to neutron energy, do the non-relativistic approximation and get exactly the same formula [2]. But anyway we ended up with two useful non-relativistic formulas we can analyze now: | ||
| + | |||
| + | |||
| + | 1) from formula [1] above we can predict the threshold of <math>^2D(\gamma, n)</math> reaction in <math>\Theta_n = 90^o</math> direction: | ||
| + | <math>E_{\gamma} = 1.715\ MeV</math> | ||
| + | comment: it's not true because by momentum conservation there are no neutron with zero kinetic energy. | ||
| − | + | 2) from formula [1] above we can predict the incident photon energy based on the detected neutron energy (neutron polarimeter). | |
| + | 3) from formula [2] above we can predict the detected neutron energy based on the incident photon energy. | ||
| − | + | - for the incident photons up to <math>25\ MeV</math> we can detect neutrons up to <math>11.62\ MeV</math> | |
| − | <math> | + | - for the incident photons up to <math>44\ MeV</math> we can detect neutrons up to <math>21.10\ MeV</math> |
| − | + | 4) we can do the error calculations. | |
| + | |||
| + | =Example of error calculation= | ||
| + | |||
| + | ==simple error calculation== | ||
| + | |||
| + | Say, we have, 10 MeV neutron with uncertainty 1 MeV, | ||
| + | the corresponding uncertainly for photons energy is: | ||
| − | + | <math> \delta T_{\gamma} = 2.003\ \delta T_n = 2.003\times 1\ MeV = 2.003\ MeV </math> | |
| − | + | ==photon kinetic energy error <math>\delta T_{\gamma}</math> as function of TOF uncertainty <math>\delta t</math>== | |
| − | + | In the calculations below I attempted to predict the uncertainty in photons energy based on uncertainty in neutrons time of flight. | |
| − | |||
| + | The neutron kinetic energy as function of time of flight is: | ||
| − | + | <math>T_n = m_n (\gamma - 1) = m_n\left[ \frac{1}{\sqrt{1-\left(\frac{l}{c\ t}\right)^2}} - 1 \right]</math> | |
| − | + | By taking derivative of the expression above we can find the relative error for neutron energy: | |
| − | + | <math>\delta T_n \left(\delta t\right) = -\ \frac{m\ l^2}{\left(1-\left(\frac{l}{c\ t}\right)^2\right)^{3/2}c^2 t^3} \cdot \delta t</math> | |
| − | + | In that formula for <math>\delta T_n</math> we need to know the neutron time of flight which is: | |
| − | + | <math>t:=\frac{l}{c\ \beta_n} = \frac{l}{c\ (p_n/E_n)} = | |
| + | \frac{l\ (T_n + m_n)}{c\sqrt{T_n^2+2m_nT_n}}</math> | ||
| − | + | And now we can calculate the relative error for photon energy using the formula derived before: | |
| − | + | <math>\delta T_{\gamma} = 2.003\ \delta T_n</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
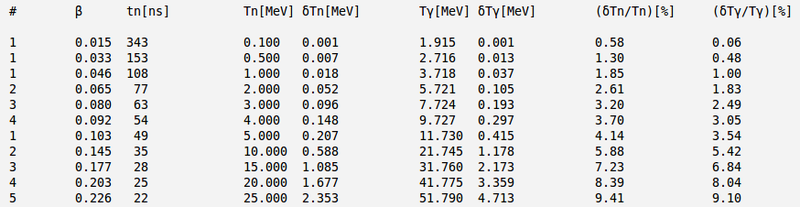
| − | + | Say, the detector is 1.5 m away and neutron's time of flight uncertainty is: | |
| − | = | + | <math>\delta t = 1\ ns</math> |
| − | + | And below are y numerical calculations and plot with error bars: | |
| − | |||
| − | + | [[File:table_1ns.png | 800 px]] | |
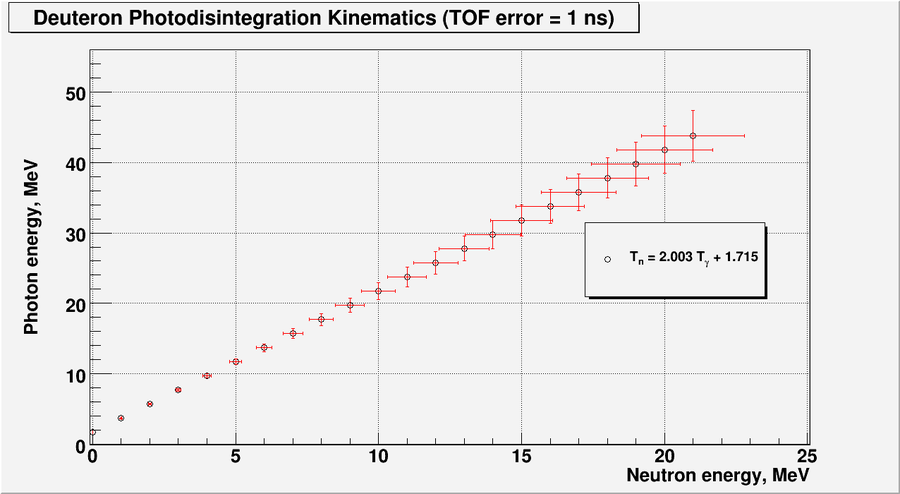
| − | + | And in the plot below I have overlay my error calculations using the formulas above: | |
| − | + | [[File:Tgamma_1ns_01.png | 900 px]] | |
| − | |||
| − | |||
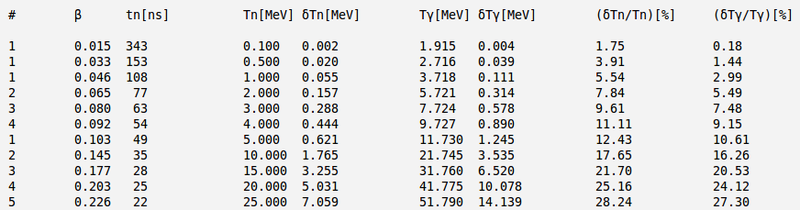
| − | + | Now say, the detector is 1.5 m away and neutron's time of flight uncertainty is: | |
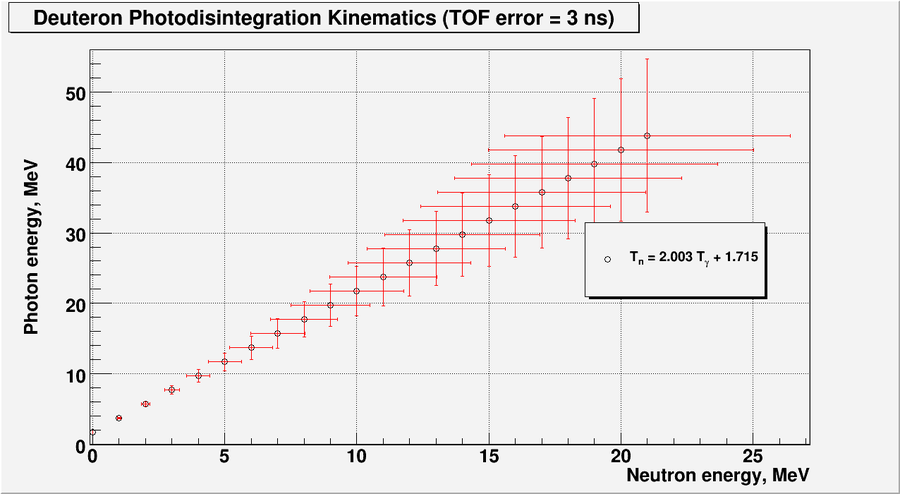
| − | <math> | + | <math>\delta t = 3\ ns</math> |
| + | [[File:table_3ns.png | 800 px]] | ||
| − | + | [[File:Tgamma_3ns_01.png | 900 px]] | |
| − | + | =<math>\Theta</math> dependence= | |
| − | |||
| + | Starting from general kinematic relations: | ||
| − | + | <math> m_p^2 = m_D^2 + m_n^2 + 2T_{\gamma}\cdot m_D - 2m_D\cdot E_n - 2\left( T_{\gamma}E_n - T_{\gamma}p_n\cos\Theta_n\right) </math> | |
| + | we can solve the equation above with respect to <math>T_{\gamma}</math> as function of neutron energy <math>T_n</math> and neutron angle <math>\Theta_n</math> | ||
| + | |||
| + | <math>T_{\gamma} = \frac{m_p^2-m_n^2-m_D^2+2m_D E_n}{2(m_D-E_n-p_n\cos\Theta_n)}</math> | ||
| − | + | and using | |
| + | <math>E_n = T_n+m_n</math> | ||
| + | <math>p_n = \sqrt{E_n^2-m_n^2} = \sqrt{T_n^2+2T_n m_n}</math> | ||
| − | + | finally | |
| − | <math>\ | + | <math>T_{\gamma} = \frac{m_p^2-m_n^2-m_D^2+2m_D (T_n+m_n)}{2\left(m_D-m_n-T_n-\sqrt{T_n^2+2T_n m_n}\cos\Theta_n\right)}</math> |
| − | |||
| − | |||
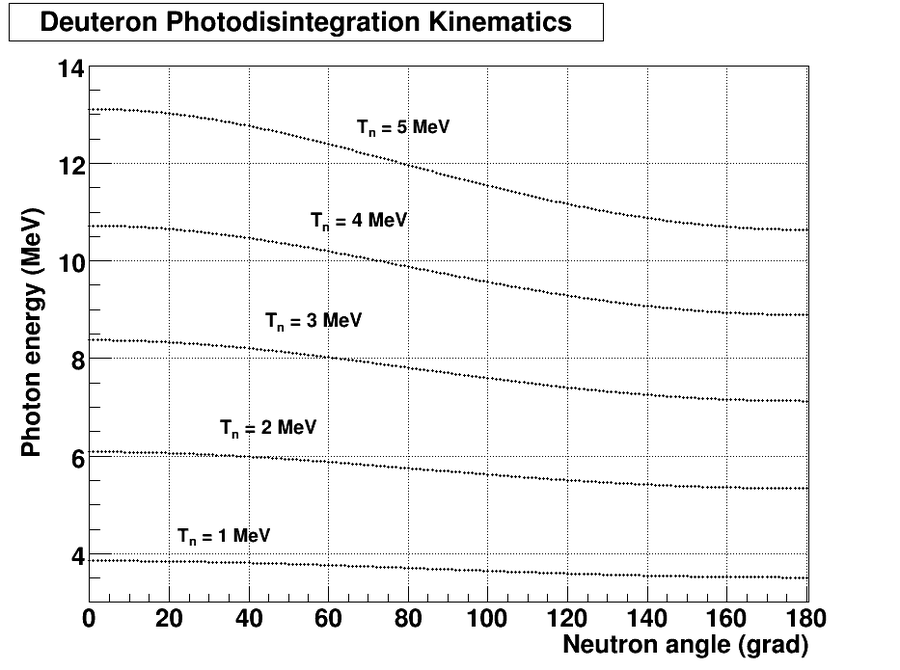
| − | + | Let's do some plots using the equation derived above. Below is presented the photon energy as function of neutron angle for several values of neutron energy: | |
| − | |||
| + | [[File:Tgamma_angle.png | 900 px]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
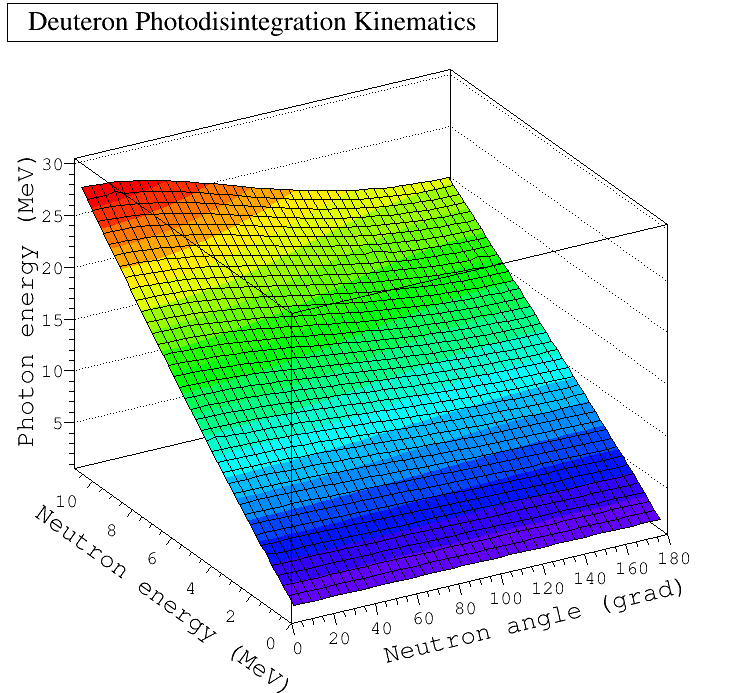
| + | And below are the photon energy as function of neutron angle and neutron energy: | ||
| + | [[File:Tgamma_3D_01.png | 900 px]] | ||
[http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | [http://wiki.iac.isu.edu/index.php/PhotoFission_with_Polarized_Photons_from_HRRL Go Back] | ||
Latest revision as of 05:17, 27 February 2013
Four-vector Algebra
Consider two body reaction :
Write down four-momentum vectors before and after reaction:
Now apply the law of conservation of four-momentum vectors:
Squaring both side of equation above and using the four-momentum invariants we have:
Detector located at case
Detector is located at , and the formula above is simplified:
We can easily solve the equation above with respect to incident photon energy:
For non-relativistic neutrons and the formula above is become:
Substituting the corresponding masses, we get finally:
and visa versa:
Here I derived the formula [2] just inversing the formula [1]. I can as well start from exact solution above, solve this equation with respect to neutron energy, do the non-relativistic approximation and get exactly the same formula [2]. But anyway we ended up with two useful non-relativistic formulas we can analyze now:
1) from formula [1] above we can predict the threshold of reaction in direction:
comment: it's not true because by momentum conservation there are no neutron with zero kinetic energy.
2) from formula [1] above we can predict the incident photon energy based on the detected neutron energy (neutron polarimeter).
3) from formula [2] above we can predict the detected neutron energy based on the incident photon energy.
- for the incident photons up to we can detect neutrons up to
- for the incident photons up to we can detect neutrons up to
4) we can do the error calculations.
Example of error calculation
simple error calculation
Say, we have, 10 MeV neutron with uncertainty 1 MeV, the corresponding uncertainly for photons energy is:
photon kinetic energy error as function of TOF uncertainty
In the calculations below I attempted to predict the uncertainty in photons energy based on uncertainty in neutrons time of flight.
The neutron kinetic energy as function of time of flight is:
By taking derivative of the expression above we can find the relative error for neutron energy:
In that formula for we need to know the neutron time of flight which is:
And now we can calculate the relative error for photon energy using the formula derived before:
Say, the detector is 1.5 m away and neutron's time of flight uncertainty is:
And below are y numerical calculations and plot with error bars:
And in the plot below I have overlay my error calculations using the formulas above:
Now say, the detector is 1.5 m away and neutron's time of flight uncertainty is:
dependence
Starting from general kinematic relations:
we can solve the equation above with respect to as function of neutron energy and neutron angle
and using
finally
Let's do some plots using the equation derived above. Below is presented the photon energy as function of neutron angle for several values of neutron energy:
And below are the photon energy as function of neutron angle and neutron energy: