Neutron Emission
Radioactivity and Neutron Emission
Radioactive material may emit neutrons, photons, electrons or alpha (ionized He-3) particles and may be either naturally occurring (intrinsic source) or manmade. The particles are emitted as the nuclei in the material transition from an excited state to the ground state.
Emitted neutron are classified into four types depending on their energy, each type has an energy range which may change from one reference to another. The following table shows the types of neutrons, their energy range, and common materials used for detecting them in that range.
| Neutron Type | Energy Range | Common detective material(s) |
| Ultracold Neutrons | less than 2*10^-7 | He-3 |
| Very Cold Neutrons | 2*10^-7eV =< K.E <= 5*10^-5 eV | He-3 |
| Cold Neutrons | 5*10^-5 eV =< K.E. =< 0.025 eV | He-3 |
| Thermal Neutrons | K.E ~_ 0.025 eV | Be-4, Li-6 |
| Epithermal Neutrons | 1 eV =< K.E =< 0.1 keV | U-235 |
| Intermediate Neutrons | 1 keV =< K.E =< 0.1 MeV | U-235 |
| Fast Neutrons | K.E > 0.1 MeV | U-233, U-238, Th-232 |
The table below shows radioactive nuclei and their half lives that mainly emit neutrons by spontaneous fission.
| Nuclide | Fission | -decay | Neutron/sec.gram |
| years | years | ||
| years | years | ||
| years | years | ||
| years | years | ||
| years | years | ||
| 66 years | 2.65 years |
In addition to the natural sources, they are industrial neutron sources is another neutron source (extrinsic). They are many ways to produce extrinsic neutron sources, using particle accelerators, Van de Graaff electrostatic accelerator, or by nuclear reactor. In case of using a particle accelerator, photon activation is one of the methods to produce this type of sources by carefully choosing an appropriate target.
When Van de Graaff accelerator is used, it projects a deuteron or a proton toward the target to produce neutrons, for example:
d ()n + 1.27 MeV
d ()n + 4.36 MeV
d ()n - 1.65 MeV <ref name=Ruess08 />
The nuclear reactor is another rich environment for many radioactive isotopes that are produced by a neutron fission, a neutron activation, or other processes such as .
It is noticed that most probable process for U -233 as neutron source is by induced neutron fission. One of the ways to look at U-233 nucleus is by analyzing the parameters that determine the neutron fission cross section such as: the fission barrier energy, activation energy, and binding energy. the following table shows the calculated values of these parameters in MeV unit <ref name = "Hyde" />:
| Nuclide | Fission Barrier | Activation Energy | Neutron Binding Energy | |
| 6.0 | 5.1 | 6.8 | 1.7 |
The table shows a positive difference between the fission barrier and the neutron binding energy which indicates that the fission cross section value for slow neutron >1 <ref name = "Hyde" />, also U-233 fission barrier is 6 MeV which made it high enough to avoid any spontaneous fission events. Those calculations qualify U-233 to be a target for induced neutrons, specifically for fast neutrons as will be shown in the next section.
Neutron Induced Fission of U-233 Cross Section
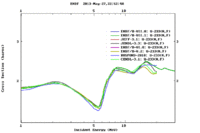
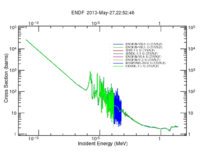
The definition of neutron induced fission cross section is the probability of occurrence of a fission interaction by an incident neutron that has a defined energy. Actinides and lanthanides generally have high fission cross sections compared to those of the rest of periodic table elements; for instance, U-235 has a high fission cross section for thermal neutrons, U-238 has a fission cross section for fast neutrons in barns, the same U-233 has a fission cross section in barns for almost all neutron energy range that starts with thermal neutron and ends with fast neutrons up to more than 30 MeV as shown in the following figure.
Also U-233 has neutron resonance peaks, most of them appear when the neutron energy is between 10 eV and less than 1 MeV. According to fission cross section categories, U-233 belongs a fission cross section category number 2 that describes the behavior of fissile nuclei that have a high fission cross section for thermal neutrons followed by plateau in fast neutron region that may drop 1 MeV around 5-7 MeV, then increase again for higher neutron energy. The drop indicates to a lower energy threshold for emitting another neutron from U-233 nucleus. Unfortunately, there is not a mathematical model that can describe resonances peaks and energy threshold over all the neutron energy range, but some models match the experimental cross section values only in a specific range of neutron energy. <ref name = "Hyde"/>
Induced fission cross section Plots are important to determine interaction rate of neutrons with the fissile thin films, they are generally two types of cross sections: microscopic and macroscopic fission cross sections, the microscopic cross section defined the effective area for a single nucleus for an interaction. The macroscopic cross section determines the probability of a neutron to interact when it travels a unit distance in a macroscopic material, its unit is (which is the reciprocal of mean free path), it is defined mathematically in terms of the microscopic cross section by:<ref name="Knief"> Knief R.A., (1992). Nuclear Engineering: Theory and Technology of Commercial Nuclear Power. 2nd ed. e.g. England: Hemisphere Publishing Corporation. </ref>:
Where is the macroscopic cross section and is the microscopic cross section , n is the material (target) atomic density .
When a neutron flux () interacts with a material of thickness x, the flux exponentially attenuates inside the material as shown by the formula:
so,
The microscopic cross section of the material is:
Where is the number incident particle per uni area per unit time, dN is the average number of particles per unit time that interacted per unit solid angle, and is the solid angle.
Since the cross section has an area unit (barn), some authors define this quantity as the area to which the particle is exposed to make an interaction. <ref name="Ahmed">Syed Ahmed, Physics and Engineering of Radiation Detection (Academic Press 2007) </ref> The cross section values are represented as a function of energy that gives the value of the cross section for each energy value and shows the resonance peaks. A theoretical description of the neutron fission cross section curve over all an energy range is not available, but statistically it is possible to evaluate the parameters for an assumption that describes part of the cross section curve within a determined error.<ref name="Hyde"/>
<references/>