Lab 6 TF EIM

Lab 6 Pulses and RC Filters

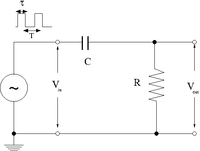
Differentiator

1.)Construct the circuit below selecting an RC combination such that RC [math]\lt 10^{-4} [/math] s

2.) Adjust the pulse generator to output square pulses which at [math]\tau \approx[/math] RC/10.

3.)Measure[math] V_{in}[/math] and [math]V_{out}[/math]. Sketch a picture comparing[math] V_{out}[/math] and [math]V_{in}[/math]. ( 5 pnts.)

4.) Change the pulse width such that [math]\tau=[/math]RC

5.)Measure[math] V_{in}[/math] and [math]V_{out}[/math].Sketch a picture comparing[math] V_{out}[/math] and [math]V_{in}[/math].( 5 pnts.)

6.) Change the pulse width such that [math] \tau[/math]=10 RC

7.)Measure [math]V_{in}[/math] and [math]V_{out}[/math].Sketch a picture comparing[math] V_{out}[/math] and [math]V_{in}[/math].( 5 pnts.)

Questions

1.) What happens if the amplitude of [math]V_{in}[/math] is doubled.( 5 pnts.)

2.) What happens if R is doubled and C is halved?( 5 pnts.)

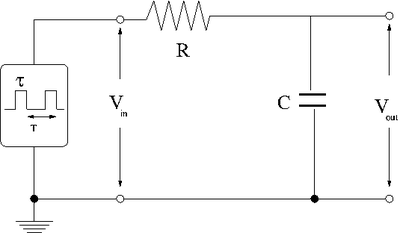
Integrator

Now repeat the above experiment with the resistor and capacitor swapped to form the low pass circuit below.

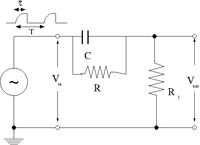
Pulse Sharpener

The goal of this section is to demonstrate how well the circuit below can sharpen an input pulse

1.) The first step is to create an input pulse which is rounded, similar to the output of the integrator circuit when RC = 10 [math]\tau[/math]. You can do this using a capacitor shorted across the output of the pulse generator. This will essential be coupled to the input impedance of the pulse generator and form a low pass circuit.

As a result the input voltage is given as

[math]V_{in} = V_0 \left ( 1 - e^{-t/\tau}\right )[/math]

where

[math]\tau=R_{out} C_{out}[/math]

[math]R_{out}[/math] = impedance of the function generator at output which produces V_{in}

[math]C_{out}[/math] = capacitor shorting the function generator output to ground (not shown in the above picture)

2.) The output should be given by

[math]V_{out} = V_0^{\prime} \left ( 1 - e^{-t/\tau^{\prime}}\right )[/math]

where

[math]\tau^{\prime} =\left ( \frac{R_1 R}{R_1+ R}\right )C_1[/math]

3.) Make measurements of the rise time [math]\tau[/math] and [math]\tau^{\prime}[/math]. The rise time is defined as the time it takes the pulse to go from 0 to [math](1-e^{-1})[/math] = 0.63 of its max value.( 5 pnts.)

4.) Compare the measurement of [math]\tau^{\prime}[/math] to what you expected based on your measured values of [math]C_1[/math], [math]R_1[/math] and[math] R[/math].( 15 pnts.)

Questions

1.) Qualitatify, why is [math]\tau^{\prime} \lt \tau[/math]?( 10 pnts.)

2.) How is [math]V_{out}[/math] worse than [math]V_{in}[/math]( 10 pnts.)

Forest_Electronic_Instrumentation_and_Measurement