Kicker Magnets
Kicker Magnet - Theoretical Part
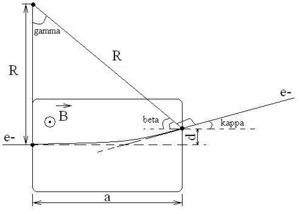
Field needed to bend 44 MeV electrons 0.47 degrees
, ,
- general expression for B-field.
If then and our B-field becomes:
for the coils under consideration. Hence, the B-field needed is:
Magnetic Field Produced by Coils
Assuming the coils we are using are in a solenoidal shape, we have:
which gives us
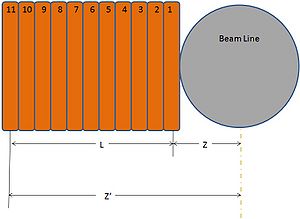
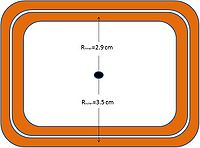
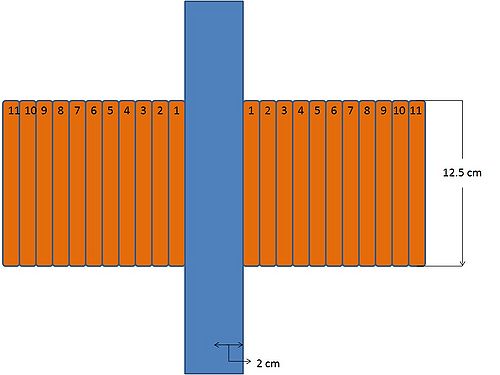
These coils consist of 11 turns of which each turn is two deep. Furthermore, we have an inner and an outer radius . The above magnetic field can be found for both the inner and the outer layer of the coil for each turn of the coil. The maximum current these coils can handle (according to IAC personnel) is 100 Amps. Listed below is the data calculated for 100 Amps.
| Turn Number | Distance from Beam | B-Field (inner) | B-Field (outer) |
| 1 | 2 cm | 12.12 G | 11.78 G |
| 2 | 2.65 cm | 8.74 G | 9.12 G |
| 3 | 3.3 cm | 6.25 G | 6.93 G |
| 4 | 3.95 cm | 4.5 G | 5.25 G |
| 5 | 4.6 cm | 3.3 G | 4 G |
| 6 | 5.25 cm | 2.46 G | 3.07 G |
| 7 | 5.9 cm | 1.86 G | 2.39 G |
| 8 | 6.55 cm | 1.44 G | 1.88 G |
| 9 | 7.2 cm | 1.33 G | 1.5 G |
| 10 | 7.85 cm | 0.90 G | 1.22 G |
| 11 | 9 cm | 0.73 G | 0.99 G |
Adding the inner and outer fields gives a combined field of 92 G per coil. If we used two coils, one on each side of the beam line we would have a field of 183 G, which is above the needed field to bend electron 0.47 degrees. But, by knowing the field we need, 96 G, we can reverse calculate the current needed to produce 96 G by these coils.
Conclusion
It is found that if we supplied 52 Amps to a pair of these coils we would get a magnetic field in the beam line of 0.0096 T, which is the field required to bend an electron 0.47 degrees.
Kicker Magnet - Experimental Part
Setup and Data
An experiment was done to see how the theoretical calculations compare to the experimental data. Two of the coils described above were used. The chilled water system in the experimental hall of the HRRL was used to circulate water through the coils. The coils were connected to a power supply that is capable of producing 300 Amps and 100 Volts. A schematic of the setup is shown below.
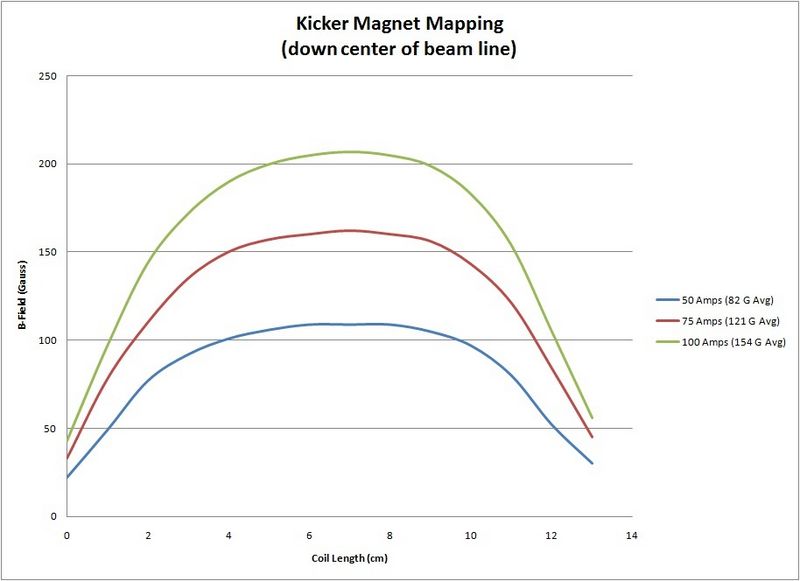
Data was obtained for three different currents, 50 Amps, 75 Amps, and 100 Amps. The data measured is listed below.
| Length of Coils (cm) | B-Field 50 Amps (G) | B-Field 75 Amps (G) | B-Field 100 Amps (G) |
| 0 | 22 | 33 | 43 |
| 1 | 49 | 78 | 97 |
| 2 | 77 | 110 | 144 |
| 3 | 92 | 135 | 172 |
| 4 | 101 | 150 | 190 |
| 5 | 106 | 157 | 200 |
| 6 | 109 | 160 | 205 |
| 7 | 109 | 162 | 207 |
| 8 | 109 | 160 | 205 |
| 9 | 105 | 156 | 199 |
| 10 | 97 | 143 | 183 |
| 11 | 80 | 121 | 154 |
| 12 | 52 | 84 | 105 |
| 13 | 30 | 45 | 56 |
Summary
As can be seen from comparing the theoretical to the experimental data, the values are pretty close. The assumption of the coils being circular solenoids is one possibility of the discrepancy. Furthermore, it is determined that about 60 Amps is needed to bend a 44 MeV electron 0.47 degrees.