July, 6, 2007 Investigations of Geometry Influence on the Fission Fragments Behaviour
1. Theoretical Calculations
Relativistic charged particles lose energy in matter primarily by ionization. The mean rate of energy loss is given by the Bethe_Bloch equation,
- =K[ - - ]
= 0.307075 MeV
=61 keV
=0.033
For example, for incident particle Ce-140 and target U-238, we have following results for energy loss
Density of Uranium is 19.1 [1]
- = = 2.66
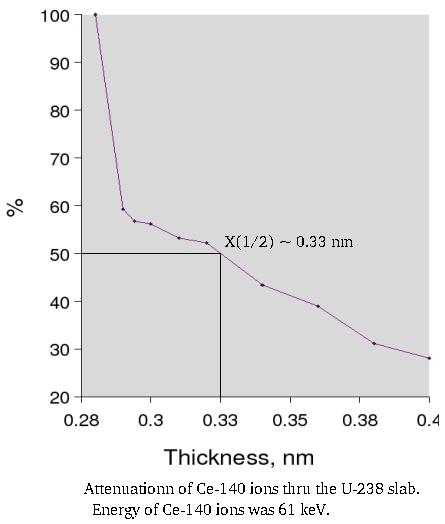
The half length is the distance needed to reduce the intensity in half
= nm = 0.0115 nm
Time t= = nsec
2. Simulation
(i) Simulated half-length for totally ionized unexited Ce-140 (A=140, Z=58, Q=58, E'=0) having energy 61 keV propagated thru the U-238 target:
Half-length:
Time needed to the Ce-140 ion to pass half-length:
Time =
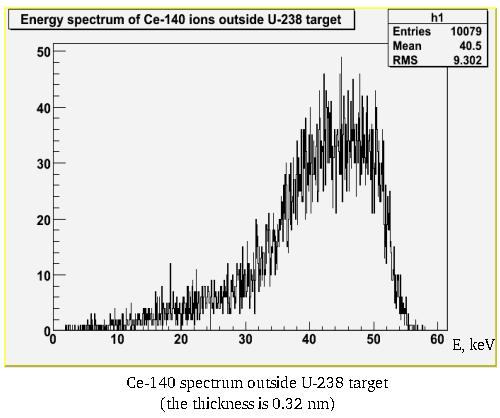
(ii) Energy spectrum of Ce-140 ions (E = 61 keV). Number of incident ions was 20,000: