Integrated asymmetry

Go Back

Integrated asymmetry calculation

[math]Asymm^{detA,detC} = \frac {\left(\frac{N_{up}^{D_2O}}{W_{up}^{D_2O}}-\frac{N_{up}^{H_2O}}{W_{up}^{H_2O}}\right) - \left(\frac{N_{side}^{D_2O}}{W_{sided}^{D_2O}}-\frac{N_{side}^{H_2O}}{W_{sd}^{H_2O}}\right)} {\left(\frac{N_{up}^{D_2O}}{W_{up}^{D_2O}}-\frac{N_{up}^{H_2O}}{W_{up}^{H_2O}}\right) + \left(\frac{N_{side}^{D_2O}}{W_{sd}^{D_2O}}-\frac{N_{sided}^{H_2O}}{W_{sd}^{H_2O}}\right)} [/math]

where

[math]N_{k}^{m}=\sum_{ii=min}^{max}{count(ii)};[/math]   total number of neutrons detected, k = [Up,Side], m = [D2O, H2O]

[math]W_{k}^{m};[/math]  weighted (NaI, Ref) coefficient, k = [Up,Side], m = [D2O, H2O] 

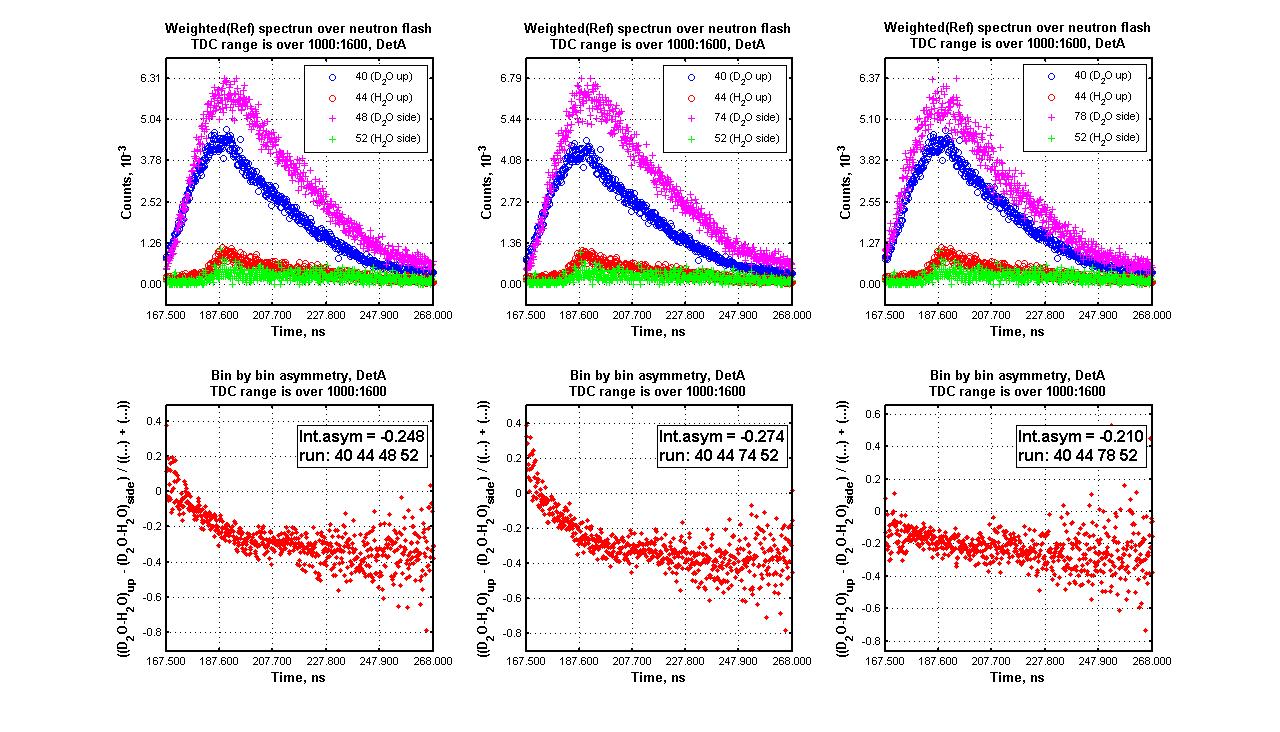
• For detector A summation is over [1000:1600] bin numbers
  
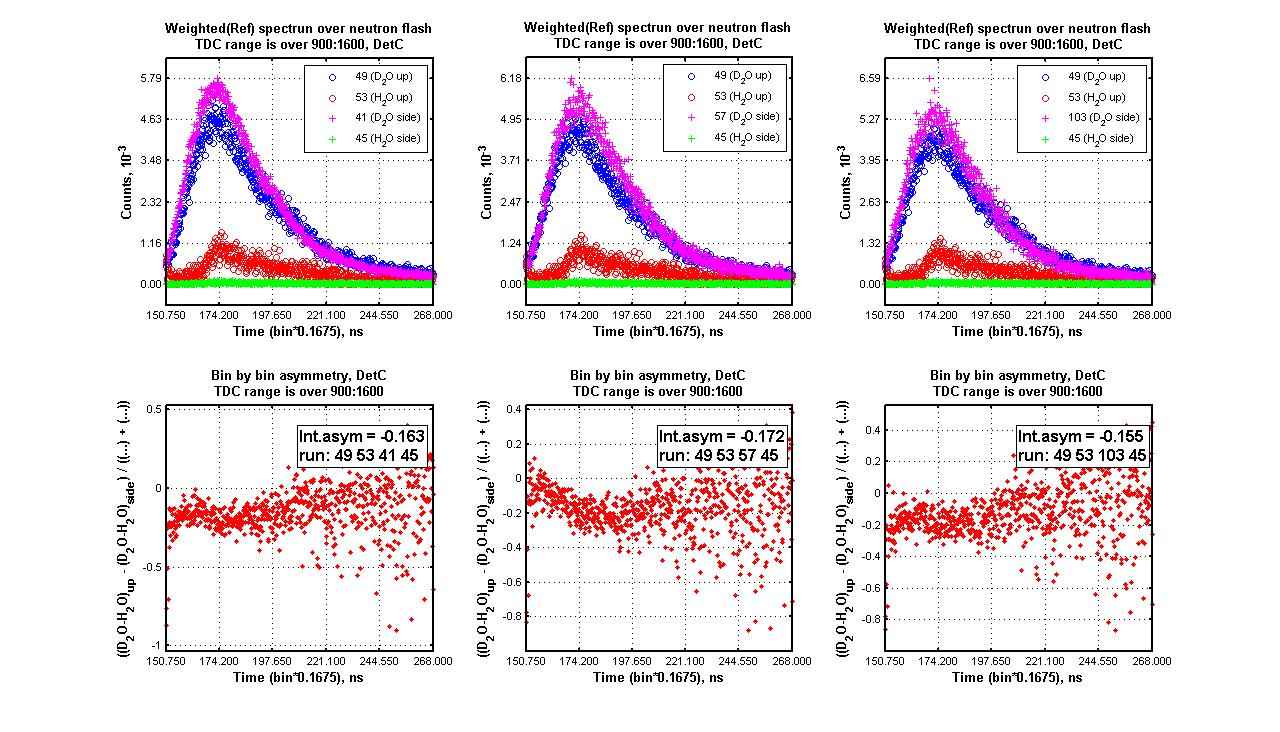
• For detector C summation is over [900:1600] bin numbers
  
  

Error calculation

[math]\delta (Asymm) = \sqrt{\sum_{k=up}^{side}\ \sum_{m=D_2O}^{H_2O} \left[\left(\frac{\partial A}{\partial N_{k}^{m}}\delta N_{k}^{m}\right)^2 + \left(\frac{\partial A}{\partial W_{k}^{m}}\delta W_{k}^{m}\right)^2\right]}[/math]

What about

[math]\frac{\partial A}{\partial N_{k}^{m}}\frac{\partial A}{\partial W_{k}^{m}}[/math]

what is <math>\sqrt{up}</math> ?  
Does <math>\sqrt{up}</math> = number of counts in in the detector 
up spectrum as suggested above?  Why not use <math>N_{up}</math> as variable.  
If distribution is Binomial (detector yes/no) then width of distribution is 
<math>1.265\sqrt{N}</math> = 2 times e error.  
Relative error = <math>\frac{error}{Ave} = \frac{0.6325 \sqrt{N}}{N/2}</math>

If you are measuring total number of neutrons detected then you will have binomial if you 
break up the time spectrum into bins and don't integrate then probability distribution
is combination of detection probability and time measurement probability.

If we take:
[math]\delta N_{k}^{m} = \sqrt{N_{k}^{m}}[/math]
[math]\delta W_{k}^{m} = \sqrt{N_{k}^{m}}[/math]

then
[math]\delta (Asymm) = \sqrt{ \left(\frac{(+)-(-)}{(+)^2}\right)^2\left( \frac{N_{up}^{D_2O}}{(W_{up}^{D_2O})^2}+\frac{(N_{up}^{D_2O})^2}{W_{up}^{D_2O}} +\frac{N_{up}^{H_2O}}{(W_{up}^{H_2O})^2}+\frac{(N_{up}^{H_2O})^2}{W_{up}^{H_2O}}\right)+ \left(\frac{(+)+(-)}{(+)^2}\right)^2\left( \frac{N_{sd}^{D_2O}}{(W_{sd}^{D_2O})^2}+\frac{(N_{sd}^{D_2O})^2}{W_{sd}^{D_2O}} +\frac{N_{sd}^{H_2O}}{(W_{sd}^{H_2O})^2}+\frac{(N_{sd}^{H_2O})^2}{W_{sd}^{H_2O}}\right)}[/math]

where
[math](-)=\left[ \left(\frac{N_{up}^{D_2O}}{W_{up}^{D_2O}}-\frac{N_{up}^{H_2O}}{W_{up}^{H_2O}}\right) -\left(\frac{N_{sd}^{D_2O}}{W_{sd}^{D_2O}}-\frac{N_{sd}^{H_2O}}{W_{sd}^{H_2O}}\right)\right][/math]

[math](-)=\left[ \left(\frac{N_{up}^{D_2O}}{W_{up}^{D_2O}}-\frac{N_{up}^{H_2O}}{W_{up}^{H_2O}}\right) +\left(\frac{N_{sd}^{D_2O}}{W_{sd}^{D_2O}}-\frac{N_{sd}^{H_2O}}{W_{sd}^{H_2O}}\right)\right][/math]

Cases was analysed

Det A (was analized all possible combination):

D2O Up,   files# [40,56,102,108,205,210,230];

H2O Up,   files# [44];

D2O Side, files# [48,74,78,82,86,90,94,146,190,225,235];

H2O Side, files# [52];

Det C (was analized all possible combination):

D2O Up,   files# [49,75,79,83,87,91,95,147,191,226,236];

H2O Up,   files# [53];

D2O Side, files# [41,57,103,107,206,211,231];

H2O Side, files# [45];

Weighted coefficients was used

(File:Weight coeff.pdf)

Results

Table 1: Det A, weighted with [math]{\color{Red}NaI \ detector}[/math]

Table 2: Det C, weighted with [math]{\color{Red}NaI \ detector}[/math]

Table 3: Det A, weighted with [math]{\color{Red}Ref \ detector}[/math]

Table 4: Det C, weighted with [math]{\color{Red}Ref \ detector}[/math]

(File:Asymm table.pdf)

Example of bin by bin asymmetry

Change the X-axis to nanosecond or neutron energy (TF). A:Have done.

Go Back