HRRL radiation tests

From New IAC Wiki
Jump to navigation Jump to search

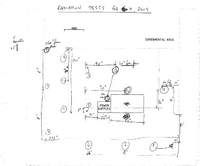
Building a new positron beamline in the HRRL cell might require moving the linac itself. R adiation levels were measured on Feb 4, 2009 by M. Balzer and G. Stancari to determine the impact of repositioning the HRRL RF cavity in the accelerator room.

The HRRL was used to accelerate electrons to a 15 MeV beam energy, 20 mA peak current, 1 kHz repetition rate, and 30 ns pulse width. Five OSL dosimeters (For Details on OSL dosimeter, look [[1]]) were placed at each of 15 locations within the cell identified in the sketch below.

Dosimeter-locations-20090204.png

Media:dosimeter-locations-20090204.pdf

Readings in mrad are reported in the following table. They were taken before exposure (first column) and after a couple of minutes of machine tuning (second column). Readings in the third column were taken 94 minutes after the second reading. During these 94 minutes, the machine was running with the settings mentioned above.

Exposure-measurements-20090204.png

Media:exposure-measurements-20090204.pdf

Dose rates in mrad/hr at each of the 15 locations can be estimated by subtracting column 2 from column 3, averaging over the 5 dosimeters, and multiplying the result by (60 min/hr) / (94 min). RMS spreads refer to variations within each group of 5.

Location Dose rate RMS spread
(mrad/hr) (mrad/hr)
1 9 4
2 396 57
3 7940 204
4 2831 117
5 4408 373
6 29339 3332
7 72517 687
8 36507 4746
9 5 5
10 37 4
11 164 40
12 2734 313
13 5828 120
14 7793 2579
15 62431 27155


OSL dosimeters

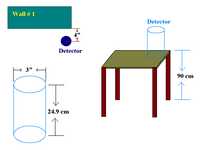
Dosimeters are placed approximately 1-m off the floor. Large face of the dosimeters were facing HRRL.

Diameter of a dosimeter is measured as:

d = 7.4 mm, 7.6 mm, 7.5 mm, 7.3 mm, 7.3 mm, 7.4 mm, 7.6 mm.

so,

d = 7.44 [math]\pm [/math] 0.13 mm.

OSL dosimeters.jpg

Experimental Cell Dose Measurement with HRRL

This experiment is done on 5/17/2010, at 10:00 am.


Experiment Setup.png


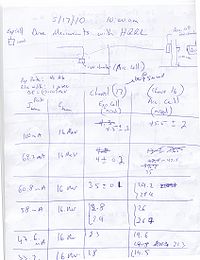
Dr. Khalid Chouffani wrote the note. Here is photocopy of his note:

page #1

Note P1.jpg

Note P1 2.jpg


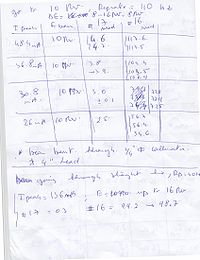
page #2

Note P2.jpg


Detector Used on Channel 16

Channal 16 Detector 1.jpg

Channal 16 Detector 2.jpg

Channal 16 Detector 3.jpg

Link to detector information from producer: [2]

For more detailed information go to: ludlums_Gamma_Area_Monitor_moedl_45-9

16 MeV Beam Energy

Experimental cell measurement with HRRL.

Conditions are:

Rep rate: 40 Hz

Pulse width: 1 [math]\mu sec[/math]

[math]\Delta[/math]E=(10-17) MeV

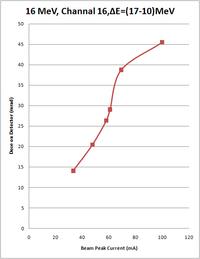
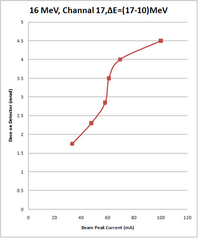
Peak current of beam (mA) Energy of beam (MeV) Measurement on Channel 17, Experimental Cell (mrad) Measurement on Channel 16, Accelerator cell (mrad) Ratio: Chan16/Chan17
100 16 4.5 [math]\pm [/math] 0.2 45.5 [math]\pm [/math] 2 10.1
69.2 16 4 [math]\pm [/math] 0.2 35, 42.5 8.6
60.8 16 3.5 [math]\pm [/math] 0.1 29.2, 28.9 8.3
58.0 16 2.8, 2.9 26, 26.7 9.2
47.6 16 2.3 19.6, 21.3 8.9
33.2 16 1.8, 1.7 14.5, 14.0, 13.7 8.0

Beam bear through 1/4 inches diameter collimator with 4 inches lead.


16MeV Chan16.png


16MeV Chan17.png


Fit for Channel 16 at 16MeV

Order of the fit Fit equations Chi square p-value
1st order [math] Dose = (-2.305 \pm 0.095) + (0.511 \pm 0.01)*I_{peak} [/math] 22.38 0.00017

16 MeV Beam Energy

Conditions are:

Rep rate: 40 Hz

Peak current of beam (mA) Energy of beam (MeV) Measurement on Channel 17, Experimental Cell (mrad) Measurement on Channel 16, Accelerator cell (mrad)
136 16 0.3 99.2, 98.7

10 MeV Beam Energy

Conditions are:

Rep rate: 110 Hz

[math]\Delta[/math]E=(8-16) MeV

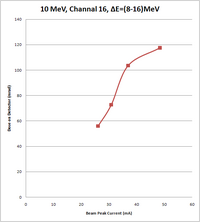
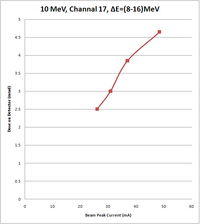
Peak current of beam (mA) Energy of beam (MeV) Measurement on Channel 17, Experimental Cell (mrad) Measurement on Channel 16, Accelerator cell (mrad) Ratio: Chan16/Chan17
48.4 10 4.6, 4.7 117.6, 117.5 25.28
36.8 10 3.8, 3.9 104.4, 103.5, 102.9 26.91
30.8 10 3.1 [math]\pm [/math] 0.1 72.8, 72.9, 72.5 23.46
26 10 2.5 56.7, 56.4, 54.6 22.27


10MeV Chan16.png


10MeV Chan17.png


Fit for channel 17 at 10 MeV

Order of the fit Fit equations Chi square p-value
1st order [math] Dose = (-0.039 \pm 0.066) + (0.1001 \pm 0.01)*I_{peak} [/math] 0.983 0.6117

Channel 17 Dose Estimation in New Position

Channel 17 is a dose measuring detector on in the HRRL experimental cell.

Calculation

1 rad = 0.01 J/Kg;

Assume that the position 13 at radiation test on Feb 4, 2009 by M. Balzer and G. Stancari will shift to detector position at corner on experiment that is done on 5/17/2010.

Radiation test on Feb 4, 2009 by M. Balzer and G. Stancari used OSL dosimeter.

The area of a OSL dosimeter is:

[math]A_{osl} = 55.3536 \pm 3.0 ~mm^{2} [/math]

Experimental Cell Dose Measurement with HRRL on 5/17/2010 used Ludlums Gamma Area Monitor moedl 45-9 for channel 16. Ludlums Gamma Area Monitor moedl 45-9 has dimension: 7.6 x 25.7 cm (3 x 10.1 in.) (Dia x L).

The area of a Ludlums Gamma Area Monitor moedl 45-9 is:

[math] A_{lgam}=195.32 ~cm^{2} [/math]

The ratio of detectors detecting area is:

[math]\frac{ A_{osl} } {A_{lgam}} = 352.9 \pm 19 [/math]

We assume 100% efficiency for both detectors, their detecting are ratio is their dose ratio.

So, for 15 MeV electron beam, at the corner where we had detector of channel 16, if we moved detector to new position, on the detector of Ludlums Gamma Area Monitor moedl 45-9 we would have dose rate of :

Dose [math] = (352.9 \pm 19) \times 5828 [/math] (mrad/hr)

[math] = 2056701.2 \pm 110 732[/math] (mrad/hr)

[math] = 571.3 \pm 31 [/math] (mrad/sec)

Above dose is created by electron beam of energy 15 MeV and 20 mA peak current.


According to the fit for Channel 16 at 16MeV, for 20 mA of peak current the dose should be:

[math] Dose = (-2.305 \pm 0.095) + (0.511 \pm 0.01)*I_{peak} = (-2.305 \pm 0.095) + (0.511 \pm 0.01)*20 = 1.96 \pm 0.27[/math] (mrad/)


According to the fit for Channel 17 at 10MeV, for 20 mA of peak current the dose should be:

[math] (-0.039 \pm 0.066) + (0.1001 \pm 0.01)*I_{peak} [/math]

The ratio,at 20 mA of peak current, of Channel 16 at 16MeV to Channel 17 at 10MeV is:

[math] \frac{7.915 \pm 0.30}{1.96 \pm 0.27} = 4.03 \pm 0.57 [/math]

Or, the ratio,at 20 mA of peak current, of Channel 17 at 10MeV to Channel 16 at 16MeV is:

[math] \frac{1.96 \pm 0.27}{7.915 \pm 0.30} = 0.248 \pm 0.035 [/math]


Assume proximately same dose rate for 15 MeV and 16 Mev electron beam, so dose rate channel 17 at 10 MeV electron beam is:

[math] \frac{(Dose~Chan17~10MeV)}{(Dose~Chan16~16MeV)} \times (Dose~Chan16~15MeV) \approx {Dose~Chan17~10MeV} [/math]

Which lead to Dose rate of channel 17 at 10 MeV electron and 20 mA peak current:

[math] (0.248 \pm 0.035) \times [/math] [math] 571.3 \pm 31 (mrad/sec) = 142\pm 21[/math]


New Radiation Test

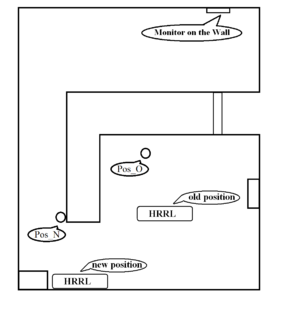
We plan to run another radiation experiment on HRRL. We will place a detector measure dose rate near the corner of wall1, call this position as "Pos_N" (for detector position at HRRL's New Position). We found equivalent position of Pos_A for old position of HRRL, call it "Pos_O" (for detector position at HRRL old Position). So, if we move HRRL from the old position to the new position, Pos_O will overlap with Pos_N.


New Old Relative Pos Detector.jpg


We want to run radiation tests on both Pos_O and Pos_N with same detector switching around.

When detector is at Pos_N, we will get dose rate at Pos_N ([math]D_{N}[/math]) and dose rate at monitor on the wall of experimental side [math]D_{MO} [/math]. From this we want to get ratio of two: 

                                    [math] R_{NM} = \frac{D_{MO}}{D_{N}} [/math]

When detector is at Pos_O (HRRL is still at old position), we will get the expecting dose rate of detector at Pos_N after moving HRRL to new position. Let's call this dose rate " [math] D_{O} [/math] ".

Then, the dose rate on monitor after moving HRRL to new position will be; 

                       [math] D_{MN}  = D_{O} \times R_{NM} = D_{O} \times \frac{D_{MO}}{D_{N}} [/math]


Run Plan

Parameters that we can play with are:

1) Rep rate (0-1000);

2) Electron Beam Energy (10,15 MeV);

3) Peak current of beam (20-100 mA).

We increase rap rate till we saturate detector, or we hit 900 Hz limit.

We don't have dipole any more, so we don't know exact energy we are operating. But, from previous measurements we know the relation of control voltage to the energy:


Control Voltage= 4.9 V [math]\Rightarrow[/math] E = 16 MeV

to

4.09 V [math]\Rightarrow[/math] E = 10 MeV

So, we just have 2 energy options, 10 and 16 MeV.

28 Jul 2010

channel 17: Monitor

channel 16: Pos_N and Pos_O.

Pulse width: full width half max is 150 ns.

Energy of beam (MeV) Peak current of beam (mA) Rap rate (Hz) Dose Rate on Pos_N [math]D_{N}[/math] (mrad) Dose Rate on Monitor [math]D_{MO} [/math] (mrad) Dose Rate on Pos_O [math] D_{O}[/math] (mrad)
10 40 40 3.6+-0.5 0 63+-2
10 40 100 0 25+-5
10 40 400 17.5+-0.5 0 855+-10
10 40 900 54+-5 0.1 no data


Energy of beam (MeV) Peak current of beam (mA) Rap rate (Hz) Dose Rate on Pos_N [math]D_{N}[/math] (mrad) Dose Rate on Monitor [math]D_{MO} [/math] (mrad) Dose Rate on Pos_O [math] D_{O}[/math] (mrad) Expected Dose Rate at Monitor after Moving the Cavity to New Position [math]D_{MN}[/math] [math] 1/R_{NM} = \frac{D_{N}}{D_{MO}} [/math]
16 40 40 30+-2 0.1 500 +- 5 1.7+-0.1 300
16 40 70 53+-2 0.2 800 +- 5 3.0+-0.1 265
16 40 900 135+-2 0.7 no data
16 40 500 79+-1 0.4 no data

29 Jul 2010

Shielding is changed from yesterday. I shielded very well.

channel 17: Monitor

channel 16: Pos_N and Pos_O.

Pulse width: full width half max is 150 ns.

Energy of beam (MeV) Peak current of beam (mA) Rap rate (Hz) Dose Rate on Pos_N [math]D_{N}[/math] (mrad) Dose Rate on Monitor [math]D_{MO} [/math] (mrad) Dose Rate on Pos_O [math] D_{O}[/math] (mrad)
10 40 40 0.2 0.0 3.8+-0.2
10 40 100 0.5 0.0 9+- 0.3
10 40 200 1.5+-0.1 0.0 16.8 +- 0.3
10 40 300 2.5+-0.1 0.0 26 +- 0.5
10 40 400 2.0+-0.1 0.0 37.5 +- 0.5
10 40 500 4.5+-0.1 0.0 49.3 +- 1
10 40 600 5.5+-0.1 0.0 75+-1.5
10 40 700 7.7+-0.1 0.0 83 +- 1.5
10 40 800 8.5+-0.1 0.0 110 +- 2
10 40 900 8.5+-0.5 0.0 129 +- 3



Energy of beam (MeV) Peak current of beam (mA) Rap rate (Hz) Dose Rate on Pos_N [math]D_{N}[/math] (mrad) Dose Rate on Monitor [math]D_{MO} [/math] (mrad) Dose Rate on Pos_O [math] D_{O}[/math] (mrad) Expected Dose Rate at Monitor after Moving the Cavity to New Position [math]D_{MN}[/math] [math] 1/R_{NM} = \frac{D_{N}}{D_{MO}} [/math]
16 40 40 1.7 +-0.1 0.0 17.7+-0.1
16 40 70 2.9 0.0 30.3 +- 0.1
16 40 100 4.0+- 0.1 0.0 43.1 +- 0.2
16 40 200 8.4+-0.2 0.0 87.5+-0.3
16 40 300 12.4+-0.1 0.0 131.0+-0.5
16 40 400 16.5+-0.1 0.1 173.3+-0.5 1.05+-0.01 165
16 40 500 20+-0.3 0.1 218+-1 1.09+-0.02 200
16 40 600 24.8+-0.2 0.15 260+-2 1.57+-0.02 165
16 40 700 28.8+-0.2 0.2 302+-2 2.10+-0.02 144
16 40 800 32.2+-0.1 0.2 350+-5 2.17+-0.03 161
16 40 900 36.1+-0.3 0.2 400+-5 2.22+-0.03 180.5



Energy of beam (MeV) Peak current of beam (mA) Rap rate (Hz) Dose Rate on Pos_N [math]D_{N}[/math] (mrad) Dose Rate on Monitor [math]D_{MO} [/math] (mrad) Dose Rate on Pos_O [math] D_{O}[/math] (mrad)
16 80 40 0.7 0.0 8.8+-0.1
16 80 70 1+-0.2 0.0 18.5+-0.2
16 80 100 2+-0.2 0.0 26+-0.5
16 80 200 5+-0.5 0.0 68+-2
16 80 300 5.5+-1 0.0 100+-5
16 80 400 6+-1 0.0 140+-10
16 80 500 7.5+-1 0.0 150+-20
16 80 600 8+-1 0.0 220+-20
16 80 700 11.5+-2 0.0 250+-20
16 80 800 17+-3 0.0 320+-30
16 80 900 19+-3 0.0 400+-30



Energy of beam (MeV) Peak current of beam (mA) Rap rate (Hz) Dose Rate on Pos_N [math]D_{N}[/math] (mrad) Dose Rate on Monitor [math]D_{MO} [/math] (mrad) Dose Rate on Pos_O [math] D_{O}[/math] (mrad)
16 20 40 0.2 0.0 2.5+-0.5
16 20 70 0.3 0.0 4+-0.5
16 20 100 0.3 0.0 5.5+-0.5
16 20 200 0.6 0.0 12+-1
16 20 300 1+-0.2 0.0 18+-2
16 20 400 1.2+-0.3 0.0 21+-2
16 20 500 1.4+-0.3 0.0 27+-3
16 20 600 1.8+-0.4 0.0 33+-3
16 20 700 2.0+-0.3 0.0 41+-3
16 20 800 2.2+-0.3 0.0 50+-5
16 20 900 2.5+-0.5 0.0 63+-5



Energy of beam (MeV) Peak current of beam (mA) Rap rate (Hz) Dose Rate on Pos_N [math]D_{N}[/math] (mrad) Dose Rate on Monitor [math]D_{MO} [/math] (mrad) Dose Rate on Pos_O [math] D_{O}[/math] (mrad)
16 40 40 0.3 0.0 4.5+-0.5
16 40 70 0.5 0.0 9.5+-1
16 40 100 0.6 0.0 13+-1
16 40 200 1.4 +-0.3 0.0 35+-2
16 40 300 1.7+-0.3 0.0 44.5+-2
16 40 400 2.5+-0.3 0.0 50+-2
16 40 500 3.0+-0.3 0.0 52.5+-3
16 40 600 3.4+-0.3 0.0 75+-5
16 40 700 4+-0.5 0.0 80+-10
16 40 800 5+-0.5 0.0 105+-10
16 40 900 6.+-0.5 0.0 135+-15


Back to Positrons

Retrieved from "https://wiki.iac.isu.edu/index.php?title=HRRL_radiation_tests&oldid=45492"