|
|
| Line 393: |
Line 393: |
| | | | |
| | :<math>I_{yy } = \int \rho \left (z^2+x^2 \right ) dV = \frac{3}{20} M R^2 + \frac{3Mh^2}{5}= \frac{3}{20} M \left ( R^2 + 4h^2 \right ) = I_{xx}</math> | | :<math>I_{yy } = \int \rho \left (z^2+x^2 \right ) dV = \frac{3}{20} M R^2 + \frac{3Mh^2}{5}= \frac{3}{20} M \left ( R^2 + 4h^2 \right ) = I_{xx}</math> |
| | + | |
| | + | The products of inertia are given by |
| | + | |
| | + | Products of Inertia of a rigid body rotating about the z-axis for the angular momentum along the x-axis |
| | + | |
| | + | :<math>I_{xz} \equiv \sum m_k(-x_{k} z_{k}) =\int \rho xy dV</math> |
| | + | |
| | + | From the viewpoint of the summation equation one can see that for every mass at point (x,z) there is an equal mass at the point (-x,z), |
| | + | Thus the sum will add to zero. |
| | + | |
| | + | Products of Inertia of a rigid body rotating about the z-axis for the angular momentum along the y-axis |
| | + | |
| | + | :<math>I_{yz} \equiv \sum m_k \left (-y_{k} z_{k} )\right ) </math> |
| | + | |
| | + | |
| | | | |
| | | | |
| − | :<math>I_{xy} =\int \rho xy dV</math>
| |
| | | | |
| | | | |
Rigid Body Motion
Rigid Body
- Rigidy Body
- A Rigid Body is a system involving a large number of point masses, called particles, whose distances between pairs of point particles remains constant even when the body is in motion or being acted upon by external force.
- Forces of Constraint
- The internal forces that maintain the constant distances between the different pairs of point masses.
Total Angular Momentum of a Rigid Body
Consider a rigid body that rotates about a fixed z-axis with the origin at point O.
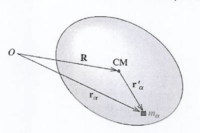
let
- [math]\vec R[/math] point to the center of mass of the object
- [math]\vec {r}_k[/math] points to a mass element [math]m_k[/math]
- [math]\vec{r}_k^{\;\;\prime}[/math] points from the center of mass to the mass element [math]m_k[/math]
the angular momentum of mass element [math]m_k[/math] about the point O is given as
- [math]\ell_k = \vec {r}_k \times \vec {p}_k = \vec {r}_k \times m \vec {\dot r}_k[/math]
The total angular momentum about the point O is given as
- [math] \vec L = \sum \ell_k = \sum \vec {r}_k \times m_k \vec {\dot r}_k[/math]
This can be cast in term of the angular momentum about the center of mass and the angular momentum of the CM motion
- [math]\vec {r}_k = \vec R + \vec{r}_k^{\;\; \prime}[/math]
- [math] \vec L = \sum \vec {r}_k \times m_k \vec {\dot r}_k[/math]
- [math] = \sum (\vec R + \vec{r}_k^{\;\; \prime}) \times m_k (\vec \dot R + \vec{\dot r}_k^{\;\; \prime})[/math]
- [math] = \sum \vec R \times m_k \vec \dot R + \sum \vec R \times m_k \vec{\dot r}_k^{\;\; \prime} + \sum \vec{r}_k^{\;\; \prime} \times m_k \vec \dot R +\sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\dot r}_k^{\;\; \prime} [/math]
- [math]\sum \vec R \times m_k \vec \dot R = \vec R \times \sum m_k \vec \dot R = \vec R \times M \vec \dot R = \vec R \times \vec P[/math]
- [math]\vec P =[/math] momentum of the center of Mass
- [math]\sum \vec R \times m_k \vec{\dot r}_k^{\;\; \prime} = \vec R \times \sum m_k \vec{\dot r}_k^{\;\; \prime} [/math]
- [math]\sum m_k \vec{\dot r}_k^{\;\; \prime} = \sum m_k \left ( \vec {r}_k - \vec R\right ) = \sum m_k \vec {r}_k - \sum m_k \vec R = \vec {v}_{cm} - \vec{v}_{cm} = 0[/math]
- The location of the center of mass is at [math]\vec{ r}_k^{\;\; \prime} = 0[/math] the derivative is also zero
- [math]\sum \vec{r}_k^{\;\; \prime} \times m_k \vec \dot R = \sum m_k \vec{r}_k^{\;\; \prime} \times \vec \dot R =0 [/math] : The location of the CM is at 0
- [math] \vec L = \vec R \times \vec P + \sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\dot r}_k^{\;\; \prime} [/math]
- [math] = L_{\mbox{CM}} + L_{\mbox{about CM}} [/math]
The total angular momentum is the sum of the angular momentum of the center of mass of a rigid body [math] L_{\mbox{CM}} [/math] and the angular momentum of the rigid body about the center of mass [math] L_{\mbox{about CM}} [/math]
Planet example
What is the total angular momentum of the earth orbiting the sun?
There are two components
- [math] \vec L_{\mbox{CM}} [/math] = angular momentum of the earth orbiting about the sun
- [math] \vec L_{\mbox{about CM}} [/math] = angular momentum of the earth orbiting about the earth's center of mass (Spin)
- [math]\vec L_{\mbox{tot}} = \vec L_{\mbox{CM}} + \vec L_{\mbox{about CM}}[/math]
- [math] \vec L_{\mbox{CM}} [/math] is conserved and defined as Orbital angular momentum
- [math]\vec \dot L_{\mbox{CM}} = \vec \dot R \times \vec P + \vec R \times \vec \dot P[/math]
- [math]\vec \dot R \times \vec P = \vec V \times M \vec V = 0[/math]
- [math]\Rightarrow \vec \dot L_{\mbox{orb}} = \vec R \times \vec \dot P=\vec R \times \vec {F}_{ext}[/math]
If there is only a central force
- [math]\vec {F}(\mbox{ext}) = G \frac{Mm}{R^3} \vec R[/math]
Then
- [math]\vec R \times \vec {F}(\mbox{ext}) = \vec R \times G \frac{Mm}{R^3} \vec R= G \frac{Mm}{R^3} \vec R \times \vec R =0
[/math]
Thus
- [math]\vec \dot L_{\mbox{CM}} = \vec R \times \vec {F}(\mbox{ext}) = 0[/math]
- [math]\vec L_{\mbox{CM}} \equiv \vec L_{\mbox{Orb}}[/math] = constant = Orbital angular momentum
The above is a good approximation even though the Sun's gravitational Field is not perfectly uniform
- How about [math]\vec L_{\mbox{about CM}}[/math]?
Since
- [math]\vec L_{\mbox{tot}} = \sum \vec {r}_k \times m_k \vec {\dot r}_k =\vec L_{\mbox{Orb}} + \vec L_{\mbox{about CM}}[/math]
as seen earlier
- [math] \vec L = \sum \vec {r}_k \times m_k \vec {\dot r}_k[/math]
- [math] = \sum (\vec R + \vec{r}_k^{\;\; \prime}) \times m_k (\vec \dot R + \vec{\dot r}_k^{\;\; \prime})[/math]
- [math] = \vec R \times \vec P + \sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\dot r}_k^{\;\; \prime} [/math]
Then
- [math]\dot \vec L = \vec \dot R \times \vec P +\vec R \times \vec \dot P + \sum \vec{\dot r}_k^{\;\; \prime} \times m_k \vec{\dot r}_k^{\;\; \prime} + \sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\ddot r}_k^{\;\; \prime} [/math]
- [math] =\vec R \times \vec \dot P + \sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\ddot r}_k^{\;\; \prime} [/math]
- [math] =\vec R \times \vec {F}(\mbox{ext}) + \sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\ddot r}_k^{\;\; \prime} [/math]
- [math] =\vec{\dot{ L}}_{\mbox{Orv}} + \vec{\dot {L}}_{\mbox{about CM}}[/math]
- [math]\Rightarrow \vec{\dot {L}}_{\mbox{about CM}} = \sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\ddot r}_k^{\;\; \prime} [/math]
- [math] \vec{\dot {L}}_{\mbox{spin}}\equiv\vec{\dot {L}}_{\mbox{about CM}} = \sum \vec{r}_k^{\;\; \prime} \times m_k \vec{\ddot r}_k^{\;\; \prime} \equiv \tau(\mbox{ext about CM}) [/math]
The total angular momentum is the sum of the orbital angular momentum and the spin
- [math]\vec L_{\mbox{tot}} = \vec L_{\mbox{orb}} + \vec L_{\mbox{spin}}[/math]
- Precession of the Earth
http://courses.physics.northwestern.edu/Phyx125/Precession%20of%20the%20Earth.pdf
Total Kinetic energy of a Rigid Body
Using the same coordinate system as above
the kinetic energy of mass element [math]m_k[/math] about the point O is given as
- [math]T_k = \frac{1}{2} m_k \left | \vec \dot{r}_k \right |^2[/math]
The total Kinetic about the point O is given as
- [math] \vec T = \sum \frac{1}{2} m_k \left | \vec \dot{r}_k \right |^2[/math]
Rewriting this again in terms of the location of the CM of the body [math]\vec R[/math] and the location of a mass element from the CM [math]\vec{r}_k^{\;\; \prime}[/math]
- [math]\vec {r}_k = \vec R + \vec{r}_k^{\;\; \prime}[/math]
- [math]\vec {\dot r}_k = \vec \dot R + \vec{\dot r}_k^{\;\; \prime}[/math]
- [math]\vec {\dot r}_k \cdot \vec {\dot r}_k = \left ( \vec \dot R + \vec{\dot r}_k^{\;\; \prime} \right ) \cdot \left ( \vec \dot R + \vec{\dot r}_k^{\;\; \prime} \right ) [/math]
- [math] = \left | \vec \dot R \right |^2 + \left | \vec{\dot r}_k^{\;\; \prime} \right |^2 + 2 \vec \dot R \cdot \vec{\dot r}_k^{\;\; \prime} [/math]
- [math] \vec T = \sum \frac{1}{2} m_k \left | \vec \dot{r}_k \right |^2[/math]
- [math] = \sum \frac{1}{2} m_k \left | \vec \dot R \right |^2 + \left | \vec{\dot r}_k^{\;\; \prime} \right |^2 + 2 \vec \dot R \cdot \vec{\dot r}_k^{\;\; \prime}[/math]
- [math] = \frac{1}{2} M \left | \vec \dot R \right |^2 + \frac{1}{2} \sum m_k \left | \vec{\dot r}_k^{\;\; \prime} \right |^2 + \vec \dot R \cdot \sum m_k \vec{\dot r}_k^{\;\; \prime}[/math]
For a Rigid body
- [math] \sum m_k \vec{\dot r}_k^{\;\; \prime} =0 [/math] The internal kinetic energy is zero for a rigid body, otherwise it would be expanding
- [math] \vec T = \frac{1}{2} M \left | \vec \dot R \right |^2 + \frac{1}{2} \sum m_k \left | \vec{\dot r}_k^{\;\; \prime} \right |^2 \cdot [/math]
- [math] = T_{\mbox{CM}} + T_{\mbox{about CM}}[/math]
Total Potential energy of a Rigid Body
If all forces are conservative
- [math]\vec \nabla \times \vec F_{ij} = 0[/math]
then a Potential Energy may be defined
- [math]\Delta U_{ij}(r_{ij}) \equiv -\int_{r_o}^r \vec{F}_{ij}(r_{ij}) \cdot d\vec{r}_{ij} = - W_{cons}[/math]
Then the potential energy of a rigid body is given by
- [math]\sum_{i\lt j} \Delta U_{ij}(r_{ij}) = U_{\mbox{int}} = [/math] constant
for a rigid body the inter-particle separation distance [math]r_{ij}[/math] is constant so the internal potential of a rigid body does not change
- Thus the kinematics of a Rigid body only needs to consider the potential energy of external forces.
Rotation about a fixed axis
Consider a Rigid body rotating with a speed [math]\vec \omega[/math] about a fixed axis (z-axis) with its origin at the point O
- [math]\vec \omega = \omega \hat k[/math]
The total angular momentum about the point O is given as
- [math] \vec L = \sum \ell_k = \sum \vec {r}_k \times m_k \vec {\dot r}_k[/math]
As seen in the non-inertial reference frame chapter
- [math]\vec \dot r = \vec v = \vec \omega \times \vec r[/math]
thus
- [math] \vec \omega \times \vec r_k = \left( \begin{array}{ccc} \hat i & \hat j & \hat k\\ 0 & 0 & \omega \\x_{k} & y_{k} & z_{k}\end{array} \right)= \omega \left ( - y_{k} \hat i + x_{k} \hat j \right ) [/math]
- [math] \vec {r}_k \times \vec {\dot r}_k = \vec {r}_k \times \vec \omega \times \vec r = \vec {r}_k \times \omega \left ( - y_{k} \hat i + x_{k} \hat j \right ) [/math]
- [math]= \left( \begin{array}{ccc} \hat i & \hat j & \hat k\\ x_{k} & y_{k} & z_{k} \\ -\omega y_{k} & \omega x_{k} & 0\end{array} \right)= \omega \left ( - z_{k}x_{k} \hat i - z_{k}y_{k} \hat j + \left (x_{k}^2+y_{k}^2 \right ) \hat k \right ) [/math]
- [math] \vec L = \sum \ell_k = \sum \vec {r}_k \times m_k \vec {\dot r}_k[/math]
- [math] = \omega \sum m_k \left ( - z_{k}x_{k} \hat i - z_{k}y_{k} \hat j + \left (x_{k}^2+y_{k}^2 \right ) \hat k \right )[/math]
Moments (Products) of Inertia about the fixed axis
- [math]L_z = \omega \sum m_k \left (x_{k}^2+y_{k}^2 \right )[/math]
Let
- [math]I_{zz} \equiv \sum m_k \left (x_{k}^2+y_{k}^2 \right ) =[/math] moment of inertia about the z-axis in the "z" ([math]\hat k[/math]) direction.
Then
- [math]L_z = I_{zz} \omega[/math]
Similarly
Products of Inertia of a rigid body rotating about the z-axis for the angular momentum along the x-axis
- [math]I_{xz} \equiv \sum m_k(-x_{k} z_{k}) [/math]
Products of Inertia of a rigid body rotating about the z-axis for the angular momentum along the y-axis
- [math]I_{yz} \equiv \sum m_k \left (-y_{k} z_{k} )\right ) [/math]
- [math] \vec L =\omega \left ( I{xz} \hat i + I{yz} \hat k + I{zz} \hat k \right )[/math] = angular momentum about the z-axis
- Example
- Moment of Inertia of a sphere
Find the moment of inertia of a uniform solid sphere of Radius (R) and mass (M) about its diameter.
Using a coordinate system with its origin at the center of the sphere
For a set of discrete masses
- [math]I_{zz} \equiv \sum m_k \left (x_{k}^2+y_{k}^2 \right ) =[/math] moment of inertia about the z-axis in the "z" ([math]\hat k[/math]) direction.
For a mass distribution the above summation is written in integral form as
- [math]I_{zz} = \int dm_k \left (x_{k}^2+y_{k}^2 \right ) [/math]
one may define the sphere's density as
- [math]\rho = \frac{M}{\frac{4}{3} \pi R^3}[/math]
A differential mass is written as
- [math]dm_k = \rho dV_k = [/math] Imagine a differential circle in the x-y plane that you integrate along z
if using spherical coordinates
- [math]x_k = r \sin \theta \cos \phi \;\;\;\; y_k = r \sin \theta \sin \phi[/math]
- [math]x_k^2 + y_k^2 = r^2 \sin^2 \theta[/math]
- [math]I_{zz} = \int dm_k \left (x_{k}^2+y_{k}^2 \right ) [/math]
- [math]= \rho \int r^2 dV_k = \rho \int (r \sin \theta )^2 dV_k = \rho \int r^2 \sin^2 \theta (r^2 dr \sin \theta d \theta d \phi)[/math]
- [math]= \rho \int_0^R r^4 dr \int_0^{\pi} \sin^3 \theta d \theta \int_0^{2\pi} d \phi[/math]
- [math]= \frac{8 \pi}{15} \rho R^5 = \frac{2}{5} MR^2[/math]
- [math]dV = r^2 dr \sin \theta d \theta d \phi[/math]
- The moment of Inertia of a hollow sphere of outer radius [math]b[/math] and inner radius [math]a[/math]
Moments of Inertia, like masses, add and subtract like scalers.
- [math]I(b,a) = I(b,0) - I(a,o) = \frac{8 \pi}{15} \rho (b^5 - a^5)[/math] = Moment of inertia of a sphere of inner radius [math]a[/math] and outer radius [math]b[/math].
- [math]\rho = \frac{M}{V} = \frac{M}{\frac{4 \pi}{3} (b^3 - a^3)}[/math]
- [math]I(b,a) = \frac{2}{5} M \frac{ (b^5 - a^5)}{ (b^3 - a^3)}[/math] = Moment of inertia of a sphere of inner radius [math]a[/math] and outer radius [math]b[/math].
Moment of inertia tensor
The angular momentum for a body spinning about an arbitrary axis.
let
- [math]\vec \omega = \omega_x \hat i + \omega_y \hat j + \omega_z \hat k[/math]
Consider a Rigid body rotating with a speed [math]\vec \omega[/math] about a fixed axis (z-axis) with its origin at the point O
- [math]\vec \omega = \omega \hat k[/math]
The total angular momentum about the point O is given as
- [math] \vec L = \sum \ell_k = \sum \vec {r}_k \times m_k \vec {\dot r}_k= \sum m_k \left [ \vec {r}_k \times \vec {\dot r}_k \right ][/math]
As seen in the non-inertial reference frame chapter
- [math]\vec \dot r = \vec v = \vec \omega \times \vec r[/math]
thus
- [math] \vec \omega \times \vec r_k = \left( \begin{array}{ccc} \hat i & \hat j & \hat k\\ \omega_x & \omega_y & \omega_z \\x_{k} & y_{k} & z_{k}\end{array} \right)= \left ( \omega_y z_{k} - \omega_z y_k \right ) \hat i + \left ( \omega_z x_{k} - \omega_x z_k \right ) \hat j + \left ( \omega_x y_{k} - \omega_y x_k \right ) \hat k [/math]
- [math] \vec {r}_k \times \vec {\dot r}_k = \vec {r}_k \times \vec \omega \times \vec r = \vec {r}_k \times \omega \left ( - y_{k} \hat i + x_{k} \hat j \right ) [/math]
- [math]= \left( \begin{array}{ccc} \hat i & \hat j & \hat k\\ x_{k} & y_{k} & z_{k} \\ \left ( \omega_y z_{k} - \omega_z y_k \right ) & \left ( \omega_z x_{k} - \omega_x z_k \right ) & \left ( \omega_x y_{k} - \omega_y x_k \right ) \end{array} \right) [/math]
- [math]L_x = \sum m_k \left [ \left . \vec {r}_k \times m \vec {\dot r}_k \right |_x \right ][/math]
- [math]=\sum m_k \left [ y_k \left ( \omega_x y_{k} - \omega_y x_k \right )-z_k \left ( \omega_z x_{k} - \omega_x z_k \right ) \right ] [/math]
- [math]= \sum m_k \left [ \left ( y_{k}^2 + z_k ^2 \right )\omega_x - y_k x_k \omega_y - z_k x_{k} \omega_z \right ][/math]
- [math]L_y = \sum m_k \left [ \left . \vec {r}_k \times m \vec {\dot r}_k \right |_y \right ][/math]
- [math]= \sum m_k \left [ z_k \left ( \omega_y z_{k} - \omega_z y_k \right ) -x_k \left ( \omega_x y_{k} - \omega_y x_k \right ) \right ][/math]
- [math]= \sum m_k \left [ -x_ky_k \omega_x + \left ( z_{k}^2 +x_k^2\right ) \omega_y - z_k y_k \omega_z \right ][/math]
- [math]L_z = \sum m_k \left [ \left . \vec {r}_k \times m \vec {\dot r}_k \right |_z \right ][/math]
- [math] =\sum m_k \left [ x_k \left ( \omega_z x_{k} - \omega_x z_k \right ) - y_k \left ( \omega_y z_{k} - \omega_z y_k \right) \right ][/math]
- [math] =\sum m_k \left [ -x_k z_k \omega_x - y_k z_k \omega_y +\left ( x_{k}^2 + y_k^2 \right)\omega_z \right ][/math]
- The Moment of Inertia tensor is defined such that
- [math]\tilde{I} = \left( \begin{array}{ccc} \sum m_k\left ( y_{k}^2 + z_k ^2 \right ) & - \sum m_k y_k x_k & - \sum m_kz_k x_{k}\\ -\sum m_kx_ky_k & \sum m_k\left ( z_{k}^2 +x_k^2\right ) & - \sum m_kz_k y_k \\ -\sum m_kx_k z_k & - \sum m_ky_k z_k & \sum m_k\left ( x_{k}^2 + y_k^2 \right) \end{array} \right) [/math]
- [math] \vec L = \tilde{I} \vec \omega \;\;\;\;\;\; \mbox {or} \;\;\;\;\;\; L_i = \sum_{j=1}^3 I_{ij} \omega_j [/math]
- The diagonals of the moment of inertia tensor are the usual moments of inertia
- The off-diagonals are the six products of inertia
- [math]I_{ij} = - \sum_{\alpha} m_{\alpha} i_{\alpha} j_{\alpha}[/math] where [math]i[/math] & [math]j[/math] represent [math]x,y,z[/math] components and [math]i\ne j[/math]
- [math]I_{ii} = \sum_{\alpha} m_{\alpha} j_{\alpha} k_{\alpha}[/math] where [math]j[/math] & [math] k[/math] represent [math]x,y,z[/math] components and [math]i\ne j \ne k [/math]
- Note
- [math] \tilde I = \tilde I^{\;\;T}[/math] The inertia tensor is symmetric ( i.e. it is it's own transpose) or in other words
- [math]I_{ij} = I_{ji}[/math]
Inertia Tensor for a solid cone
Find the moment of inertia tensor for a uniform solid cone of mass [math]M[/math] , height [math]h[/math] , and base radius [math]R[/math] spinning about its tip.
Choose the z-axis so it is along the symmetry axis of the cone.
The mass density may be written as
- [math]\rho = \frac{M}{V}[/math]
Using cylindrical coordinates ( [math]r, \phi, z[/math]) the volume of a cone is given by
- [math]V = \int_0^h dz \int _o^{2\pi}d\phi \int_0^{\frac{Rz}{h}} r dr = \int_0^h dz \int _o^{2\pi}d\phi \frac{R^2z^2}{2h^2}= 2 \pi \frac{R^2}{2h^2}\int_0^h z^2 dz [/math]
- [math] = \pi \frac{R^2}{h^2} \frac{h^3}{3} =\frac{1}{3} \pi R^2 h [/math]
the radius of the base of the cone may be written as a function such that [math] r=\frac{Rz}{h}[/math] .
When [math]z=0 \Rightarrow r=0[/math] and when [math]z=h \Rightarrow r = R[/math]
- [math]\rho = \frac{M}{V} = \frac{M}{\frac{1}{3} \pi R^2 h} = \frac{ 3 M}{\pi R^2 h} [/math]
calculating the moment of inertia about the z-axis :
- [math]I_{zz} = \int \rho \left (x^2+y^2 \right ) dV= \int_0^h \int _o^{2\pi} \int_0^{\frac{Rz}{h}} \rho r^2 r dr d\phi dz[/math]
- [math]I_{zz} = \rho \int_0^h dz \int _o^{2\pi}d\phi \int_0^{\frac{Rz}{h}} r^2 r dr [/math]
- [math] = \rho \int_0^h dz (2 \pi) \frac{R^4z^4}{4h^4} [/math]
- [math] = 2 \pi \rho \frac{R^4}{4h^4}\int_0^h z^4 dz [/math]
- [math] = 2 \pi \rho \frac{R^4}{4h^4} \frac{h^5}{5} [/math]
- [math] = 2 \pi \left ( \frac{ 3 M}{\pi R^2 h}\right ) \frac{R^4}{4h^4} \frac{h^5}{5} [/math]
- [math] = 3 M \frac{R^2}{2h^5} \frac{h^5}{5} = \frac{3}{10} M R^2 [/math]
- [math]I_{xx} = \int \rho \left (z^2+y^2 \right ) dV= \int \rho z^2 dV +\int \rho y^2 dV[/math]
Since
- [math]I_{zz} = \int \rho \left (x^2+y^2 \right ) dV[/math]
and the cone is symmetric in the x-y plane
- [math]\int \rho y^2 dV = \frac{1}{2} I+{zz}[/math]
- [math] \int \rho z^2 dV = \rho \int_0^h z^2 dz \int _o^{2\pi}d\phi \int_0^{\frac{Rz}{h}} r dr = 2 \pi \rho \int_0^h z^2 dz \frac{R^2z^2}{2h^2} [/math]
- [math] = \pi \rho \frac{R^2}{h^2}\int_0^h z^4 dz = \pi \rho \frac{R^2}{h^2} \frac{h^5}{5} [/math]
- [math] = \pi \left ( \frac{ 3 M}{\pi R^2 h}\right ) frac{R^2h^3}{5} = \frac{3Mh^2}{5} [/math]
- [math]I_{xx} =\frac{3}{20} M R^2 + \frac{3Mh^2}{5}[/math]
- [math]I_{yy } = \int \rho \left (z^2+x^2 \right ) dV = \frac{3}{20} M R^2 + \frac{3Mh^2}{5}= \frac{3}{20} M \left ( R^2 + 4h^2 \right ) = I_{xx}[/math]
The products of inertia are given by
Products of Inertia of a rigid body rotating about the z-axis for the angular momentum along the x-axis
- [math]I_{xz} \equiv \sum m_k(-x_{k} z_{k}) =\int \rho xy dV[/math]
From the viewpoint of the summation equation one can see that for every mass at point (x,z) there is an equal mass at the point (-x,z),
Thus the sum will add to zero.
Products of Inertia of a rigid body rotating about the z-axis for the angular momentum along the y-axis
- [math]I_{yz} \equiv \sum m_k \left (-y_{k} z_{k} )\right ) [/math]
http://scienceworld.wolfram.com/physics/MomentofInertiaSphere.html
http://www.phys.ufl.edu/~mueller/PHY2048/2048_Chapter10_F08_Part2_lecture.pdf
Principle Axis
as seen before, the angular momentum of a rigid body rotating about a fixed axis ( the z-axis in this case) is given by
- [math] \vec L = \sum \ell_k = \sum \vec {r}_k \times m_k \vec {\dot r}_k[/math]
- [math] = \omega \sum m_k \left ( - z_{k}x_{k} \hat i - z_{k}y_{k} \hat j + \left (x_{k}^2+y_{k}^2 \right ) \hat k \right )[/math]
Although the object was only rotating about the z-axis, there are angular momentum components along the other directions
In other words, unlike what you learned in introductory physics
- [math]\vec L \ne I \vec \omega[/math] in general
instead the general expression for angular momentum is
- [math]\vec L = \vec r \times \vec p[/math] is the more general statement
Consider the Kinetic energy of a rotating rigid body in terms of the sum of the kinetic energy of all of its fixed mass elements
- [math]T = \frac{1}{2} \sum_k m_k v_k^2[/math]
If the body is only rotating about the z-axis then
- [math]v_k = r_k \omega[/math]
- [math]\Rightarrow T = \frac{1}{2} \sum_k m_k r_k^2 \omega = \frac{ \omega}{2} \sum_k m_k r_k^2[/math]
- [math]= \omega I_z \equiv L_z[/math]
example of the tensor
Forest_Ugrad_ClassicalMechanics#Rigid_Body_Motion
