Forest UCM Ch3 Rockets

Rocket problem 1

Remember the hobo problem? This is how rockets are propelled by expending fuel (mass).

Lets first think about the inverse rocket where mass is added instead of expelled.

Consider a railroad car with frictionless wheels moving at speed $v$ on level ground.

A hobo handing from a tree drops down onto the railroad car as it is moving under the tree.

What is the final velocity of a railroad car after the hobo jumps on.

Conservation of momentum

$Mv = (M+m) v_f$

$v_f = \frac{M}{M+m} v$

The railroad car slows down after the hobo jumps on.

Rockets work in a similar fashion. They speed up after the fuel "jumps" off.

Rocket Problem 2

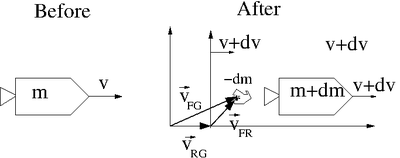
Consider a rocket of mass $m$ moving at a speed $v$ ejecting rocket fuel for propulsion.

File:Forest UCM Ch3 Rockets Fig.xfig.txt

$m =$ mass of Fuel + Rocket

$-dm =$ mass of Fuel ejected over time interval $dt$ ( $dm$ = mass lost by rocket < 0)

$u =v_{FR}$ velocity of Fuel relative to the Rocket

$v =$ velocity of rocket relative to the ground before ejecting fuel of mass $(-dm)$

$v+dv =v_{RG}$ velocity of the rocket relative to the ground after ejecting fuel

$V_FG =$ Velocity of the fuel with respect to the ground

Apply Conservation of Momentum

$mv = (-dm)V_{FG} + (m-(-dm))(v+dv)$

$dmV_{FG} = mdv + dm (v+dv)$

The velocity of the fuel with respect to the ground$(V_{FG})$ may be written as the vector sum of the rocket's velocity with respect to the ground $(V_{RG})$ and the velocity of the fuel with respect to the rocket $(V_{FR})$ :Galilean transormation

$\vec{V}_{FG} - \vec{V}_{FR} + \vec{V}_{RG}$

assuming 1-D motion and using the velocity variables defined above

$V_{FG} = -u + (v+dv)$

substituting

$dm \left (-u + (v+dv) \right ) = mdv + dm (v+dv)$

$-udm = mdv$

solving for the velocity

$\int_{v_0}^v = \int_{m_0}^m -u \frac{dm}{m}$

$v - v_0 = u \ln \left (\frac{m_0}{m} \right )$

$v = v_0 + u \ln \left (\frac{m_0}{m} \right )$

where $m_0$ is the initial Rocket mass

In terms of Thrust

Defining

$\mbox{THRUST} = - \dot{m} u$

Then

$m \dot{v} =$ THRUST = Force on rocket as a result of expelling fuel

Forest_UCM_MnAM#Rockets