Forest Relativity Notes

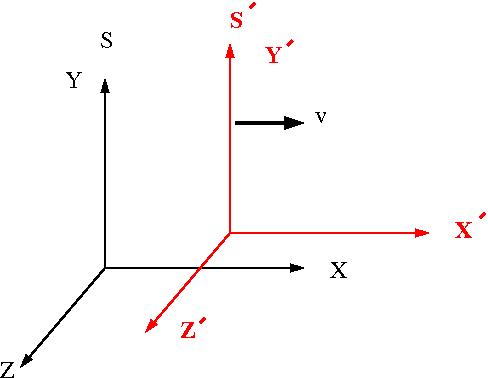
Lorentz Transformations

The picture below represents the relative orientation of two different coordinate systems [math](S, S^{\prime})[/math] . [math]S[/math] is at rest (Lab Frame) and [math]S^{\prime}[/math] is moving at a velocity v to the right with respect to frame [math]S[/math].

The relationship between the coordinate[math] (x,y,z,ct)[/math] of an object in frame [math]S[/math] to the same object described using the coordinates [math](x^{\prime},y^{\prime},z^{\prime},ct^{\prime})[/math] in frame [math]S^{\prime}[/math] is geven by the Lorentz transformation:

4- vector notation

The 4-vector notation is given as

[math]x^{\mu^{\prime}} = \sum_{\nu=0}^3 \Lambda_{\nu}^{\mu} x^{\nu}[/math]

where

[math] x^0 \equiv ct[/math]

[math]x^1 \equiv x[/math]

[math]x^2\equiv y[/math]

[math]x^3\equiv z[/math]

[math]\Lambda = \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ][/math]

[math]\beta = \frac{v}{c} = \frac{pc}{E}[/math]

[math]\gamma = \frac{1}{\sqrt{1 -\beta^2}} = \frac{E_{tot}}{mc^2}[/math]

NOTE

It is common in particle physics to define [math] c \equiv 1[/math] making [math]\gamma = \frac{E}{m}[/math] where [math]m[/math] is in units of [math]\frac{\mbox{MeV}}{\mbox{c}^2}[/math]

example

[math]x^{0^{\prime}} = \sum_{\nu=0}^2 \Lambda_{\nu}^0 x^{\nu} = \Lambda_0^0 x^0 + \Lambda_1^0 x^1 \Lambda_2^0 x^2 + \Lambda_3^0 x^2[/math]

[math]ct^{\prime}= \gamma x^0 - \gamma \beta x^1 + 0 x^2 + 0 x^3 = \gamma ct - \gamma \beta x = \gamma(ct -\beta x)[/math]

Or in matrix form the tranformation looks like

[math]\left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix} \right )[/math]

Note

Einstein's summation convention drops the [math]\sum[/math] symbols and assumes it to exist whenever there is a repeated subscript and uperscript

ie; [math]x^{\mu^{\prime}} = \Lambda_{\nu}^{\mu} x^{\nu}[/math]

in the example above the[math] \nu[/math] symbol is repeated thereby indicating a summation over [math]\nu[/math].

Momentum 4-vector

[math]p^{\mu} \equiv (\frac{E}{c} , \vec{p})[/math]

[math]p_{\mu} \equiv (\frac{E}{c} , -\vec{p})[/math]

[math]p_{\mu}p^{\mu} = \frac{E^2}{c^2} - p^2 \equiv E^2 - p^2 = m^2[/math]

Note

There is another convention used for 4-vector notation by Perkins and Koller which goes like this

[math]p^{\mu} \equiv (\vec{p},iE)[/math]

[math]p_{\mu} \equiv (\vec{p},iE)[/math]

Trig Method

Another way to represent the lorentz transformation is by using the substitution

[math]\sin (\alpha) \equiv \beta \equiv \frac{v}{c}[/math]

[math]\cos(\alpha) \equiv \frac{1}{\gamma} \equiv \sqrt{1 - \beta^2}[/math]

The Matrix form pf the tranformation looks like

[math]\left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \sec(\alpha) & -\tan(\alpha) & 0 & 0 \\ -\tan(\alpha) & \sec(\alpha) &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix} \right )[/math]

Or the reverse transformation

[math]\left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix}\right )= \left [ \begin{matrix} \sec(\alpha) & \tan(\alpha) & 0 & 0 \\ \tan(\alpha) & \sec(\alpha) &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )[/math]

Notice that you just needed to change the signs for the inverse matrix [math]\Lambda^{-1}[/math]

Proper Time and Length

Proper Time

Proper Time [math]\Tau[/math]

The time measured in the rest frame of the clock. The time interval is measured at the same x,y,z coordinates because the clock chose is in a frame which is not moving (rest frame).

The time given in any frame (t) = [math]\gamma \Tau[/math]

Note

since [math]\gamma \gt 1[/math] you expect the Proper time interval to be the smallest

Proper Length

Proper Length[math] (c\Tau)[/math]

The length of an object in the object's rest frame.

Transformation Examples

Decay of Particle to 2 Bodies

Consider the decay of the [math]\rho_0[/math] meson at rest into two pions ([math]\pi^+[/math] and [math]\pi^-[/math] )

File:NeutralRhoMesonDecayDiagram.jpg

The diagram above shows a [math]\rho_0[/math] meson at rest in the lab which then decays into two pions of momentum [math]p_1[/math] and [math]p_2[/math] in the center of momentum frame of the [math]\rho_0[/math] meson.

If [math]P^{\mu}[/math] represent the total momentum of the system before the decay then

[math]P^{\mu} = (E,0) =(M,0) = \left ( p_1 \right )^{\mu} + \left ( p_2 \right)^{\mu}[/math]

[math]\Rightarrow 0 = \vec{p}_1 + \vec{p}_2[/math]

or

[math]\vec{p}_1 = - \vec{p}_2[/math]

Let

[math]p \equiv |\vec{p}_1 | = |\vec{p}_2 |[/math]

Conservation of Energy

[math]\Rightarrow E_{tot} = M = E_1 + E_2 = \sqrt{m_1^2 + p^2} + \sqrt{m_2^2 + p^2}[/math]

solving for p

[math]\Rightarrow p = \frac{1}{2M} \sqrt{[M^2 - (m_1-m_2)^2][M^2-(m_1+m_2)^2]}[/math]

[math]\Rightarrow M \ge m_1 + m_2[/math] is required to avoid the unphysical condition that the momentum of the particles after a decay would be an imaginary number

Using

[math]p \equiv |\vec{p}_1 | = |\vec{p}_2 |[/math]

[math]E_1^2 - m_1^2 = E_2^2 - m_2^2[/math]

[math]\Rightarrow E_2 = \sqrt{E_1^2 - m_1^2 + m_2^2}[/math]

Combine this with the conservation of energy equation above:

[math] E_1 + E_2 = E_1 + \sqrt{E_1^2 - m_1^2 + m_2^2} = M[/math]

[math]\Rightarrow E_1 - M = \sqrt{E_1^2 - m_1^2 + m_2^2}[/math]

Square both sides of the above equation

[math]E_1^2 -2ME_1 + M^2 = E_1^2- m_1^2 + m_2^2[/math]

[math]\Rightarrow E_1 = \frac{M^2+m_1^2-m_2^2}{2M}[/math]

Similarly

[math] E_2 = \frac{M^2+m_2^2-m^2_1}{2M}[/math]

Note

[math]\vec{p}_1 = -\vec{p}_2[/math]

[math]\Rightarrow[/math] The daughter particles (pions) from the decay of the Mother particle [math](\rho)[/math] travel in opposite directions with respect to eachother ( ie; they are "back - to -back")

This means that there is no preferential direction for the decay (the particles are distributed isotropically such that they are back-to-back)

Decay of Moving Particle to 2 Bodies (decay in flight)

[math]P^{\mu} = (E,\vec{p}_{tot}) =(M,\vec{p}_{tot}) = \left ( p_1 \right )^{\mu} + \left ( p_2 \right)^{\mu}[/math]

Assuming that the Mother particle is moving along the Z-axis, then the momentum of the daughter particles which perpendicular to the Z-axis (transverse components:[math]\vec{p}_{1,\perp}[/math] and [math]\vec{p}_{2,\perp}[/math]) are equal and opposite by conservation of momentum.

[math]\vec{p}_{\perp}\equiv -\vec{p}_{2,\perp}[/math]

The center of momentum frame is moving such that

[math]\beta_{CM} = \frac{p_{tot}}{M}[/math]

[math]\gamma_{CM} = \frac{E_{tot}}{M}[/math]

A Lorentz transformation of the kinematics for particle 1 between the Center of Momentum (cm) frame and the lab is given by:

[math]E_1 = \gamma_{cm}(E_1^{CM} + \beta_{cm}p_{1,z}^{CM})[/math]

[math]p_{1,z} = \gamma_{CM}(p_{1,z}^{CM} + \beta_{cm} E_1^{CM})[/math]

[math]p_{\perp} = p_{\perp}^{CM}[/math]

where

[math]E_1^{CM}[/math] = Kinetic Energy (not total) of particle 1 in the center of momentum (CM) reference frame

[math]p_{1,z}^{CM}[/math] = momentum of particle 1 along the direction of the mother particle in the CM frame

[math]p_{1,\perp}[/math] = the component of particle 1's momentum perpendicular to Mother particle's momentum

You can now use the results for [math]E_1[/math] and [math]p_1=p[/math] from the previous section where the Mother particle is at rest to determine the kinematics of the particles in the lab frame given that you know the initial 4-Momentum of the mother particle. You will need to specify the daugher decay angles in the CM frame in order to find the momentum components [math]p_z[/math] and [math]p_{\perp}[/math].

It can be shown that the lab angle for daughter particle 1 ([math]\theta_1[/math]) is given by

[math]\tan(\theta_1) = \frac{\sin(\theta_1^{CM})}{\gamma_{CM}\left (\frac{\beta_{CM}}{\beta_1^{CM}} + \cos(\theta_1^{CM}) \right )}[/math]

where

[math]\beta_1{CM} = \frac{p_1}{E} = \beta[/math] for daughter particle 1 in CM frame.

One could also find [math]\vec{p}_1[/math] without using the Lorentz transformation. Just use conservation of Energy and Momentum:

[math]E_{tot} = E_1^{tot} + E_2^{tot} = \sqrt{m_1^2 + p_1^2} + \sqrt{m_1^2 + p_1^2}[/math]

[math]\vec{p_{tot}} = \vec{p}_1 + \vec{p}_2[/math]

Solve the conservation of momentum equation for [math]p_2^2[/math]

[math]p_2^2 = (\vec{p_{tot}}- \vec{p}_1)^2 [/math]

and substitute the above for [math]p_2^2[/math] in the Conservation of Energy equation above. The dot product gives you the angle between the daughter momentum and thee Mother momentum ([math]\theta_1[/math]) as a variable. After a lot of algebra you can show that

[math]p_1 = \frac{\left ( M^2 + m_1^2 -m_2^2 \right ) p_{tot} \cos(\theta_1) \pm 2E\sqrt{M^2p^2 - m_1^2p^2_{tot} \sin^2(\theta_1)}}{2 \left( M^2 + p^2 \sin^2(\theta_1)\right )}[/math]

Note

[math]p[/math] is the momentum of the two daughter particles in the CM frame which was derived when the Mother particle wa at rest. [math]p_{tot}[/math] is the momentum of the Mother particle.

In order for a real solution

[math]M^2p^2 - m_1^2p^2_{tot} \sin^2(\theta_1) \gt 0[/math]

[math]\Rightarrow \frac{M p}{m_1 p_{tot}} \gt \sin(\theta_1)[/math]

If [math]\frac{M p}{m_1 p_{tot}} \gt 1[/math] then [math]\theta_1[/math] can be any angle and the "-" sign possibility in "[math]\pm[/math]" is rejected to avoided negative values for [math]p_1[/math] when \[math]theta_1[/math] > [math]\frac{\pi}{2}[/math].

If [math]\frac{M p}{m_1 p_{tot}} \lt 1[/math] then the maximum emmission angle for daughter 1 is given by

[math]\sin(\theta_1)|_{max} = \frac{M p}{m_1 p_{tot}}[/math]

The "[math]\pm[/math]" is kept because for each [math]\theta_1 \lt \theta_1 |_{max}[/math] there are two possible trajectories for daughter particle 1 and as a result 2 trajectories for daughter particle 2.

Decay of Particle to 3 Bodies (Dalitz plot)

Now lets consider the case where a Mother particle of mass [math]M[/math] decays into 3 daughter particles of masses [math]m_1[/math], [math]m_2[/math], and [math]m_3[/math]. The 4-mometum conservation is written as

[math]P^{\mu} = \left ( p_1 \right )^{\mu} +\left ( p_2 \right )^{\mu} +\left ( p_3 \right )^{\mu}[/math]

The following invariants are defined

[math]s = P_{\mu}P^{\mu} = M^2[/math]

[math]s_1 = \left (P -p_1 \right)_{\mu}\left (P -p_1 \right)^{\mu}=\left (p_2 + p_3 \right)_{\mu}\left (p_2 + p_3 \right)^{\mu}[/math]

[math]s_2 = \left (P -p_2 \right)_{\mu}\left (P -p_2 \right)^{\mu}=\left (p_3 + p_1 \right)_{\mu}\left (p_3 + p_1 \right)^{\mu}[/math]

[math]s_3 = \left (P -p_3 \right)_{\mu}\left (P -p_3 \right)^{\mu}=\left (p_1 + p_2 \right)_{\mu}\left (p_1 + p_2 \right)^{\mu}[/math]

The invariants [math]s_1[/math], [math]s_2[/math] and [math]s_3[/math] are not independent (the motivation for what is known as a Dalitz plot). Based on the definitions of these invariants and 4-momentum conversation one can show that

[math]s_1 + s_2 + s_3 = M^2 + m_1^2 + m_2^2 +m_3^2 [/math]

Also Note

[math]\sqrt{s_1}[/math] is the invariant mass of a subsystem defined by treating daughter particles 2 and 3 as one object. similar interpretations for [math]\sqrt{s_2}[/math] and [math]\sqrt{s_3}[/math].

Phase space

Phase space

In this type of problem, Phase space represents a kinematics range (space) spanned by any set of INDEPENDENT kinematic variables.

Elastic Scattering

Given the elastic scattering of 2 particles such that the following properties are

Known

[math]m_1[/math] = mass of the incident particle #1

[math]m_2[/math] = mass of the target particle (at rest) #2

[math]p_1[/math] = momentum of the incident particle #1

[math]\theta_1[/math] = scattering angle of particle #1

You can show that

[math]p_1^{\prime} = \frac{-B \pm \sqrt{B^2 -4AC}{2A}[/math] = Final momentum of scattered particle #1

[math]p_2^{\prime} = \left ( p_1^{\prime} \right )^2 -2p_2p_1^{\prime}\cos(\theta_1) + p_1^2[/math] = Final momentum of the target particle

[math]\sin (\theta_2) = - \frac{p_1^{\prime} \sin(\theta_1)}{p_2^{\prime}}[/math]

where

[math]A = \left ( \sqrt{p_1^2 +m_1^2} +m_2 \right )^2 -p_1^2 \cos^2(\theta_1)[/math]

[math]B = -2p_1 \cos(\theta_1) \left ( m_1^2 + m_2 \sqrt{p_1^2 + m_1^2}\right )[/math]

[math]C = - \left [ m_1^4 + (m_2^2 -m_1^2)(p_1^2 + m_1^2) -m_1^2m_2^2\right ][/math]