Forest ModernPhysics

Matter Waves (Wave Particle Duality)

Special relativity said that

[math]E = pc[/math] if m=0

Plank said he could fit the Black Body radiation data assuming that that

[math]E= hf[/math] where [math]h = 6.63 \times 10^{-34} \mbox{ J} \cdot \mbox{s}[/math] = Plank's constant

Combining the two we have

[math] p=\frac{E}{c} = \frac{ h f}{c}[/math]

[math]\Rightarrow[/math] photons have momentum like a particle (mv)

Do particles reciprocate and behave like photons?

De Broglie's Hypothesis

If photons can behave like particles by having momentum

Then can a particle behave like a wave by having wavelength

[math] p=\frac{ h f}{c} = \frac{h}{\lambda}[/math]

or

[math]\lambda_{particle} = \frac{h}{p}=[/math] de Broglie Hypothesis

Davisson and Germer

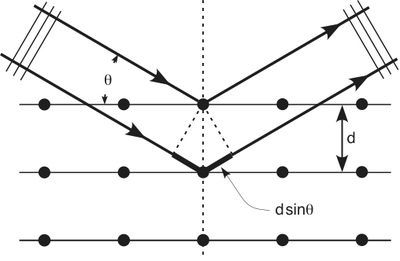
We know that X-rays having a wavelength of [math]\lambda_{X-rays} = 7.1 \times 10^{-11} \mbox{m}[/math] make a diffraction pattern on an aluminum foil. The waves diffract around the obstacle and then constructively interfere according to

[math]2 d sin \theta = n \lambda[/math]

where [math]d[/math] is the spacing between crystal planes, [math]\theta[/math] is the reflected angle, and [math]\lambda[/math] is the X-ray wavelength. The order of the diffraction maxima is given by [math]n[/math]. The picture below should have a max in the center but the intensity is so high that it has been blocked in order to avoid washing out the picture.

[math]p_{X-ray} = \frac{h}{\lambda} = \frac{6.63 \times 10^{-34} \mbox{ J} \cdot \mbox{s}}{7.1 \times 10^{-11}\mbox{m}} \frac{1 \mbox{eV}}{1.6 \times 10^{-19} \mbox{J}}[/math]

[math]= 5.8 \times 10^{-4} \frac{3 \times 10^{8}\mbox{m/s}}{c}[/math]

[math]= 1.75 \times 10^{4} \frac{\mbox{eV}}{c}[/math]

[math]= 17.5 \frac{\mbox{keV}}{c}\Rightarrow \mbox{E}=17.5 \mbox{keV}[/math]

Another way to calculate

[math]p_{X-ray} = \frac{hc}{\lambda c} = \frac{1240\mbox{ eV} \cdot \mbox{nm}}{0.071 \mbox{nm}\cdot \mbox{c}}= 17.5 \frac{\mbox{keV}}{c}[/math]

What would be the energy of an electron with the same wavelength as the above X-ray?

relativistic total energy relation

[math]E_{tot} = \sqrt{(pc)^2 + (mc^2)^2}[/math]

[math]= \sqrt{(17.5 keV)^2 + (511 keV)^2}[/math]

= 511.3 keV

relativistic kinetic energy

[math]K = E - mc^2 = (\gamma-1)mc^2 = 0.3 \mbox{keV} = 300 \mbox{eV}[/math]

Note [math]\beta = \frac{pc}{E_{tot}} = \frac{17.5 \mbox{keV}}{511 \mbox{keV}} = 0.03 \Rightarrow[/math] classical physics may be used for electrons below 50 keV

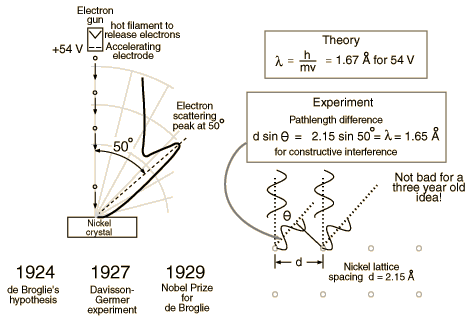
Clinton Davisson and Lester Germer in 1927 published conclusive evidence for the diffraction of electron waves using 54 eV electrons impinging a crystal made of nickel.

One problem to overcome for the experiment was that such a low energy electron scatters in air. The had to do the experiment in a vacuum.

From hyperphysics:

Bragg Diffraction

Quantization of Atomic Energy Levels

Absorption

Shine white light on a gas then send the transmitted light through a prism you will see some wavelengths are mission.

Emission

Heat up a gas and light of specific wavelengths will be emitted.

Balmer-Rydberg Formula

Balmer found that the specific wavelengths oberved using Hydrogen obeyed the relation

[math]\frac{1}{\lambda} = R \left ( \frac{1}{4} - \frac{1}{n^2}\right )[/math]

where

[math]R = 0.0110 \mbox{nm}^{-1}[/math]

Rydberg generalized the eqation to

[math]\frac{1}{\lambda} = R \left ( \frac{1}{n^{\prime^2}} - \frac{1}{n^2}\right )[/math]

where [math]n \gt n^\prime[/math] and both are integers

Bohr Model of the Atom

[1] Forest_Classes