Fermi's Golden Rule
Fermi's Golden rule is used to calculate the probability (per unit time) of a quantum mechanical transition between two particles ( a and b) in an initial quantum state [math]i[/math] to two particles ( c and d) in a final state [math]f[/math].
- a + b [math]\rightarrow[/math] c + d
where a is the incoming particle and b is the target particle.
Although Fermi first coined the term "Golden Rule", Dirac developed most of the machinery.
Let [math]\Phi[/math] represent the Flux of particle per unit time through a unit area normal to the beam. Then
- [math]\Phi = n_a v_i [/math]
where
- [math]n_a[/math] = density of particles in the incident beam
- [math]v_i[/math] = velocity of a relative to b.
The probability the incident particle will hit a target particle is given by the cross-section [math]\sigma[/math] times the number of target particles per unit area [math](n_b)[/math].
The number of interactions therefor will be given by
- Number of Interactions per unit area per unit second= [math]n_b \sigma \times \Phi
[/math]
The transition rate [math](W)[/math] per target particle [math](n_b)[/math] is
- [math]\frac{W}{n_b} = \sigma \Phi = \sigma n_a v_i[/math]
Solving the above for the Cross section \sigma we have
- [math]\sigma = \frac{W}{n_b \Phi}= \frac{W}{n_b n_a v_i}[/math]
A calculation of the transition rate W si equivalent to calculating the cross section of the scattering process.
Fermi's Golden rule says that the transition rate [math]W[/math] is given by a transition matrix element (or "Amplitude") [math]M_{i,f}[/math] weighted by the phase space and Plank's constant [math]\hbar[/math] such that
- [math]W = \frac{2 \pi}{\hbar} |M_{i,f}|^2 \times [/math](Phase Space) = \frac{0.693}{t_{1/2}}
- [math]t_{1/2} =[/math] transition half life.
Transition Amplitude
- [math]| M_{i,f}| ^2 \equiv \int \psi_f^{*}(\vec{r}) H_{int} \psi_i(\vec{r}) dr^3[/math]
where
- [math]\psi_i[/math] = initial quantum state of the system which is an eigenstate of the time independent ("steady state") Hamiltonian ([math]H_0[/math])
- [math]\psi_f[/math] = final quantum state of system after a transition
- [math]H_{int}[/math] = the part of the total Hamiltonian ([math]H_{tot}[/math]) which describes the interaction responsible for the transition.
- [math]H_0[/math] = Unperturbed ("steady state") Hamiltonian
- [math]H_{tot} = H_0 + H_{int}[/math] = total Hamiltonian describing the quantum mechanical system
- [math]dr^2[/math] integration over all space
The off diagonal elements of the [math]M_{i,f}[/math] matrix tell you the transition probablility.
Stationary State
The stationary state system is given by the solutions of the schrodinger equation for H_0
- [math]i \hbar \frac{\partial \psi_i}{\partial t} = H_0 \psi_i[/math]
- [math]\psi_i = u_n e^{-\frac{i E_n}{\hbar}t}[/math]
where
- [math]H_0 u_n = E_n u_n[/math]
- [math]E_n[/math] = energy eigen values
Interaction Hamiltonian
- [math]H_{int}[/math] = Interaction Hamiltonian = perturbation to [math]H_0[/math] which causes a transition/interaction. The time dependent schrodinger equation for this perturbation is:
- [math]i \hbar \frac{\partial \psi}{\partial t} = (H_0 + H_{int} ) \psi[/math]
One can write the solution [math]\psi[/math] in terms of a linear combination of the basis functions [math](u_n)[/math] from the Stationary State solution.
- [math]\psi = \sum_n a_n(t) u_n(x) e^{- \frac{i E_n}{\hbar}t}[/math]
You jsut need to find the components of the basis eigenfunctions (eigenvectors) using the Schrodinger equation
- [math]i \hbar \sum_n \frac{d a_n}{dt} u_n e^{- \frac{i E_n}{\hbar}t} + \sum E_n a_n u_n e^{- \frac{i E_n}{\hbar}t} = \sum_n a_n (H_0 + H_{int}) u_n e^{- \frac{i E_n}{\hbar}t}[/math]
Because
- [math]H_0 u_n = E_n u_n[/math]
The second term on the left hand side is canceled with the [math]H_0[/math] term on the right hand side
- [math]i \hbar \sum_n \frac{d a_n}{dt} u_n e^{- \frac{i E_n}{\hbar}t} = \sum_n a_n H_{int} u_n e^{- \frac{i E_n}{\hbar}t}[/math]
multiple both sides by [math]u_{n^{\prime}}^* e^{i\frac{E_{n^{\prime}}}{\hbar}t}[/math] and integrate over the whole volume
- [math] i \hbar \frac{d a_n}{dt} \delta_{n n^{\prime}}= \sum_n \lt u_{n^{\prime}} | H_{int} | u_n\gt a_n e^{- i\frac{E_{n^{\prime}}-E_n}{\hbar}t}[/math]
where
- [math]\lt u_{n^{\prime}} | H_{int} | u_n\gt = \int d^3x u_{n^{\prime}}^* H_{int} u_n[/math]
Integrate the above equation
- [math]\int_0^T \frac{d a_{n^{\prime}}}{dt} = \frac{-i}{\hbar} \int_0^T \sum_n \lt u_{n^{\prime}} | H_{int} | u_n\gt a_n e^{i\frac{E_{n^{\prime}}-E_n}{\hbar}t} dt[/math]
If we make the following assumptions
1.) The quantum state is [math]u_{\alpha}[/math] just before the particle interacts via [math]H_{int}[/math][math]\Rightarrow u_n = u_{\alpha}[/math]
2.) [math]H_{int}[/math] acts over a very small time ( strong force range is [math]10^{-15} m[/math])
3.) [math]H_{int}[/math] is so weak that the initial quantum state is not substantially altered by the interaction. Or other states are very weakly involved ([math]H_{int}[/math] prefers one state over all the others)
- [math]a_n=\left \{ {1 \;\;\;\; n= \alpha \atop 0 \;\;\;\; n \ne \alpha} \right .[/math]
= 1
Then
- [math]\sum_n \lt u_{n^{\prime}} | H_{int} | u_n\gt = \lt u_{n^{\prime}} | H_{int} | u_{\alpha}\gt [/math]
- [math]\Rightarrow a_{n^{\prime}} = \frac{-i}{\hbar} \int_0^T \lt u_{n^{\prime}} | H_{int} | u_{\alpha}\gt (1) e^{i\frac{E_{n^{\prime}}-E_{\alpha}}{\hbar}t} dt[/math]
- [math]= \frac{-i}{\hbar} \lt u_{n^{\prime}} | H_{int} | u_{\alpha}\gt \int_0^T e^{i\frac{E_{n^{\prime}}-E_{\alpha}}{\hbar}t} dt[/math]
- [math]= \frac{-i}{\hbar} \lt u_{n^{\prime}} | H_{int} | u_{\alpha}\gt \frac{\hbar}{i(E_{n^{\prime}}-E_{\alpha})}e^{i\frac{E_{n^{\prime}}-E_{\alpha}}{\hbar}t}|_0^T
[/math]
- [math]= -\frac{\lt u_{n^{\prime}} | H_{int} | u_{\alpha}\gt }{(E_{n^{\prime}}-E_{\alpha})}\left ( e^{i\frac{E_{n^{\prime}}-E_{\alpha}}{\hbar}T} -1\right )
[/math]
- [math]a_{n^{\prime}} =\frac{\lt u_{n^{\prime}} | H_{int} | u_{\alpha}\gt }{(E_{n^{\prime}}-E_{\alpha})}\left ( 1 - e^{i\frac{E_{n^{\prime}}-E_{\alpha}}{\hbar}T}\right )[/math] = amplitude for making a transition from [math]u_{\alpha}[/math] to [math]u_{n^{\prime}}[/math]
Transition Probability
The probability [math](P_{n^{\prime} \alpha} )[/math] of making a transition from t state [math]u_{\alpha}[/math] to the state [math]u_{n^{\prime}}[/math] is given by the magnitude of the amplitude [math]a_{n^{\prime}}[/math]
- [math]P_{n^{\prime} \alpha}= | a_{n^{\prime}} |^2[/math]
- [math]= \frac{|\lt u_{n^{\prime}} | H_{int} | u_{\alpha}\gt |^2}{(E_{n^{\prime}}-E_{\alpha})^2}\left ( 1 - e^{i\frac{E_{n^{\prime}}-E_{\alpha}}{\hbar}T}\right ) \left ( 1 - e^{-i\frac{E_{n^{\prime}}-E_{\alpha}}{\hbar}T}\right )
[/math]
- [math]= \frac{|\lt u_{n^{\prime}} | H_{int} | u_{\alpha}\gt |^2}{(E_{n^{\prime}}-E_{\alpha})^2} 4 \sin^2 \left(\frac{E_{n^{\prime}}-E_{\alpha}}{2\hbar}T \right )[/math]
- [math]e^{\pm ix} = \cos(x) \pm i \sin(x)[/math] and [math]\cos(\theta) = 1 - 2 \sin^2(\theta/2)[/math]
What does this probability function look like?
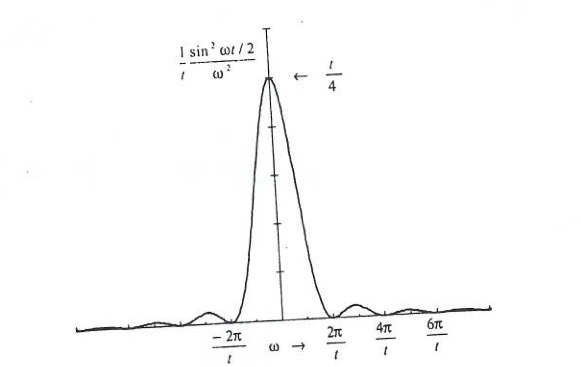
- Notice
- The probability of a transition gets smaller if the energy difference between the state [math]( E_{n^{\prime}}-E_{\alpha})[/math] gets bigger.
- It illustrates the uncertainty principle [math]\Delta E \Delta t \gt \hbar[/math]. [math]\Delta w[/math] is the Half Width of the peak. In the above picture [math]\Delta w t \approx \pi[/math].
- Another indication of the uncertainty principle is oberved if you let [math]t \rightarrow \infty[/math] then above function goes to a delta function [math](\frac{\pi}{2}\delta(w))[/math]
- For [math]\Delta E \equiv \frac{2 \pi \hbar}{T}[/math] Most of the above function lies in the interval [math][(E_{\alpha} - \Delta E ),(E_{\alpha} + \Delta E )][/math]
The probability of transition (The total transition probability to all states) is given by adding up all the probabilities to individual states.
- [math]P = \sum_{n^{\prime}} P_{n^{\prime} \alpha}[/math]
- [math]= 4 \sum_{n^{\prime}} \frac{|\lt u_{n^{\prime}} | H_{int} | u_{\alpha}\gt |^2}{(E_{n^{\prime}}-E_{\alpha})^2} \sin^2 \left(\frac{E_{n^{\prime}}-E_{\alpha}}{2\hbar}T \right )[/math]
If we assume the states are all clustered together as in a continuum then
- [math]|\lt u_{n^{\prime}} | H_{int} | u_{\alpha}\gt |^2 =[/math] constant [math]\equiv |\lt \beta | H_{int} | \alpha\gt |^2[/math]
This assumption isn't so bad when you realize that since the above function lies over a finite energy interval and that that finite energy interval contains similar states.
Since we assume a continuum the summation becomes an integral such that
- [math]P(T) = 4 |\lt \beta | H_{int} | \alpha\gt |^2 \int \frac{\sin^2 \left(\frac{E(N)-E_{\alpha}}{2\hbar}T \right )}{(E(N)-E_{\alpha})^2} dN[/math]
Where the Energy [math](E)[/math] is an explicit function of state number [math]N[/math].
Using the chain rule we can recast the integral
let
- [math]x \equiv \frac{(E(N)-E_{\alpha})T}{2\hbar}[/math]
Then
- [math]dx = \frac{T}{2 \hbar} dE(N)[/math]
and
- [math]dN = \frac{dN}{dE} dE = \frac{dN}{dE} \frac{2 \hbar}{T} dx[/math]
- [math]P(T) = 4 |\lt \beta | H_{int} | \alpha\gt |^2 \frac{dN}{dE} \frac{T}{2 \hbar} \int_{-\infty}^{\infty} \frac{\sin^2 (x)}{(x)^2} dx[/math]
- [math]\int_{-\infty}^{\infty} \frac{\sin^2 (x)}{(x)^2} dx = \pi[/math]
- [math]P(T) = \frac{2 \pi T}{ \hbar}|\lt \beta | H_{int} | \alpha\gt |^2 \frac{dN}{dE} [/math]
- [math]P|\lt \beta | H_{int} | \alpha\gt |^2 [/math] =:[math]| M_{i,f}| ^2 \equiv \int \psi_f^{*}(\vec{r}) H_{int} \psi_i(\vec{r}) dr^3[/math]
- [math]\frac{dN}{dE} = [/math] Density of states[math] ( \rho(\alpha))[/math]
Single Particle decay
Consider the case when a single particle decays into multiple fragments (several other particles)
- [math]d \Gamma = \hbar W = | M |^2 \frac{S}{2 \hbar m_1} \left [ \left ( \frac{d^3\vec{p}_2}{(2 \pi)^3 2E_2} \right )\left ( \frac{d^3\vec{p}_3}{(2 \pi)^3 2E_3} \right )\left ( \frac{d^3\vec{p}_4}{(2 \pi)^3 2E_4} \right ) \cdots \left ( \frac{d^3\vec{p}_N}{(2 \pi)^3 2E_N} \right ) \right ] \times (2 \pi)^4 \delta^4(p_1^\mu-p_2^\mu-p_3^\mu- \cdots p_n^\mu)[/math]
where
- [math]W[/math] = probability per second that the particle will decay
- [math]S[/math] = a symmetry factor of [math]\left( \frac{1}{j!}\right )[/math] for every group of [math]j[/math] identical particles in the final state
- [math]p_i^\mu = (E_i, \vec{p}_i) [/math]= 4-momentum of the [math]i^{th}[/math] particle. ;[math] p_1 = (E_1,0)[/math]
- [math]\delta^4(p_1-p_2-p_3- \cdots p_n)[/math] = conservation of 4-momentum
- Note
- [math]\int \frac{d^3 \vec{p}_i}{2E_i} = \int d^4p_i \delta(p_i^2-m_i^2)[/math] = invariant under Lorentz transformations
Example: Pi-zero ([math]\pi^0[/math]) decay
- [math]\pi^0 \rightarrow \gamma + \gamma[/math]
we are interested in calculating
- [math]d \Gamma = \hbar W = | M |^2 \frac{S}{2 \hbar m_1} \left [ \left ( \frac{d^3\vec{p}_2}{(2 \pi)^3 2E_2} \right )\left ( \frac{d^3\vec{p}_3}{(2 \pi)^3 2E_3} \right ) \right ] (2 \pi)^4 \delta^4(p_1^\mu-p_2^\mu-p_3^\mu)[/math]
Consider the decay of a neutral pion ([math]\pi^0[/math]) into two photons ([math]\gamma[/math]).
The two gammas are identical particles so
- [math]S = \frac{1}{2!} = \frac{1}{1 \cdot 2} = \frac{1}{2}[/math]
Since the pion is initially at rest (or we can go to its rest frame and then Lorentz boost back to the lab frame)
- [math]p_1^\mu = (E_1,p_1) = (E_1,0) = (m_{\pi^0},0)[/math]
Because photons have no mass, [math]m_2=m_3 = 0[/math] :
- [math]p_2^\mu = (E_2,\vec{p}_2) = (|\vec{p}_2|,\vec{p}_2) = (p_2,\vec{p}_2)[/math]
- [math]p_3^\mu = (E_3,\vec{p}_3) = (|\vec{p}_3|,\vec{p}_3)= (p_3,\vec{p}_3)[/math]
- [math]\delta^4(p_1^\mu-p_2^\mu-p_3^\mu) = \delta(m_{\pi} -p_2-p_3) \delta(0-\vec{p}_2 - \vec{p}_3)[/math]
- [math]\int d \Gamma = \int \frac{|M|^2}{16 (2 \pi)^6 \hbar m_{\pi} }\left [ \left ( \frac{d^3\vec{p}_2}{E_2} \right )\left ( \frac{d^3\vec{p}_3}{E_3} \right ) \right ] (2 \pi)^4 \delta(m_{\pi} -p_2-p_3) \delta(0-\vec{p}_2 - \vec{p}_3)[/math]
- [math]= \int \frac{|M|^2}{(8 \pi)^2 \hbar m_{\pi} }\left [ \left ( \frac{d^3\vec{p}_2}{E_2} \right )\left ( \frac{d^3\vec{p}_3}{E_3} \right ) \right ] \delta(m_{\pi} -p_2-p_3) \delta(0-\vec{p}_2 - \vec{p}_3)[/math]
- [math]= \int \frac{|M|^2}{(8 \pi)^2 \hbar m_{\pi}p_2 p_3 }\left [ \left ( d^3\vec{p}_2 \right )\left ( d^3\vec{p}_3 \right ) \right ] \delta(m_{\pi} -p_2-p_3) \delta(0-\vec{p}_2 - \vec{p}_3)[/math]
Integrating over[math] d^3\vec{p}_3 \Rightarrow \vec{p}_2 = - \vec{p}_3 , | p_2| = |p_3|[/math] :
- [math]\int d \Gamma = \int \frac{|M|^2}{(8 \pi)^2 \hbar m_{\pi} p_2^2}\left [ \left ( d^3\vec{p}_2 \right ) \right ] \delta(m_{\pi} -2p_2) [/math]
- [math]= \int \frac{|M|^2}{(8 \pi)^2 \hbar m_{\pi} p_2^2}\left [ \left ( |\vec{p}_2|^2 d|\vec{p}_2| \sin(\theta) d \theta d \phi \right ) \right ] \delta(m_{\pi} -2p_2)[/math]
If [math]|M|^2 = f( \vec{p}_2) \ne f( \vec{p}_2,\vec{p}_3)[/math]( the transition does not depend on the momentum vector directions)
then
- [math]\int d \Gamma = \frac{|M|^2}{(8 \pi)^2 \hbar m_{\pi}}\int \frac{1}{ p_2^2}\left [ \left ( |\vec{p}_2|^2 d|\vec{p}_2| \sin(\theta) d \theta d \phi \right ) \right ] \delta(m_{\pi} -2p_2)[/math]
- [math]= \frac{1}{(8 \pi)^2 \hbar m_{\pi}}\int |M|^2\delta(m_{\pi} -2p_2) d|\vec{p}_2| \sin(\theta) d \theta d \phi [/math]
- [math]= \frac{1}{(8 \pi)^2 \hbar m_{\pi}} (4 \pi) \int |M|^2 \delta(m_{\pi} -2p_2) d|\vec{p}_2| [/math]
- [math]= \frac{1}{(16 \pi) \hbar m_{\pi}} \int |M|^2\delta(m_{\pi} -2p_2) d|\vec{p}_2| [/math]
- [math]= \frac{|M|^2}{(16 \pi) \hbar m_{\pi}} \frac{1}{2} \;\; : \delta (kx) = \frac{\delta(x)}{k} \Rightarrow \delta (m_{\pi} -2p_2)=\frac{\delta (\frac{m_{\pi}}{2} -p_2)}{2} [/math]
- [math] \Gamma= \frac{|M|^2}{(32 \pi) \hbar m_{\pi}} [/math] with the additional conditions that [math]p_2 = \frac{m_{\pi}}{2}[/math]and [math]\vec{p}_2 = - \vec{p}_3[/math] which must be applied when evaluating[math] |M|^2[/math]
- Units check
- [math]\hbar m_{\pi} = \left ( 6.582 \times 10^{-10} MeV \cdot s\right ) (150 MeV) = 9.97 \times 10^{-8} MeV^2 \cdot s[/math]
- [math]\left [ |M|^2\right ] = MeV^2 [/math]= energy eigenvalues squared
- [math] \left [ \Gamma \right ] = \frac{MeV^2 }{MeV^2 \cdot s} = \frac{1}{s} =[/math] transition probability per unit time
- Caveat
- Sometimes [math]|M|[/math] will depend on the momentum vector directions in which case the integral must be done after evaluating the matrix element amplitude. An example of this is when the transition is spin dependent [math](\vec{p} \cdot \vec{s})[/math] as in the hyperfine interaction or polarization based transitions.
Example: Two -Body decay (fission fragments)
Now consider a more general case in which the decay daughters have mass:
- [math]d \Gamma = \hbar W = | M |^2 \frac{S}{2 \hbar m_1} \left [ \left ( \frac{d^3\vec{p}_2}{(2 \pi)^3 2E_2} \right )\left ( \frac{d^3\vec{p}_3}{(2 \pi)^3 2E_3} \right ) \right ] (2 \pi)^4 \delta^4(p_1^\mu-p_2^\mu-p_3^\mu)[/math]
We don't know if the two daughter particles are identical so leave [math]S[/math] as a funtion.
- [math]S = ?[/math]
We can still do the calculation in the mother particles rest frame.
- [math]p_1^\mu = (E_1,p_1) = (E_1,0) = (m_1,0)[/math]
Now that the daughters have mass we need:
- [math]p_2^\mu = (E_2,\vec{p}_2) \; E_2 = \sqrt{p_2^2 + m_2^2}[/math]
- [math]p_3^\mu = (E_3,\vec{p}_3) \; E_3 = \sqrt{p_3^2 + m_3^2}[/math]
- [math]\int d \Gamma = \int \frac{S|M|^2}{8 (2 \pi)^6 \hbar m_1 }\left [ \left ( \frac{d^3\vec{p}_2}{E_2} \right )\left ( \frac{d^3\vec{p}_3}{E_3} \right ) \right ] (2 \pi)^4 \delta(m_1 -p_2-p_3) \delta(0-\vec{p}_2 - \vec{p}_3)[/math]
Recast the delta function:
- [math]\delta^4(p_1^\mu-p_2^\mu-p_3^\mu) = \delta(m_1 -E_2-E_3) \delta(0-\vec{p}_2 - \vec{p}_3)[/math]
Upon integrating over [math]d^3 \vec{p}_3[/math]
- [math]\delta(0-\vec{p}_2 - \vec{p}_3) \Rightarrow |\vec{p}_2| = | \vec{p}_3| \Rightarrow E_3 = \sqrt{p_3^2 + m_3^2} = E_3 = \sqrt{p_2^2 + m_3^2}[/math]
- [math]\delta^4(p_1^\mu-p_2^\mu-p_3^\mu) = \delta(m_1 -\sqrt{p_2^2 + m_2^2} - \sqrt{p_2^2 + m_3^2}) [/math]
After integrating over [math]d^3 \vec{p}_3[/math] the delta function gives you
- [math]\int d \Gamma = \int \frac{S|M|^2}{8 (2 \pi)^2 \hbar m_1 }\left [ \left ( \frac{d^3\vec{p}_2}{E_2 \sqrt{p_2^2 + m_3^2}} \right ) \right ] \delta(m_1 -\sqrt{p_2^2 + m_2^2} - \sqrt{p_2^2 + m_3^2}) [/math]
Once again , if the transition amplitude does not depend on the vector directions of[math] \vec{p}_2[/math] and [math]\vec{p}_3[/math] then you can integrate over angles [math](\theta , \phi)[/math] and get a [math]4 \pi[/math].
- [math]\int d \Gamma = \frac{S}{8 \pi \hbar m_1 } \int \left [ \left ( |M|^2 |\vec{p}_2|^2 \frac{d |\vec{p}_2| }{E_2 \sqrt{p_2^2 + m_3^2}} \right ) \right ] \delta(m_1 -\sqrt{p_2^2 + m_2^2} - \sqrt{p_2^2 + m_3^2}) [/math]
Let
- [math]E_{tot} \equiv \sqrt{p_2^2 + m_2^2} + \sqrt{p_3^2 + m_3^2} = \sqrt{p_2^2 + m_2^2} + \sqrt{p_2^2 + m_3^2}[/math]
Then
- [math]d E_{tot} = \frac{E_{tot} p_2 d p_2}{ \sqrt{p_2^2 + m_2^2} \sqrt{p_2^2 + m_3^2}}[/math]
substituting
- [math]\Gamma = \frac{S}{8 \pi \hbar m_1 } \int |M|^2 \frac{p_2}{E_{tot}} \delta(m_1 -E_{tot}) d E_{tot}[/math]
- [math]= \frac{S}{8 \pi \hbar m_1 } |M|^2 \frac{p_2}{E_{tot}} [/math]
where [math]E_{tot} = m_1[/math]
and
[math]p_2[/math] = momentum when [math]E_{tot} = m_1 = \sqrt{p_2^2 + m_2^2} + \sqrt{p_2^2 + m_3^2}[/math]
or
- [math]p_2 = \frac{1}{2m_1} \sqrt{m_1^4 + m_2^4 + m_3^4 - 2m_1^2m_2^2 - 2m_2^2m_3^2 - 2m_3^2m_1^2}[/math]
- [math]\Gamma = \frac{S}{8 \pi \hbar m_1^2 } |M|^2 \frac{1}{2m_1} \sqrt{m_1^4 + m_2^4 + m_3^4 - 2m_1^2m_2^2 - 2m_2^2m_3^2 - 2m_3^2m_1^2}[/math]
2 Body scattering in CM frame
Lets consider the case when two particles ( [math]m_1[/math] and [math]m_2[/math]) collide and are transformed into two separate particle ([math]m_3[/math] and [math]m_4[/math]). An interaction happens during the collision which changes the two particles into two other particles.
Calculate the differential cross section, in the center of momentum frame, assuming that [math]|M|[/math] is the amplitude for this collision.
The general expression for the cross section via Fermi's golden rule is similar to the above pion decay example if you consider m_1 and m_2 forming an intermediate state and is given as
- [math]d^2 \sigma = \left( \frac{\hbar }{8 \pi}\right )^2 \frac{S |M|^2}{\sqrt{ \left [ \left ( p_1 \right )_{\mu} \left ( p_2\right )^{\mu})\right ]^2 - (m_1 m_2)^2}} \left [ \left ( \frac{d^3p_3}{E_3}\right) \left ( \frac{d^3p_4}{E_4}\right) \right ] \delta^4(p_1^{\mu}+p_2^{\mu}-p_3^{\mu}-p_4^{\mu})[/math]
In the CM frame
- [math]\vec{p}_1 = -\vec{p}_2[/math]
[math]\left ( p_1 \right )_{\mu} \left ( p_2\right )^{\mu}[/math]
- [math]= (E_1,-\vec{p}_1)\cdot (E_2,\vec{p}_2)[/math]
- [math]= E_1E_2 -\vec{p_1} \cdot \vec{p}_2 [/math]
- [math]= E_1 E_2 + p_1^2[/math]
[math] \left [ \left ( p_1 \right )_{\mu} \left ( p_2\right )^{\mu})\right ]^2= \left [ E_1E_2 + p_1^2 \right ] ^2[/math]
- [math]= (E_1^2E_2^2 + 2 E_1 E_2p_1^2 + p_1^4[/math]
- [math]=\left [ \sqrt{p_1^2 + m_1^2}\sqrt{p_1^2 + m_2^2} \right ]^2 + p_1^4 + 2 E_1E_2p_1^2[/math]
- [math]= p_1^4 + (m_1 + m_2)p_1^2 + (m_1m_2)^2 + p_1^4 + 2E_1E_2p_1^2[/math]
- [math]= (p_1^2 + m_1^2 + p_1^2 + m_2^2)p_1^2 + (m_1 m_2)^2 + 2E_1E_2p_1^2[/math]
- [math]= (E_1^2 + E_2^2)p_1^2 + 2E_1E_2 + (m_1 m_2)^2[/math]
- [math]= (E_1 + E_2)^2p_1^2 +(m_1 m_2)^2[/math]
- [math]\left [ \left ( p_1 \right )_{\mu} \left ( p_2\right )^{\mu})\right ]^2= (E_1 + E_2)^2p_1^2 +(m_1 m_2)^2[/math]
or
- [math]\sqrt{ \left [ \left ( p_1 \right )_{\mu} \left ( p_2\right )^{\mu})\right ]^2 - (m_1 m_2)^2}= (E_1 + E_2)p_1 [/math]
substituting the above and
- [math]\delta^4(p_1^{\mu}+p_2^{\mu}-p_3^{\mu}-p_4^{\mu})=\delta(E_1+E_2-E_3-E_4) \delta^3(\vec{p}_1 + \vec{p}_2 - \vec{p}_3 - \vec{p}_4)[/math]
- [math]= \delta(E_1+E_2-E_3-E_4) \delta^3( -\vec{p}_3 - \vec{p}_4)[/math] : [math]\vec{p}_1 =- \vec{p}_2[/math]
into the cross ection equation we have
- [math]d^2 \sigma = \left( \frac{\hbar }{8 \pi}\right )^2 \frac{S |M|^2}{(E_1 + E_2)p_1} \left [ \left ( \frac{d^3p_3}{E_3}\right) \left ( \frac{d^3p_4}{E_4}\right) \right ] \delta(E_1+E_2-E_3-E_4) \delta^3( -\vec{p}_3 - \vec{p}_4)[/math]
integrating over [math]d^3 \vec{p}_4[/math] we have
- [math]\int \int d^2\sigma = \int \int \left( \frac{\hbar }{8 \pi}\right )^2 \frac{S |M|^2}{(E_1 + E_2)p_1} \left [ \left ( \frac{d^3p_3}{E_3}\right) \left ( \frac{d^3p_4}{E_4}\right) \right ] \delta(E_1+E_2-E_3-E_4) \delta^3( -\vec{p}_3 - \vec{p}_4)[/math]
- [math]=\int \int \left( \frac{\hbar }{8 \pi}\right )^2 \frac{S |M|^2}{(E_1 + E_2)p_1} \left [ \left ( \frac{d^3p_3}{E_3}\right) \left ( \frac{d^3p_4}{\sqrt{p_4^2 + m_4^2}}\right) \right ] \delta(E_1+E_2-E_3-\sqrt{p_4^2 + m_4^2}) \delta^3( -\vec{p}_3 - \vec{p}_4)[/math]
- [math]=\int \left( \frac{\hbar }{8 \pi}\right )^2 \frac{S |M|^2}{(E_1 + E_2)p_1} \left [ \left ( \frac{d^3p_3}{E_3}\right) \left ( \frac{1}{\sqrt{p_3^2 + m_4^2}}\right) \right ] \delta(E_1+E_2-E_3-\sqrt{p_3^2 + m_4^2}) [/math]
Unfortunately [math]|M|^2[/math] depends on scattering angles. For some interactions it even depends on [math]\phi[/math] angles (5th structure function, single spin asymmetries).
If you write the cross section in terms of a differential cross section in solid angle [math]\left ( d \Omega \equiv sin (\theta) d \theta d \phi \right )[/math] then only the momentum part of the integral remains.
- [math]\frac{ d \sigma}{d \Omega}=\int \left( \frac{\hbar }{8 \pi}\right )^2 \frac{S |M|^2}{(E_1 + E_2)p_1} \left [ \left ( \frac{p_3^2 d p_3}{E_3}\right) \left ( \frac{1}{\sqrt{p_3^2 + m_4^2}}\right) \right ] \delta(E_1+E_2-E_3-\sqrt{p_3^2 + m_4^2}) [/math]
- [math]=\left( \frac{\hbar }{8 \pi}\right )^2 \frac{S}{(E_1 + E_2)p_1} \int \frac{|M|^2 p_3^2 }{E_3\sqrt{p_3^2 + m_4^2}} \delta(E_1+E_2-E_3-\sqrt{p_3^2 + m_4^2})d p_3 [/math]
This integral looks just like the 2-Body decay problem if you let [math]m_1 = E_1 + E_2[/math]
- [math]\frac{ d \sigma}{d \Omega}=\left( \frac{\hbar }{8 \pi}\right )^2 \frac{S}{(E_1 + E_2)p_1} \frac{|M|^2 p_3 }{E_1+E_2}[/math]
- [math]=\left( \frac{\hbar }{8 \pi}\right )^2 \frac{S}{(E_1 + E_2)^2} \frac{|M|^2 p_3 }{p_1}[/math]
- [math]=\left( \frac{\hbar }{8 \pi}\right )^2 \frac{S|M|^2}{(E_1 + E_2)^2} \frac{ p_3 }{p_1}[/math]
Note: In Center of Momentum frame [math]|\vec{p}_1| = |\vec{p}_2|[/math] and [math]|\vec{p}_3| =|\vec{p}_4|[/math]
so
- [math]\frac{ d \sigma}{d \Omega} \left( \frac{\hbar }{8 \pi}\right )^2 \frac{S|M|^2}{(E_1 + E_2)^2} \frac{ p_f }{p_i}[/math]
where [math]p_f = |\vec{p}_3| = |\vec{p}_4|[/math] and [math]p_i = |\vec{p}_1| = |\vec{p}_2|[/math]
- Units
- Notice that the number of integrals is equal to the number of particles in the interaction. The units of [math]|M|^2[/math] change with the number of integrals [math](n)[/math] such that [math][|M|^2] = \left (\frac{MeV}{c}\right)^{4-n}[/math]
Back to Classes Classes
