Difference between revisions of "Forest Error Analysis for the Physical Sciences"
| Line 429: | Line 429: | ||
40% Grammatically correct written explanation of the data analysis with publication quality plots | 40% Grammatically correct written explanation of the data analysis with publication quality plots | ||
| − | Report due in my office and source code in my e-mail by Friday, May | + | Report due in my office and source code in my e-mail by Friday, May 8, 2:30 pm (MST) |
Report length is between 3 and 15 pages all inclusive. Min Font Size is 12 pt, 1.5 spacing of lines, max margin 2". | Report length is between 3 and 15 pages all inclusive. Min Font Size is 12 pt, 1.5 spacing of lines, max margin 2". | ||
Latest revision as of 22:11, 29 April 2020
Class Admin
Forest_ErrorAnalysis_Syllabus
Homework
Homework is due at the beginning of class on the assigned day. If you have a documented excuse for your absence, then you will have 24 hours to hand in the homework after being released by your doctor.
Class Policies
http://wiki.iac.isu.edu/index.php/Forest_Class_Policies
Instructional Objectives
- Course Catalog Description
- Error Analysis for the Physics Sciences 3 credits. Lecture course with computation requirements. Topics include: Error propagation, Probability Distributions, Least Squares fit, multiple regression, goodness of fit, covariance and correlations.
Prequisites:Math 360.
- Course Description
- The application of statistical inference and hypothesis testing will be the main focus of this course for students who are senior level undergraduates or beginning graduate students. The course begins by introducing the basic skills of error analysis and then proceeds to describe fundamental methods comparing measurements and models. A freely available data analysis package known as ROOT will be used. Some programming skills will be needed using C/C++ but a limited amount of experience is assumed.
Objectives and Outcomes
Forest_ErrorAnalysis_ObjectivesnOutcomes
Suggested Text
Data Reduction and Error Analysis for the Physical Sciences by Philip Bevington ISBN: 0079112439
Homework
Class Labs
Systematic and Random Uncertainties
Although the name of the class is "Error Analysis" for historical purposes, a more accurate description would be "Uncertainty Analysis". "Error" usually means a mistake is made while "Uncertainty" is a measure of how confident you are in a measurement.
Accuracy -vs- Precision
- Accuracy
- How close does an experiment come to the correct result
- Precision
- A measure of how exact the result is determined. No reference is made to what the result means.
Systematic Error
What is a systematic error?
A class of errors which result in reproducible mistakes due to equipment bias or a bias related to its use by the observer.
Example: A ruler
a.) A ruler could be shorter or longer because of temperature fluctuations
b.) An observer could be viewing the markings at a glancing angle.
In this case a systematic error is more of a mistake than an uncertainty.
In some cases you can correct for the systematic error. In the above Ruler example you can measure how the ruler's length changes with temperature. You can then correct this systematic error by measuring the temperature of the ruler during the distance measurement.
Correction Example:
A ruler is calibrated at 25 C an has an expansion coefficient of (0.0005 0.0001 m/C.
You measure the length of a wire at 20 C and find that on average it is m long.
This means that the 1 m ruler is really (1-(20-25 C)(0.0005 m/C)) = 0.99775
So the correction becomes
1.982 *( 0.99775) =1.977 m
- Note
- The numbers above without decimal points are integers. Integers have infinite precision. We will discuss the propagation of the errors above in a different chapter.
Error from bad technique:
After repeating the experiment several times the observer discovers that he had a tendency to read the meter stick at an angle and not from directly above. After investigating this misread with repeated measurements the observer estimates that on average he will misread the meter stick by 2 mm. This is now a systematic error that is estimated using random statistics.
Reporting Uncertainties
Notation
X Y = X(Y)
Significant Figures and Round off
Significant figures
- Most Significant digit
- The leftmost non-zero digit is the most significant digit of a reported value
- Least Significant digit
- The least significant digit is identified using the following criteria
- 1.) If there is no decimal point, then the rightmost digit is the least significant digit.
- 2.)If there is a decimal point, then the rightmost digit is the least significant digit, even if it is a zero.
In other words, zero counts as a least significant digit only if it is after the decimal point. So when you report a measurement with a zero in such a position you had better mean it.
- The number of significant digits in a measurement are the number of digits which appear between the least and most significant digits.
examples:
| Measurement | most Sig. digit | least Sig. | Num. Sig. Dig. | Scientific Notation |
| 5 | 5 | 5 | 1* | |
| 5.0 | 5 | 0 | 2 | |
| 50 | 5 | 0 | 2* | |
| 50.1 | 5 | 1 | 3 | |
| 0.005001 | 5 | 1 | 4 |
- Note
- The values of "5" and "50" above are ambiguous unless we use scientific notation in which case we know if the zero is significant or not. Otherwise, integers have infinite precision.
Round Off
Measurements that are reported which are based on the calculation of more than one measured quantity must have the same number of significant digits as the quantity with the smallest number of significant digits.
To accomplish this you will need to round of the final measured value that is reported.
To round off a number you:
1.) Increment the least significant digit by one if the digit below it (in significance) is greater than 5.
2.) Do nothing if the digit below it (in significance) is less than 5.
Then truncate the remaining digits below the least significant digit.
- What happens if the next significant digit below the least significant digit is exactly 5?
To avoid a systematic error involving round off you would ideally randomly decide to just truncate or increment. If your calculation is not on a computer with a random number generator, or you don't have one handy, then the typical technique is to increment the least significant digit if it is odd (or even) and truncate it if it is even (or odd).
- Examples
The table below has three entries; the final value calculated from several measured quantities, the number of significant digits for the measurement with the smallest number of significant digits, and the rounded off value properly reported using scientific notation.
| Value | Sig. digits | Rounded off value |
| 12.34 | 3 | |
| 12.36 | 3 | |
| 12.35 | 3 | |
| 12.35 | 2 |
Statistics abuse
http://www.worldcat.org/oclc/28507867
http://www.worldcat.org/oclc/53814054
Statistical Distributions
Propagation of Uncertainties
Statistical inference
http://arxiv.org/abs/1506.09077
Byron Roe (Submitted on 30 Jun 2015)
The problem of fitting an event distribution when the total expected number of events is not fixed, keeps appearing in experimental studies. In a chi-square fit, if overall normalization is one of the parameters parameters to be fit, the fitted curve may be seriously low with respect to the data points, sometimes below all of them. This problem and the solution for it are well known within the statistics community, but, apparently, not well known among some of the physics community. The purpose of this note is didactic, to explain the cause of the problem and the easy and elegant solution. The solution is to use maximum likelihood instead of chi-square. The essential difference between the two approaches is that maximum likelihood uses the normalization of each term in the chi-square assuming it is a normal distribution, 1/sqrt(2 pi sigma-square). In addition, the normalization is applied to the theoretical expectation not to the data. In the present note we illustrate what goes wrong and how maximum likelihood fixes the problem in a very simple toy example which illustrates the problem clearly and is the appropriate physics model for event histograms. We then note how a simple modification to the chi-square method gives a result identical to the maximum likelihood method.
References
1.) "Data Reduction and Error Analysis for the Physical Sciences", Philip R. Bevington, ISBN-10: 0079112439, ISBN-13: 9780079112439
CPP programs for Bevington
2.)An Introduction to Error Analysis, John R. Taylor ISBN 978-0-935702-75-0
3.) ROOT: An Analysis Framework
4.) Orear, "Notes on Statistics for Physicists"
5.) Statistical Methods for Engineers and Scientists, Robert M. Bethea, Benjamin S. Duran, and Thomas L. Boullion, Marcel Dekker Inc, New York, (1985), QA 276.B425
6.) Data Analysis for Scientists and Engineers, Stuart L. Meyer, John Wiley & Sons Inc, New York, (1975), QA 276.M437
7.) Syntax for ROOT Math Functions
http://root.cern.ch/root/htmldoc/MATH_Index.html
ROOT comands
A ROOT Primer
Download
You can usually download the ROOT software for multiple platforms for free at the URL below
There is a lot of documentation which may be reached through the above URL as well
some things that may need to be installed
sudo apt-get install git
sudo apt-get install make
sudo apt-get install libx11-dev
sudo apt-get install libxpm-dev
sudo apt-get install libxft-dev
sudo apt-get install libxext-dev
install
git clone http://github.com/root-project/root.git
cd root
git checkout -b v6-10-08 v6-10-08
cd ..
mkdir v6-10-08
cd v6-10-08
cmake -D mysql:BOOL=OFF ../root
cmake --build .
Setup the environment
There is an environmental variable which is usually needed on most platforms in order to run ROOT. I will just give the commands for setting things up under the bash shell running on the UNIX platform.
- Set the variable ROOTSYS to point to the directory used to install ROOT
export ROOTSYS=~/src/ROOT/root
OR
source ~/src/ROOT/root/bin/thisroot.sh
I have installed the latest version of ROOT in the subdirectory ~/src/ROOT/root.
You can now run the program from any subdirectory with the command
$ROOTSYS/bin/root
If you want to compile programs which use ROOT libraries you should probably put the "bin" subdirectory under ROOTSYS in your path as well as define a variable pointing to the subdirectory used to store all the ROOT libraries (usually $ROOTSYS/lib).
PATH=$PATH:$ROOTSYS/bin
export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:$ROOTSYS/lib
Other UNIX shell and operating systems will have different syntax for doing the same thing.
Starting and exiting ROOT
Starting and exiting the ROOT program may be the next important thing to learn.
As already mentioned above you can start ROOT by executing the command
$ROOTSYS/bin/root
from an operating system command shell. You will see a "splash" screen appear and go away after a few seconds. Your command shell is now a ROOT command interpreter known as CINT which has the command prompt "root[0]". You can type commands within this environment such as the command below to exit the ROOT program.
To EXIT the program just type
.q
Starting the ROOT Browser (GUI)
By now most computer users are accustomed to Graphical User Interfaces (GUIs) for application. You can launch a GUI from within the ROOT command interpreter interface with the command
new TBrowser();
A window should open with pull down menus. You can now exit root by selecting "Quit ROOT" from the pull down menu labeled "File" in the upper left part of the GUI window.
plotting Probability Distributions in ROOT
http://project-mathlibs.web.cern.ch/project-mathlibs/sw/html/group__PdfFunc.html
The Binomial distribution is plotted below for the case of flipping a coin 60 times (n=60,p=1/2)
- You can see the integral , Mean and , RMS by right clicking on the Statistics box and choosing "SetOptStat". A menu box pops up and you enter the binary code "1001111" (without the quotes).
root [0] Int_t i;
root [1] Double_t x
root [2] TH1F *B30=new TH1F("B30","B30",100,0,100)
root [3] for(i=0;i<100;i++) {x=ROOT::Math::binomial_pdf(i,0.5,60);B30->Fill(i,x);}
root [4] B30->Draw();
You can continue creating plots of the various distributions with the commands
root [2] TH1F *P30=new TH1F("P30","P30",100,0,100)
root [3] for(i=0;i<100;i++) {x=ROOT::Math::poisson_pdf(i,30);P30->Fill(i,x);}
root [4] P30->Draw("same");
root [2] TH1F *G30=new TH1F("G30","G30",100,0,100)
root [3] for(i=0;i<100;i++) {x=ROOT::Math::gaussian_pdf(i,3.8729,30);G30->Fill(i,x);}
root [4] G30->Draw("same");
The above commands created the plot below.
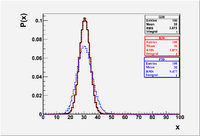 File:Forest EA BinPosGaus Mean30.eps
File:Forest EA BinPosGaus Mean30.eps
- Note
- I set each distribution to correspond to a mean () of 30. The of the Binomial distribution is = 60(1/2)(1/2) = 15. The of the Poisson distribution is defined to equal the mean . I intentionally set the mean and sigma of the Gaussian to agree with the Binomial. As you can see the Binomial and Gaussian lay on top of each other while the Poisson is wider. The Gaussian will lay on top of the Poisson if you change its to 5.477
for(i=0;i<100;i++) {x=ROOT::Math::gaussian_pdf(i,5.477,30);G30->Fill(i,x);}
- Also Note
- The Gaussian distribution can be used to represent the Binomial and Poisson distributions when the average is large ( ie:). The Poisson distribution, though, is an approximation to the Binomial distribution for the special case where the average number of successes is small ( because )
Int_t i;
Double_t x
TH1F *B30=new TH1F("B30","B30",100,0,10);
TH1F *P30=new TH1F("P30","P30",100,0,10);
for(i=0;i<10;i++) {x=ROOT::Math::binomial_pdf(i,0.1,10);B30->Fill(i,x);}
for(i=0;i<10;i++) {x=ROOT::Math::poisson_pdf(i,1);P30->Fill(i,x);}
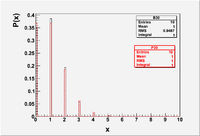 File:Forest EA BinPos Mean1.eps
File:Forest EA BinPos Mean1.eps
Other probability distribution functions
double beta_pdf(double x, double a, double b) double binomial_pdf(unsigned int k, double p, unsigned int n) double breitwigner_pdf(double x, double gamma, double x0 = 0) double cauchy_pdf(double x, double b = 1, double x0 = 0) double chisquared_pdf(double x, double r, double x0 = 0) double exponential_pdf(double x, double lambda, double x0 = 0) double fdistribution_pdf(double x, double n, double m, double x0 = 0) double gamma_pdf(double x, double alpha, double theta, double x0 = 0) double gaussian_pdf(double x, double sigma = 1, double x0 = 0) double landau_pdf(double x, double s = 1, double x0 = 0.) double lognormal_pdf(double x, double m, double s, double x0 = 0) double normal_pdf(double x, double sigma = 1, double x0 = 0) double poisson_pdf(unsigned int n, double mu) double tdistribution_pdf(double x, double r, double x0 = 0) double uniform_pdf(double x, double a, double b, double x0 = 0)
Sampling from Prob Dist in ROOT
You can also use ROOT to generate random numbers according to a given probability distribution.
In the example generates 1000 random numbers from a Poisson Parent population with a mean of 10
root [0] TRandom r
root [1] TH1F *P10=new TH1F("P10","P10",100,0,100)
root [2] for(i=0;i<10000;i++) P10->Fill(r.Poisson(30));
Warning: Automatic variable i is allocated (tmpfile):1:
root [3] P10->Draw();
Other possibilities
Gaussian with a mean of 30 and sigma of 5
root [1] TH1F *G10=new TH1F("G10","G10",100,0,100)
root [2] for(i=0;i<10000;i++) G10->Fill(r.Gauss(30,5)); //mean of 30 and sigma of 5
root [3] G10->Draw("same");
There is also
G10->Fill(r.Uniform(20,50)); // Generates a uniform distribution between 20 and 50
G10->Fill(r.Exp(30)); // exponential distribution with a mean of 30
G10->Fill(r.Landau(30,5)); // Landau distribution with a mean of 30 and sigma of 5
G10->Fill(r.BreitWigner(30,5)); mean of 30 and gamma of 5
Final Exam
The Final exam will be to write a report describing the analysis of the data in TF_ErrAna_InClassLab#Lab_16
Grading Scheme:
Grid Search method results
10% Parameter values
20% Parameter errors
30% Probability fit is correct
40% Grammatically correct written explanation of the data analysis with publication quality plots
Report due in my office and source code in my e-mail by Friday, May 8, 2:30 pm (MST)
Report length is between 3 and 15 pages all inclusive. Min Font Size is 12 pt, 1.5 spacing of lines, max margin 2".