Final Lab Frame Moller Electron 4-momentum components in XZ Plane
Jump to navigation
Jump to search
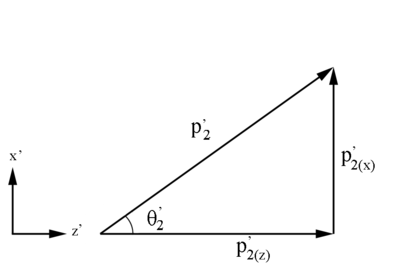
Figure 3: Definition of Moller electron variables in the Lab Frame in the x-z plane.
Using
should always be positive with respect to the total momentum since cosine is an even function.
This is effectively a ratio of momentum in the z direction versus total momentum.
Final Lab Frame Moller Electron 4-momentum components in XZ Plane

Since,
Checking on the sign resulting from the cosine function, we are limited to:
At and all motion is in the z direction.
At The motion is in the x-y plane.