[math]\underline{\textbf{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
Determining Elliptical Equation
As found earlier
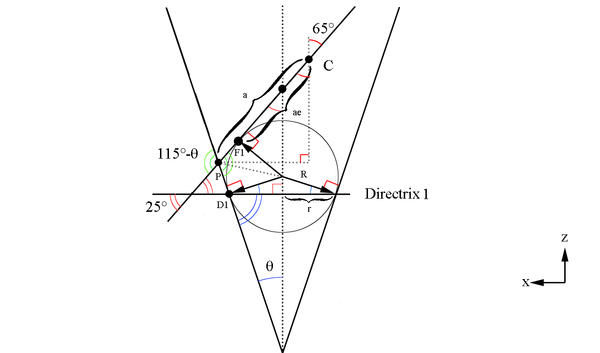
Figure 5: A cone of constant Theta with varying Phi.
[math]CP_x=a\ sin(65^{\circ})[/math]
[math]CP_z=a\ cos(65^{\circ})[/math]
Given the center point coordinates found earlier:
[math]c \equiv (-\Delta x, 0,z+\Delta z)[/math]
[math]c \equiv (-\Delta a\ sin(65^{\circ}), 0,z+\Delta a\ cos(65^{\circ}))[/math]
This gives the location of P([math]\phi=0[/math]) at
[math]P(\phi=0) \equiv (-\Delta a\ sin(65^{\circ})+a\ sin((65^{\circ}), 0,z+\Delta a\ cos(65^{\circ})-a\ cos(65^{\circ}))[/math]
[math]P(\phi=0) \equiv (-\frac{a_2-a_1}{2} sin(65^{\circ})+\frac{a_1+a_2}{2} sin((65^{\circ}), 0,2.53+\frac{a_2-a_1}{2} cos(65^{\circ})-\frac{a_1+a_2}{2} cos(65^{\circ}))[/math]
The height in z can be viewed as a linear function of x and expressed in slope intercept form for a plane:
[math]z_{Plane\ of\ sector}=m_{plane}x+b_{plane}[/math]
where
[math]m_{plane}=\frac{\Delta z}{\Delta x}=\frac{a\ cos(65^{\circ})}{-a\ sin(65^{\circ})}=-cot(65^{\circ})[/math]
[math]b_{plane}\equiv (0,0,2.53)[/math]
The D1 and D2 components can be obtained by finding the x and y components of the two directrix circles, which will be a function of their respective radii and the angle phi around the z axis.
[math]x_{Lower\ Directrix}^2+y_{Lower\ Directrix}^2=r_{Lower\ Directrix}^2\equiv r_{Lower\ Directrix}^2 cos^2(\phi)+r_{Lower\ Directrix}^2 sin^2(\phi)[/math]
Solving for the cartesian components,
[math]x_{Lower\ Directrix}=r_{Lower\ Directrix}\ cos(\phi)\qquad \qquad \qquad y_{Lower\ Directrix}=r_{Lower\ Directrix}\ sin(\phi)[/math]
Similarly,
[math]x_{Upper\ Directrix}=r_{Upper\ Directrix}\ cos(\phi)\qquad \qquad \qquad y_{Upper\ Directrix}=r_{Upper\ Directrix}\ sin(\phi)[/math]
Using the radius information found earlier for the upper and lower Dandelin spheres and directrix,
[math]R_{Lower\ Dandelin}=(ae-\Delta a) tan(65^{\circ})\qquad \qquad \qquad R_{Upper\ Dandelin}=(ae+\Delta a) tan(65^{\circ})[/math]
[math]r_{D1}=R_{Lower\ Dandelin}cos(\theta)=(ae-\Delta a) tan(65^{\circ})sec(\theta)\qquad \qquad\ \qquad r_{D2}=R_{Upper\ Dandelin}cos(\theta)=(ae+\Delta a) tan(65^{\circ})cos(\theta)[/math]
[math]r_{D1}=(\frac{a_1+a_2}{2}\frac{sin(25^{\circ})}{cos(\theta)}-\frac{a_2-a_1}{2}) tan(65^{\circ})cos(\theta)\qquad \qquad \qquad r_{D2}=(\frac{a_1+a_2}{2}\frac{sin(25^{\circ})}{sec(\theta)}+\frac{a_2-a_1}{2}) tan(65^{\circ})cos(\theta)[/math]
The height to the first directrix circle is
[math]z_{D1}=r_{D1}\ cot(\theta)[/math]
The height to the second directrix circle is
[math]z_{D2}=r_{D2}\ cot(\theta)[/math]
This gives the components for a point on the directrix circles as
| [math]x_{D1}=(\frac{a_1+a_2}{2}\frac{sin(25^{\circ})}{cos(\theta)}-\frac{a_2-a_1}{2}) tan(65^{\circ})cos(\theta) cos(\phi)\qquad \qquad y_{D1}=(\frac{a_1+a_2}{2}\frac{sin(25^{\circ})}{cos(\theta)}-\frac{a_2-a_1}{2}) tan(65^{\circ})cos(\theta) sin(\phi)\qquad \qquad z_{D1}=r_{D1}\ cot(\theta)[/math]
|
| [math]x_{D2}=(\frac{a_1+a_2}{2}\frac{sin(25^{\circ})}{cos(\theta)}+\frac{a_2-a_1}{2}) tan(65^{\circ})cos(\theta) cos(\phi)\qquad \qquad y_{D2}=(\frac{a_1+a_2}{2}\frac{sin(25^{\circ})}{cos(\theta)}+\frac{a_2-a_1}{2}) tan(65^{\circ})cos(\theta) sin(\phi)\qquad \qquad z_{D2}=r_{D2}\ cot(\theta)[/math]
|
Using these two points, which will be at the same angle phi around the z axis, a line can be created
[math]\vec d=r_{D2}cos(\phi)-r_{D1}cos(\phi)\ \hat x+r_{D2}sin(\phi)-r_{D1}sin(\phi)\ \hat y+r_{D2}cot(\theta)-r_{D1}cot(\theta)\ \hat z[/math]
Since this line is composed of the difference in the cartesian components of the two points it acts as a direction vector pointing from one point to the next. We can use the fact that a line in space is simply the intersection of two planes which in this situation results in the direction vector. Finding the parametric form equation of this line
[math](x,y,z)=(r_{D1}cos(\phi),\ r_{D1}sin(\phi),\ r_{D1}cot(\theta))+t(r_{D2}cos(\phi)-r_{D1}cos(\phi),\ r_{D2}sin(\phi)-r_{D1}sin(\phi),\ r_{D2}cot(\theta)-r_{D1}cot(\theta))[/math]
Solving for the individual cartesian components
[math]x=r_{D1}cos(\phi)+t(r_{D2}cos(\phi)-r_{D1}cos(\phi))\qquad \qquad y=r_{D1}sin(\phi)+t(r_{D2}sin(\phi)-r_{D1}sin(\phi))\qquad \qquad z=r_{D1}cot(\theta)+t(r_{D2}cot(\theta)-r_{D1}cot(\theta))[/math]
[math]\Rightarrow t=\frac{x-r_{D1}cos(\phi)}{r_{D2}cos(\phi)-r_{D1}cos(\phi)}=\frac{y-r_{D1}sin(\phi)}{r_{D2}sin(\phi)-r_{D1}sin(\phi)}=\frac{z-r_{D1}cot(\theta)}{r_{D2}cot(\theta)-r_{D1}cot(\theta)}[/math]
Since this condition implies that the 3 equations listed above for all conditions, we can solve for the [math]\phi=0[/math] situation which must then hold for all other instances of [math]\phi[/math]
[math]\frac{x-r_{D1}cos(\phi)}{r_{D2}cos(\phi)-r_{D1}cos(\phi)}=\frac{z-r_{D1}cot(\theta)}{r_{D2}cot(\theta)-r_{D1}cot(\theta)}[/math]
[math]\frac{x-r_{D1}cos(\phi)}{(r_{D2}-r_{D1})cos(\phi)}=\frac{z-r_{D1}cot(\theta)}{(r_{D2}-r_{D1})cot(\theta)}[/math]
[math]\frac{(x-r_{D1}cos(\phi))(r_{D2}-r_{D1})cot(\theta)}{(r_{D2}-r_{D1})cos(\phi)}+r_{D1}cot(\theta)=z[/math]
Using the condition that on the plane
[math]z_{plane}=-cot(65^{\circ})x+2.53[/math]
We can substitute for z to find the point of intersection for the plane and cone at a given [math]\theta[/math] and [math]\phi[/math]
[math]\frac{ \left( x_P-r_{D1}cos(\phi) \right) cot(\theta)}{cos(\phi)}+r_{D1}cot(\theta)=-cot(65^{\circ})x_P+2.53[/math]
[math] \left ( \frac{x_P}{cos(\phi)}+r_{D1}-r_{D1} \right )cot(\theta )=-cot(65^{\circ})x_P+2.53[/math]
[math] \left ( \frac{x_P}{cos(\phi)} \right )cot(\theta )+cot(65^{\circ})x_P=2.53[/math]
[math] \frac{x_P\ cot(\theta )}{cos(\phi)}+cot(65^{\circ})x_P=2.53[/math]
[math] x_P \left (\frac{ cot(\theta)+cos(\phi)cot(65^{\circ})}{cos(\phi)}\right )=2.53[/math]
[math]x_P(cot(\theta)+cos(\phi)cot(65^{\circ})=2.53cos(\phi)[/math]
| [math]x_P=\frac{2.53cos(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
|
[math]\Rightarrow t=\frac{x-r_{D1}cos(\phi)}{r_{D2}cos(\phi)-r_{D1}cos(\phi)}=\frac{y-r_{D1}sin(\phi)}{r_{D2}sin(\phi)-r_{D1}sin(\phi)}=\frac{z-r_{D1}cot(\theta)}{r_{D2}cot(\theta)-r_{D1}cot(\theta)}[/math]
[math]\frac{x_P-r_{D1}cos(\phi)}{r_{D2}cos(\phi)-r_{D1}cos(\phi)}=\frac{y-r_{D1}sin(\phi)}{r_{D2}sin(\phi)-r_{D1}sin(\phi)}[/math]
[math](r_{D2}sin(\phi)-r_{D1}sin(\phi))\frac{(x_P-r_{D1}cos(\phi))}{r_{D2}cos(\phi)-r_{D1}cos(\phi)}=y_P-r_{D1}sin(\phi)[/math]
[math](r_{D2}-r_{D1})sin(\phi)\frac{(x_P-r_{D1}cos(\phi))}{(r_{D2}-r_{D1})cos(\phi)}=y_P-r_{D1}sin(\phi)[/math]
[math]sin(\phi)\frac{(x_P-r_{D1}cos(\phi))}{cos(\phi)}=y_P-r_{D1}sin(\phi)[/math]
[math]y_P=sin(\phi)\frac{(x_P-r_{D1}cos(\phi))}{cos(\phi)}+r_{D1}sin(\phi)[/math]
[math]y_P=tan(\phi)x_P-r_{D1}sin(\phi)+r_{D1}sin(\phi)[/math]
[math]y_P=tan(\phi)x_P-r_{D1}sin(\phi)+r_{D1}sin(\phi)[/math]
[math]y_P=tan(\phi)\left (\frac{2.53cos(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}\right )[/math]
| [math]y_P=\frac{2.53sin(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
|
[math]z_P=\frac{(x_P-r_{D1}cos(\phi))(r_{D2}-r_{D1})cot(\theta)}{(r_{D2}-r_{D1})cos(\phi)}+r_{D1}cot(\theta)[/math]
[math]z_P=\frac{(x_P)cot(\theta)}{cos(\phi)}[/math]
[math]z_P=\frac{(\frac{2.53cos(\phi)}{(cot(\theta)+cos(\phi)cot(65^{\circ})})cot(\theta)}{cos(\phi)}[/math]
| [math]z_P=\frac{2.53cot(\theta)}{(cot(\theta)+cos(\phi)cot(65^{\circ})}[/math]
|
[math]\underline{\textbf{Navigation}}[/math]
[math]\vartriangleleft [/math]
[math]\triangle [/math]
[math]\vartriangleright [/math]
