Conic Sections
Jump to navigation
Jump to search
Conic Sections
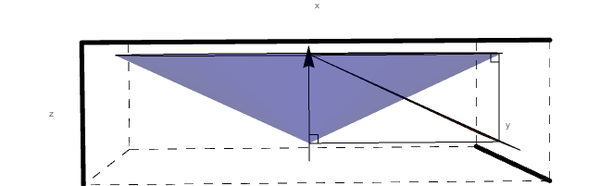
Looking just at sector 1, we can see that the intersection of level 1 and the cone of constant angle theta forms a conic section.
Show[sector1,PhiCone,BeamLine,Bisector0Sector1,Bisector0perpSector1,Bisector0Cone,Bisector0perpCone,RightAngleVertical,RightAngleHorizontal,RightAngleVertical2,RightAngleHorizontal2]
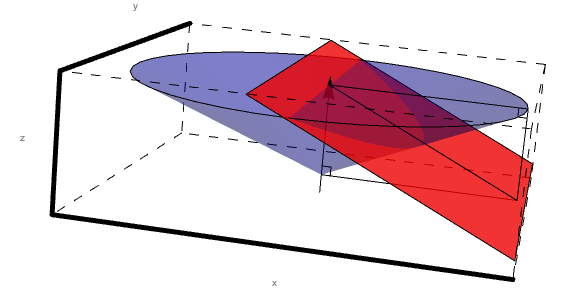
Without loss of generalization, we can extend the triangle to an infinite plane to aid in viewing the conic section. Again, this falls outside of the experimental design range, but simulations would not occur in this forbidden zone.
sector1plane =
Graphics3D[{Red, Opacity[.8],
InfinitePlane[{{0, 0, 2.53}, {3.13 \[Sqrt]3, .617,
0}, {3.13 \[Sqrt]3, -3.13, 0}}]},
BoxStyle -> Dashing[{0.02, 0.02}], Axes -> True,
AxesLabel -> {"x", "y", "z"}, Ticks -> None,
AxesStyle -> Thickness[0.01]];
Show[sector1plane, PhiCone, BeamLine, Bisector0Sector1, \
Bisector0perpSector1, Bisector0Cone, Bisector0perpCone, \
RightAngleVertical, RightAngleHorizontal, RightAngleVertical2, \
RightAngleHorizontal2]
Following the rules of conic sections we know that the eccentricity of the conic is given by:
where β is the angle between the plane and the horizontal and α is the angle between the cone's base and the horizontal.
Examining the different conic sections possible we know that: