Alpha particle simulation related
Source Activity Calculations
U-233 thin layer exists on the cathode of GEM detector, the thickness of the circular layer estimated between 0.04-0.08 mm with 2.5 cm diameter. On July 12, 2013, measurements was performed to estimate the rate of alpha and beta particles that are emitted from the source as shown in the following table.
| Shutter position | Alpha particles /min. | Beta particles /min. |
| Open | 6879 | 900 |
| Close | 1 | 38 |
Energy threshold for electron and gamma entering detector
Detemine the energy threshold that an electron and a photon need to surpass in order to pass through the kapton, gas, the copper cathode, and the FR4.
Draw a picture with dimensions of all the layers
Energy -vs- counts per incident particle
Photon and electron Energy -vs- distance through the detector
energy straggling plot at the point where particle just makes it through the detector
Alpha Particles ionization simulation using GEANT4
GEANT4 simulates the ionization of alpha particles in Ar/CO2 90/10 gas. Geant4 can simulate the ionization process for alpha particles. Unfortunately the value of the step function underestimates the number of delta electrons even after decreasing the step cut to 1 nm. Also,using GEANT4 overestimates the range of alpha particles in Ar/CO2 gas when compared to those that srim calculates File:Alpha range ArCo2.txt, the following table shows the maximum range of alpha particles that are emitted from the U-233, and the ranges calculated by srim.
| Alpha Energy (MeV) | G4 Range (cm) | Srim Range (um) |
| 1.0 | 0.56599 | 129.49 |
| 2.0 | 1.1467 | 255.91 |
| 3.0 | 1.9024 | 417.27 |
| 4.0 | 2.8012 | 612.45 |
| 5.0 | 3.8425 | 839.91 |
Based on the previous table, GEANT4 failed to calculate the expected alpha range for most alpha energies, and underestimated the number of alpha's delta electrons emitted through that range, but it is still useful tool to simulate the primary delta electrons when negative beta particles pass through a defined medium.
Alpha propagation through the drift area with 600V drift voltage
U-233 is an alpha-emitter source, alpha particles at least 4.85 MeV as kinetic energy when they leave the nucleus. The voltage needed to stop an alpha of an energy of 4.85 MeV can be calculated as the following:
where V is the applied voltage.
for an alpha K.E = 4.85 MeV , q = 2e, so:
Compared to the drift voltage, the drift voltage effect is negligible, since the magnitude of work applied against each alpha is just 1.2 keV as shown below:
Alpha's Ionization and Electron Rate Using G4
Simulted Range by srim and trim and G4
the range of alpha particles simulation was performed using Srim and Trim and G, the following table shows the results
| Alpha Energy (MeV) | medium | measured range | G4 Range | Srim Range (um) |
| 5.46 | CO2 | 4.54 | 4.04 +_0.09 | 5.01 +_ 0.09 g/cm^2 |
| 8.75 | Ar | 8.09 | 7.99+_ 0.11 | 3.94 +_0.05 |
As result simulating alpha ionization using G4 is more accurate than using srim and trim for any argon gas mixture.
What is the charge in the ADC and how often do you see it
The simulation for the range of alpha particles was performed using Srim and Trim and GEAT4 as shown in the figure above. GEANT4 simulation for alpha range is almost the same as those for the measured range by Hanke (1971), who measured alpha particles range in a pure argon. another package is used to simulate the range, unfortunately srim and trim does not simulate the range of alpha particles when it is lower than 5.33 MeV, so we only have one value for the alpha range simulation in CO2 gas.
File:Excitation ionization ratio saito 2003.pdf
Geant4 is used to estimate the number of electrons that are emitted in the drift region after in presence the FR4 shutter. Simulating alpha's ionization output in the drift region was divided in three stages:
- Alpha interaction with an FR4 shutter in vacuum.
- Alpha interaction with an Ar/CO2 gas.
- Alpha interaction with the FR4 shutter and the Ar/CO2 gas.
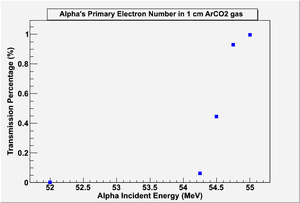
The first stage describes the alpha particles when they stopped by the FR4 shutter of thickness of 1 mm, the following figure shows the percentage of the number of alphas that penetrate the shutter, it shows for a complete penetration, alpha's energy has to be around 60 MeV. It is Previously mentioned that the emitted alpha particles from U-233 has a maximum energy of 8.4 MeV, So the shutter is able to stop all the emitted alpha particles.
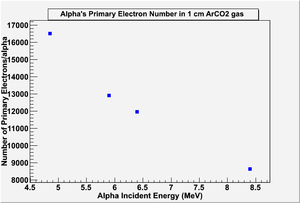
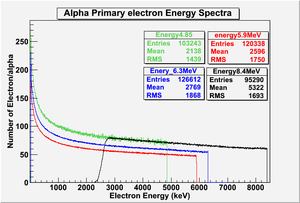
As the shutter is open, the alpha particles travel through the drift region, a 1 cm deep of Ar/CO2 gas, primary electrons appear as a result of alpha collision with Ar-atoms which described in G4 as (hIoni) ionization. The number of primary electrons of each alpha particle is depend on its energy. the plot below shows the emitted alpha's primary electrons number in Ar/CO2 gas:
It is noticed that geant4 simulation for alpha's range in ArCO2 gas exceeds the depth of the drift region. So a decrease in the number of primary electrons as alpha's energy increases. GEANT4 alpha's range meets with STAR database on NIST website. (STAR calculated range is 7.4 cm for 8 MeV alpha particle passing through Ar-gas).
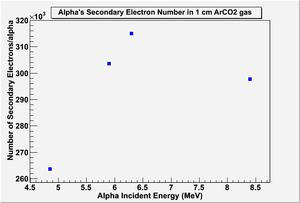
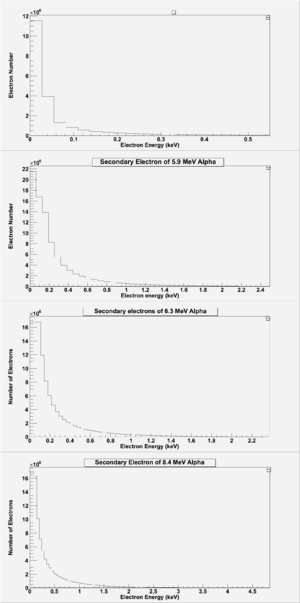
Looking at the number of secondary electrons, the figure shows that the number of secondary electrons that are collected in the drift region; the number of primary electrons is almost the same for all alpha's energies that are emitted from U-233. keeping in mind the plot for primary electrons; the number of secondaries increases by increasing alpha's energy, i.e the kinetic energy of the primary electrons in case of 8.4 MeV alphas is more than those for 4.85 MeV alphas that made number of secondary electrons for all alpha's energy is almost the same. So the final rates for all alpha particles in the energy range of 4.85 MeV to 8.4 MeV is almost the same, since the number of secondary electrons is almost the same which is in average 300k electron/alpha assuming the same emission percentage for all alpha's energies.
The spectrum for 8.4 MeV is different since GEANT4 has an arbitrary maximum kinetic energy for using bethe-block formula in the energy loss model, so as the energy is higher than 8 MeV, another equation is used with different parameters, and has a higher minimum energy for the electron tracking.
Geant4 doesn't use direct ionization cross section database reference to simulate the ionization process, but geant4 considers the ionization as a combination of number of physical processes as mentioned in the link. [1]
Calculating the number of the delta electrons without using GEANT4
There is another way to calculate the number of delta electrons without using GEANT4. It starts by calculating the average energy loss by the alpha particles and the average energy loss per unit length in Ar/CO2 gas using the Bethe-Block equation. It then uses the the following equation:
to calculate the actual energy loss by ionization , where represents random landau number.
By dividing the energy loss by the minimum energy for producing a pair of ion-electron pair W, this equation yields the number of electrons emitted by ionization.
Srim can simulate the motion of an alpha particle in Ar/CO2 gas by allowing for the change in the stopping power per unit length. It can also show the ionization energy loss as shown in the following figure:
This figure shows the ionization energy loss of 1000 alpha particles as they pass through Ar/CO2 gas of a 1 cm length.
To calculate the ionization for each ion-electron pair in 90/10 Ar/CO2 gas:
where s and p are the stopping power and the partial pressure for each gas.
| Alpha Energy (MeV) | Stopping power in Ar (MeV cm2/g) | Stopping power in CO2 (MeV cm2/g) | Stopping power in Ar (eV/Angstrom) | Stopping power in CO2 (eV/Angstrom) |
| 4.8 | 4.159E+02 | 6.822E+02 | 0.006912258 | 0.0124242264 |
| 5.9 | 4.695E+02 | 7.128E+02 | 0.00780309 | 0.0129815136 |
| 6.3 | 4.846E+02 | 7.704E+02 | 0.008054052 | 0.0140305248 |
| 8.4 | 5.671E+02 | 8.744E+02 | 0.009425202 | 0.0159245728 |
The partial pressures for 90/10 Ar/CO2 gas mixture that runs under atmospheric pressure (1026 Pa) and room temperature and density of 1.66201E-03 g/cm3
| Partial Pressure (pa) | (eV) | |
| Ar | 25 | |
| CO2 | 34 |
The following spreedsheet shows the calculations for the expected number of electrons. File:Stoppingpower trim calculations.xls
Number of Primary ionization events per cm
- Inside the chamber
The figures show the threshold energy for photons traveling in the detector and the number of the absorbed photons within the detector's drift area. Photons travel through the drift area and primarily interact by photoelectric effect with the gas's atoms and molecules; a photon's energy may increase up to 1.1 MeV and still the most probable interaction with the medium is the photoelectric effect. Figure xx1 shows the same numbers of primary electrons produced by an incident photon simulation by GEANT4; once when all photon's interactions are considered (red), and once when only the photoelectric effect only considered (blue). It also shows that all the photons are absorbed by Ar/CO2 gaseous medium. Since the incident photon energy varies from 10 keV up to 1.1 MeV, only the absorbed photons within a 1 cm will affect the detector signal. GEANT4 simulation shows that the dominant interaction is the photoelectric effect even if the incident photon energy reaches 1.1 MeV, and that 25 percent of the photons will be absorbed when their energy is 25 keV, as the energy increases the number of photons decreases to reach 0.03 when the photon energy is 96.1 keV. As a result, gamma energy, emitted by U-233 or bremsstrahlung radiation that appears when the lineac is in operation, should have a maximum energy of 96.1 keV as it is in the detector's drift area, which maximizes the effect on the detector's signal.
- 7cm Outside the chamber
Photons may reach the detector's drift area and affect its signal when they pass through the kapton window or (less probably) through the ertalyte plastic. Normally, the detector structure is built from materials that prevent the photons of specific energies from causing ionization in the drift area. Figure xx3 shows the incident photon energy at a 7 cm distance from the kapton window and the number of photons absorbed in the drift area that cause ionization by photoelectric effect.
The figure shows a maximum number of absorbed photons; when the incident photon energy is 60 keV, 46 percent of the photons get absorbed by the drift region.
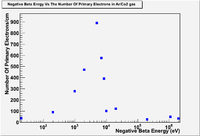
from beta particle as a function of beta particle energy using Garfield and GEANT4
GEANT4 can simulate the primary number of delta electrons for a negative beta particle penetrating ArCO2. Using the TestEm10 example and choosing the appropriate default cut, GEANT4 counts the same number of primary delta electrons for negative beta particles with 1.1 MeV energy, and determines the energy and the momentum of the delta electrons depending on Moller or Bhabha's scattering, and depending on the value of the kinetic energy cut used.<ref name = "Urban">Urbán, L. (1998, 10 09). Geant4 physics reference manual. Retrieved from http: //geant4.web.cern.ch/geant4/G4UsersDocuments/UsersGuides/PhysicsReferenceManual/html/node41.html </ref>
The following figure shows Garfield simulation for the number of electrons that are collected in the drift region when the shutter is open and as the electron passes a 90/10 Ar/CO2 gas:
Overlay with dE/dx formula and fill in gaps
something is wrong with G4 result for electron energies below 1 keV.
from photon as a function of photon particle energy using Garfield and GEANT4
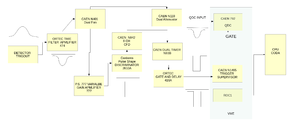
Chamber Geometry in GEANT4
The chamber geometry for the GEM chamber is set for Calculating the created charge in the detector's drift area is shown below:
Charge particles and photons primary ionization
The physical interactions that take place inside the detector are simulated by GEANT4.9.6 to estimate the primary charge collected by the drift electric field in GEM detector. GEM detector depends mainly on the particles’ interaction with Ar/CO2 atoms and molecules, especially those that directly (or indirectly) produce free charge that can be collected by the drift electric field. Specifically in the GEM detector described by section XX, the detector signal can be produced by gamma rays, electrons, or neutrons. GEANT4.9.6 has been used to estimate the primary charge caused by those particles in case of electrons and neutrons, but for photons, GENAT4 is used to produce the photoionization energy spectrum for Ar/CO2 gas.
The simulation started by determining the number of primary electrons produced by charged particles in Ar/CO2. The number of primary electrons depends on the particles’ charge and mass and kinetic energy. As a result, alpha particles have the highest number of primary electrons, electrons have less primary electrons, and photons have the least number of primary electrons produced per photon, assuming that photoabsorption is the dominant process in Ar/CO2 gas for an energy range of 1 to 300eV.
By modifying EmTest10 example in GEANT4.9.6, the number of primary electrons produced by an electron travels 1 cm is shown in the figure below:
The figure also shows Garfield simulation for an electron's primary ionization; it is noticed that the GEANT4.9.6 results match those of Garfield when the minimum incident electron energy is eV. Such an energy value is much lower than the threshold kinetic energy which an electron needs to make ionizations in the detector's drift region, since the threshold kinetic energy for an electron is more than 2 MeV 5cm away from the detector's window.
GEANT4.9.6 predicts the number of the primary electrons for a photon. Photon ionization has the least number of electrons, even producing an free electron is constrained to the electronic structure of Ar/CO2 gas.
GENAT4.9.6 does not predict the Argon photoabsorption spectrum specifically for each energy as shown above, the photon energy may have eV shift. It is worth to mention if the photon is not in the drift region, then the detector is completely blind for any photon of energy of 20-300 eV (their range in fm). In case of a 50 keV photon or more, the photon will easily pass the detector chamber without affecting its medium if only photoionization is considered, within that energy range Compton scattering cross section increases, it will produce an electron and a photon in the drift region that can easily be detected. Being in am accelerator environment, photon interaction becomes dominant by Compton Scattering interaction in a way that makes the detector in efficient to detect any other particle.
File:Excitation ionization ratio saito 2003.pdf
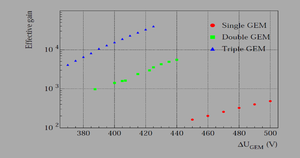
Garfield simulated the gain when the voltage for each GEM detector is 466V in average, the gain is 1.1617 x 10^4 +_1099 for 293k and 1021 Pa.
In our case, by the end of the drift area, the electron will have 3 stages of multiplication by GEM preamplifiers, the voltage on the potential divider circuit is 2800 kV, which will provide 300-350 V on each GEM preamplifier. Garfield succeeded to simulate the gain for 2.8 kV triple GEM in Ar/CO2 90/10 gas mixture under STP conditions of an average value of 7.88 +_ 2.8 x 10^3. So, the charge collected by the charge collector for 4.82 MeV alpha particles is expected to be:
The figure below shows the signal processing electronics configuration,
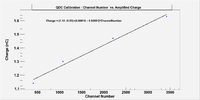
A signal of an amplitude 11.8 mV passed through the loop to output a 20.8 mV amplitude signal as shown by a 50 ohm terminated oscilloscope, using the figure below, the amount charge that ADC collected is,
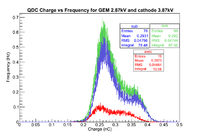
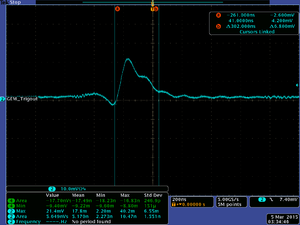
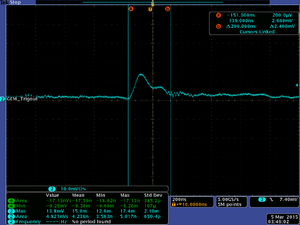
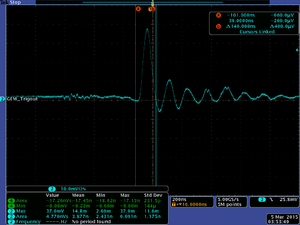
03/05/15 Measuring the GEM charge from the oscilloscope
A 50 ohm terminated oscilloscope measured the pulse that comes directly from the tripe GEM trigout as the voltage 2.8, 3.8 kV for the triple GEM and the cathode successively, the triangle pulse amplitude is 19 mV, and it width is 299 ns, if the pulse represents an alpha ionization, then the number of alphas considering the charge received directly from the trigout is,
Also the number of alphas for the second figure is 1.6, and for the third one is 2.1.
Total charge on anode
Now use the primary above and include detector gain to calculate total charge hitting the anode and getting readout.
<References/>
GO BACK [2]