A W thesis
Abstract
This thesis reports on a measurement of the detection limit improvement of coincidence photon activation analysis over the more common Photon Activation Analysis (PAA) for Yttrium (Y-89). PAA is a multi-elemental analysis method capable of quantifying the nuclear isotopes present in materials by activating isotopes of interest and measuring the energy of photons released when the nucleus de-excites. If the isotope of interest de-excites by emitting a cascade of multiple photons, then coincidence photon activation analysis may be used to detect photons that are emitted in coincidence. A foil of natural Yttrium was irradiated at the Idaho Accelerator Center (IAC) using the bremsstrahlung photons produced when a 22 MeV electron beam impinged a 0.3" Tungsten target. A coincidence measurement was performed on the activated Yttrium using a HPGe and NaI detector. The measurement found that for every $10^{12}$ atoms of Y-89, one atom of Y-88 was produced. Coincidence photon activation was able to measure a minimum of $5\times 10^{18}$ atoms of Y-89 in the 0.03 g foil improving the detection limit by at least a factor of two over standard PAA.
Key Words: Photon Activation Analysis (PAA), coincidence, Yttrium, detection limit
Y-88 source #130113-004
Foil weight: 0.0288 +/- 0.0002 g
Foil Size: W=1/2 inch, H=3/4 inch
Foil Area: 3/8 in^2 (2.42 cm^2)
Here we have: P = E I
Here, [P] Watts, [E] MeV, and [I] A
- Accelerator Settings
| beam energy | 22 MeV |
| Rep Rate: | 170 Hz |
| I_peak: | 80 mA/pulse |
| pulse width: | 4 s |
Time on for one second is 1 us. and Time off is 0.999999 s The average current 0.999999 * 0 + 0.000004*170*80mA = 54.4 A.
P = (22 MeV) (54.4 A) = 1.2 k Watt.
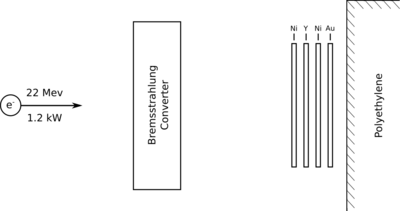
Three 0.100" W disks separated by about 0.150" of water.
Introduction
Photon Activation Analysis (PAA) is a multi-elemental analysis method that performs photon spectroscopy on materials activated by high energy (MeV) photons to measure the concentrations of elements in a material. The method measures the energy of photons emitted by decaying nuclei using a high purity Germanium detector that has a typical photon energy resolution of 1 keV. Although the observed photon energy may be used to construct a finite list of decaying nuclei candidates, the specific decaying nuclear isotope emitting the photon is usually uniquely identified once a half-life is measured. PAA is able to identify the presence of several nuclei by detecting photons emitted by decaying nuclei.
Many activated nuclei de-excite to the ground state by transitioning through several intermediate states and in the process emitting photons within a picosecond or less timescale of each other. This cascade of gamma rays may be used to improve the identification of the decaying nucleus used in traditional PAA. Requiring the detection of two $\gamma$'s, a method that will be referred to as Coincidence Photon Activation Analysis (CPAA), should reduce the background found in traditional PAA. This thesis quantifies the improvement achieved by CPAA in terms of the lowest number of activated nuclei, the detection limit, that PAA and CPAA can measure.
In addition to PAA, there are several other analytical techniques used to quantify the elemental composition of materials. They each have their own associated advantages and disadvantages. For example, AAS and ICP methods chemically process a sample, usually by removing a portion of the material and destroying the sample. This is not an ideal technique when investigating materials such as artifacts and antiques, where cutting away pieces for a sample is not desireable. Additionally, there is a danger of introducing contamination during preparation procedures. However, unlike some techniques that are limited to surface studies, these two methods can be used for volume or bulk analysis. Further explanations on some of the more readily available techniques and their differences may be found in Appendix A.
The focus of this thesis is on the detection limits of PAA and CPAA. For comparison, Table 1.1 lists several existing elemental analysis methods along with current detection limits. The detection limits range from 0.1 to 100 parts-per-million (ppm or ). While the particular focus is on improving PAA's detection limit, the coincidence method can easily be used on a complimentary nuclear method, Neutron Activation Analysis (NAA). The physics of nuclear activation is described below.
table of detection limits -vs- Method
| Method | Detection Limit (ppm) |
| ICP-MS | |
| ICP-AES | |
| AAS | 1-100 |
| PIXE | 0.5-5 |
| XRF | 3-20 |
| NAA | 0.01-10 |
| PAA | 0.01-100 |
Nuclear Activation Methods
Nuclei of stable elements can become radioactive when they undergo an inelastic collision that results in the addition or removal of a nucleon or several nucleons from the nucleus. Nuclei are usually left in an unstable state and will almost instantaneously de-excite into a more stable configuration. This process involves the prompt emission of particles or photons. If the initial nucleus to be activated is denoted by $$, the incident radiation particle as $a$, and the product nuclide and promptly emitted particles are denoted by $$ and $b$ respectively, the reaction can be represented by the equation
or, in the abbreviated form
The type of the nuclear reaction depends upon the target nucleus and the nature and energy of the incident radiation. Many of these product radioactive nuclei decay through $\beta$ and subsequent $\gamma$ emission. The $\gamma$-rays are characteristic of that particular decay process. By precise determination of the $\gamma$-ray energies, it is usually possible to determine not only which isotopes are present, but from the $\gamma$ intensities it can be determined exactly how much of the original target nucleus was present and consequently the amount of that element present in the sample. The use of neutrons and photons as the activating radiation particle are described below.
Neutron Activation Analysis (NAA)
Neutron activation analysis (NAA) is a non-destructive technique, similar to PAA, used to measure trace elements in materials to within detection limits of 0.01 $\rightarrow$ 10 ppm~\cite{Pollard}. In NAA, the incident radiation particle is a neutron. Several different neutron sources are available, but only a few that offer the high neutron fluxes useful for NAA. These include reactors and accelerators. Since they have high fluxes ($10^{13} \frac{n}{cm^2 \cdot s}$) of neutrons from uranium fission, nuclear reactors offer the highest available fluxes~\cite{Glascock}. The sequence of events taking place during the most common type of nuclear reaction for NAA, namely neutron capture (n,$\gamma$), is illustrated in Figure~\ref{fig:Neutron_Capture}.
Upon irradiation, a neutron is absorbed by the target nucleus. The compound nucleus transitions to an excited and unstable state. This unstable nucleus de-excites into a more stable configuration by emitting one or more prompt gamma rays. In most cases, this new configuration tends to be a longer lived radioactive nucleus. The newly formed radioactive nucleus now decays by the emission of one or more characteristic delayed gamma rays. The half-life of this decay is unique to the radioactive nucleus. An NAA measurement, in principle, falls into two categories: (1) prompt gamma-ray neutron activation analysis (PGNAA), where measurements are taken during the irradiation of a sample, or (2) the more common delayed gamma-ray neutron activation analysis (DGNAA), where measurements follow radioactive decay. There are several types of detectors employed in NAA. Most are designed to detect the emitted γ radiation. The detectors most commonly used are scintillation type, with radiation sensitive crystals such as thallium-doped sodium iodide (NaI(Tl)), or semiconductor type detectors. Hyper-pure or intrinsic germanium (HPGe) detectors are the semiconductor type most commonly operated for NAA.
Photon Activation Analysis (PAA)
In photon activation analysis (PAA)~\cite{Segebade}, nuclei in the sample material are excited into radioactive meta-stable states through exposure to high-energy (MeV) photons. PAA has detection limits of 0.01$\rightarrow$100 ppm~\cite{Segebade}~\cite{Lutz}. The photon source is typically produced by accelerating electrons onto a target layer of metal with a high atomic number, such as Tungsten. The de-acceleration of electrons passing through the target (radiator) produces electromagnetic radiation. Such radiation is referred to as bremsstrahlung radiation. If the bremsstrahlung radiation strikes a sample nucleus and results in the removal of a nucleon from the nucleus, the nucleus will more often than not be left in an excited state. The resulting nucleus is usually unstable and de-excites by emitting beta or gammas. The energy of the emitted $\gamma$ radiation is usually characteristic of the nuclide. A measurement of the gamma energy can thus be used to identify the nuclear isotope. Similar to NAA, gamma radiation is commonly measured with radiation sensitive crystals, such as thallium-doped sodium iodide (NaI(Tl)), or semiconductor type, such as HPGe detectors. For coincidence photon activation analysis, two detectors are used to require the detection of two photons decaying in coincidence.
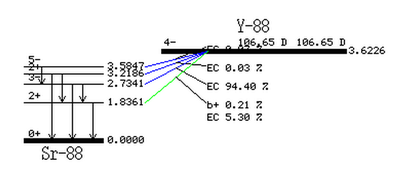
When performing nuclear activation on a sample, all nuclei are affected. Contaminates present in a sample will also be activated and contribute to the signal background. It was desirable to activate an isotope with half-lives of days to reduce this background and study the impact of CPAA. Photon activated materials with such long half-lives allow a waiting period for the short lived contaminates to decay away and still have a signal that could be measured. It would also allow multiple measurements and systematic studies could be performed. Of the materials available, Yttrium met this requirement. The half-life of activated Yttrium (Y-88) is 106.63 days. Details of Yttrium activation and decay process are described below.
File:Photon Activation Analysis 1971 Lutz.pdf
Y-89 Activation
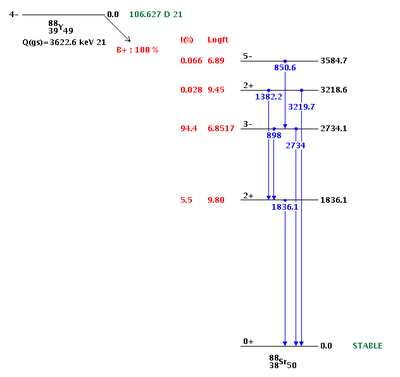
The only natural occurring isotope of Yttrium is Y-89. During photon activation of a Yttrium foil, a neutron is removed from the nucleus in a reaction denoted as . The resulting Y-88 nucleus is radioactive with a half-life of 106.63 days. Table~\ref{tab:photon_lines} gives the prominent photon energies emitted by an excited Y-88 nucleus. The 898 keV and 1836.1 keV lines have been observed to be the most prevalent with relative intensities of 93.7$\%$ and 99.2$\%$.
Table~\ref{tab:coincidence_gamma} provides a list of Y-88 photons along with the gammas they are in coincidence with. Note that the 898 keV and 1836.1 keV lines are also in coincidence. This coincidence occurs when the 2734.1 keV state, with a 94$\%$ branching ratio, makes a transition after 0.7 ps to the 1836.1 keV state, emitting a 898 keV photon. The 1836.1 keV state will decay to the ground state after 0.154 ps and emit a 1836.1 keV photon. A diagram of the photon energies and their transitions can be seen in Figure~\ref{fig:Y-88_decay}. The total lifetime of the transitions is less than a picosecond~\cite{times}. For our experimental setup, discussed in section~\ref{Discrimination}, the coincidence timing window was set to 200 ns, so for effective purposes the 898 keV and 1836.1 keV photons are considered in coincidence and will be used for our PAA analysis.
PAA utilizes photon spectroscopy to measure the concentration of elements in a material. It is predicted that by requiring the detection of two photons in coincidence, CPAA will allow the signal background to be decreased and measure a lower detection limit. The primary objective of this thesis will be to quantify the improvement of CPAA in the detection limit using the activation of Y-89. A determination of the detection limit for PAA and CPAA was made using the apparatus described in the following chapter.
Y-88:
http://physics.nist.gov/cgi-bin/Xcom/xcom3_1-t
http://atom.kaeri.re.kr/cgi-bin/decay?Y-88%20EC
https://www-nds.iaea.org/relnsd/vcharthtml/VChartHTML.html
| Energy (keV) | Relative Intensity |
| 850.6 | 0.065 |
| 898.042 | 93.7 |
| 1382.2 | 0.021 |
| 1836.063 | 99.2 |
| 2734.0 | 0.71 |
| 3219.7 | 0.0070 |
| Energy (keV) | Coincidence gamma |
| 850.6 | 898.042, 1836.063, 2734.0 |
| 898.042 | 850.6, 1836.063 |
| 1382.2 | 1836.063 |
| 1836.063 | 850.6, 898.042, 1382.2 |
| 2734.0 | 850.6 |
| 3219.7 |
http://www.nndc.bnl.gov/chart/decaysearchdirect.jsp?nuc=88Y&unc=nds
| Energy (keV) | Decay Time (ps) |
| 898.042 | 0.70 |
| 1836.063 | 0.154 |
http://www.nndc.bnl.gov/chart/getdataset.jsp?nucleus=88SR&unc=nds
Concerning the choice of sample that would be activated for PAA study, the main criteria for the activating material was it should allow the testing of coincidence with a high energy and a low energy gamma line. A typical energy spectrum can suffer signal lose in the lower energy ranges do to noise. If a system can trigger on a high energy line in the coincidence measurement, the low energy line can be pulled out of the background noise. From the resources conveniently available, yttrium meet the high and low energy line requirements, and had some additional characteristics that were favorable for testing. That half-life of activated yttrium is 106.63 days. This longer decay time provided a method for decreasing the noise of background decay after irradiation. It is uncertain how long it takes for background to decay after activation. An photon activated material with a long half-life allowed a waiting period for the short lived contaminates to decay away and still have a signal that could be measured. Details of yttrium activation and decay process are described below.
The only natural occurring isotope of yttrium is Y-89. During photon activation of a yttrium foil, a neutron is removed from the nucleus in a reaction. The resulting Y-88 is radioactive with a half-life of 106.6 days. TableXX.YY gives the photon lines for a Y-88 sample. The 898 keV and 1836.1 keV lines have been observed to be the most prevalent with relative intensities of 93.7% and 99.2%. TableXX.YY provides a list of Y-88 photons with the gammas they are in coincidence with. Note that the 898 keV and 1836.1 keV lines are also in coincidence. This coincidence occurs when the 2734.1 keV state, which occurs 94% of the time, makes a transition after 0.7 ps to the 1836.1 keV state, emitting a 898 keV photon. The 1836.1 keV state will decay to the ground state after 0.154 ps and emit a 1836.1 keV photon. A diagram of the photon energies and their transitions can be seen in figureXX.YY. The total lifetime of the transitions is less than a picosecond. For our experimental setup, discussed in sectionXX.YY, the coincidence timing window was set to 200 ns, so for effective purposes the 898 keV and 1836.1 keV photons are considered in coincidence and will be used for our PAA analysis.
Y-89:
Binding Energy: 775538.048 +- 2.349 keV
http://www.tandfonline.com/doi/pdf/10.1080/18811248.2010.9720959
File:Y-89 N-knockout-Xsect JNS 2010 Kalam.pdf
Apparatus
Photon activation analysis (PAA) of a Yttrium sample requires the use of an electron accelerator to produce the MeV energy photons used to irradiate the sample and a system of detector to measure the photon's emitted by the post-irradiated sample. Idaho State University's Idaho Accelerator Center (IAC) was used to irradiate the Yttrium sample and perform photon spectroscopy measurements. The IAC's 48 MeV electron linear accelerator (LINAC), commonly referred to as "Jack", was used to accelerate electrons to an energy of 22 meV. An average electron beam current of 54.4 \muA impinged a bremsstrahlung target composed of three 0.100" thick Tungsten disks as illustrated in Figure 2.1. The three Tungsten disks were separate by 0.150" to allow water based cooling of the 1.2 kW deposited on the disks by the incident electron beam. A set of target foils were placed 1 m downstream of the Tungsten target to be irradiated by the Bremsstrahlung photons. The Yttrium fool was placed between two nickel foils and attached to a polyethylene block. An additional gold foil was inserted between the nickel foil and polyethylene. Table YYY describes the dimensions of the foils used.
Coincidence counting Apparatus
Data Analysis
Introduction
After acquiring the material spectrum using the set-up described in the previous chapter, the 898 keV and 1836.1 keV energy lines are analyzed in order to calculate the using photon activation analysis.
It is important to review some terminology use before proceeding with the analysis process. As shown in chapter 2, the module set up included a CAEN 3 Fold Logic Unit. This unit allowed runs to be conducted with an OR gate or an AND gate. Runs that were collected using the OR gate are referred to as singles counts, while runs collected with an AND gate are coincidence counts.
It should also be noted that during the analysis of run data the third data point collected, measured 229 days after activation, had significantly smaller activity measured. Upon reviewing calibration runs taken on the same days as yttrium measurements, it was discovered that there was an unknown error affecting the system that particular day. While this third point could be artificially boosted based on the known half-life of yttrium and has been included in some plots and tables presented later, it has been excluded from all data fits related to half-life.
Analysis of 898 keV and 1836.1 keV Lines
The 898 keV and the 1836.1 keV are the most prevalent photon energy's released in Y-88 decay. Since the total lifetime of the transition states associated with these energies are less than a picosecond, these photons are considered in coincidence for PAA analysis. The following sections describe the methods used to analyze these energy lines using singles and coincidence counting.
Singles Counting
A Simplistic Method
A simple approach to calculating the detection limit focuses on the amplitude of the energy peaks. Utilizing a data analysis program developed at CERN called ROOT, each peak was fitted to a Gaussian curve. The fit parameters provided the peak amplitude and its associated error.
The next step was to look at the need for background removal from the signal. Backgrounds subtraction is an important step to rule out noise or any spectral contribution from materials other than the sample of interest. A simple method to determine the background involves fitting the peak to a line with zero slope. The y-intercept gives the background amplitude. A weighed average of the background was calculated to be 0.0255 +/- 0.0206 Hz for the 898 keV line and 0.0072 +/-0.0120 Hz for the 1836.1 keV line. The error on the background supported the assumption that the noise had died away sufficiently to be considered zero. No background was subtracted under the simplistic method for analysis.
The peak amplitudes were next fit to the exponential equation:
,
where A is a constant, B is the slope, and t is the time since activation. Taking the inverse of the fitted slope give the calculated half-life of Y-88. The half-lives of elements are well studied and known, which meant the calculated half-life provided a check for the values calculated next.
Using the fit predators obtained from finding the half-life, it is possible to calculate the initial activity () of the sample after activation and the additional number of radioactive nuclei () in the foil. The initial activity is obtained by setting the time equal to zero in the above equation XX.XX. The detector efficiency at measuring the Y-88 energy lines needs to be taken into account. In order to do this, the activity was divided by the calculated efficiency. This will give the absolute activity of the foil. Section XX.XX provides a detailed discussion on how this value was calculated. Using the relationship between activity and the number density:
where is the decay constant, we can calculate for t=0. This value used the know half-life of Y-88, rather than the half-life obtained from fits. There should be a value agreement between the values of and found using the 898 keV and 1836.1 keV energy lines. The energy line analyzed should not affect the initial number of nuclei activated.
The next fit of interest is the signal to noise ratio (SNR). It is desirable to know how long measurements can be taken before the signal is no longer identifiable from the noise, or our SNR is equal to zero. The peak amplitudes are divided by the weighted average background and fit to a line. The linear fit is extrapolated to where it crosses the x-axis the find the time () when measurement is no longer feasible. Since the initial values and have been determined along with a final time, the decay equations
can be utilized to find the final activity and number of radioactive nuclei the can be measured by the set-up. A full summary of the results is located in section XX.XX.
A Rigorous Method
A more complicated method of analysis involves finding the integral of the energy peak by first subtracting the underlying background. The background was determined by fitting the observed window with a function that was a combination of a gaussian curve and a line. The linear fit parameters were entered into a simple program read into ROOT that subtracted the background from the histogram. The remaining signal was integrated to find the area under the peak. The values were fit to an exponential curve to obtain a calculated half-life, activity, and number density using the same approach outlined in the previous section.
The SNR was calculated by dividing the subtracted signal integral by the integrated area of the background. The data points where subjected to a linear fit and the time was extrapolated. After studying the signal to noise plot, the first data point for the singles 898 keV was much smaller and not included in the SNR fit. At the time of measurement, the background noise appears to be larger and decreases the value of the ratio. This could be from contaminants with short half-life in the sample that later decayed away. Only elements with longer half-lives, such as Y– 88, remained for the later data points. The backgrounds of the remaining three data points were averaged for the fit.
Looking for agreement between the initial values and for the 898 keV and the 1836.1 keV lines shows that they are off by a factor of 2. This more rigorous method fails for single counting. The main contributor to this method failing is believed to be the background. Using the simple method, it was determined earlier that the background noise could be considered consistently zero. The rigorous method could be giving to much weight to the zero background and driving the initial number of nuclei from agreement.
Coincidence Counting
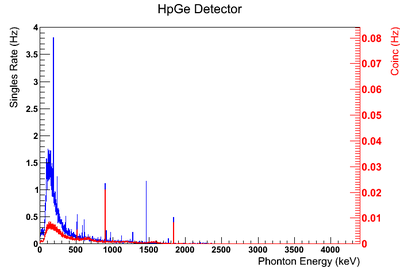
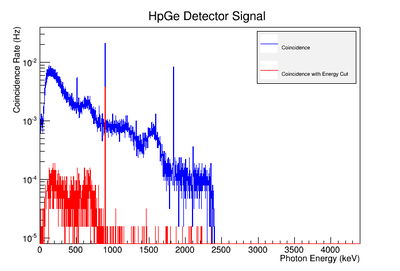
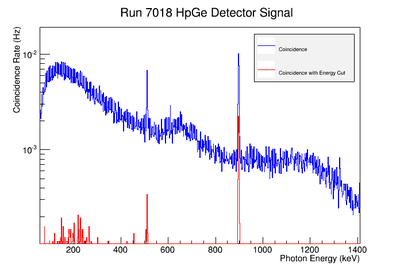
Using our Y-88 source, our set-up allows us to perform runs with the detectors in coincidence (AND mode) or singles (OR mode). Figure XX.XXa on the left shows the HpGe detector's coincidence events (red) that occurred within a 200 ns timing window. This graph has been overlaid with the same detector’s single events (blue). We can see that by having the detectors in coincidence, the noise is reduced and several peaks, which do not have multiple photons in coincidence, are removed.
The coincidence run does not show the two energy peaks associated with Y-88 decay alone. Even though we require coincidence for the system to trigger, there is still noise. These peaks could be Compton events contaminating the coincidence and accidentals. Photons can loss a portion of their energy traveling to the detector. They do not necessarily have to deposit all of their energy into the detector either. The photon can Compton scatter out. It is not possible to tell the difference between a photon that deposited all of its energy from a scattered photon, since the speed of light is so fast and the resolution of the detector so poor. The photons can, however, be distinguished if an energy cut is applied. In order to remove the Compton events and the accidentals, we can require the photon energy to be completely deposited into the detector. This can be achieved by placing an energy cut on the NaI detector around the high energy Y-88 peak in order to pull out the low energy peak and visa versa. This will remove other unwanted photon energies. Figure XX.XXb is an overlay of the coincidence signal before (blue) and after (red) an energy cut is applied to the companion detector (NaI detector). The noise seen at low energies is greatly reduced after including the cut and improved the signal.
After applying the energy cut to the NaI detector's appropriate energy line, the data was analysed using the rigorous method prescribed in the previous section. It should be noted that for the 898 keV signal to noise fit, the last data point was not included. The extended length of the run, over several days, and activities in the counting room during counting, such as refilling of the nitrogen tank, caused the peak to spread over a larger energy range. This affected the integrated area under the peak as well as the area of the background noise to be larger than expected. The backgrounds of the remaining three points were averaged for determining the SNR. A summary of the results are located in section XX.XX.
Half-Life
| Days | Energy (keV) | Integral | Statistical Error | Systematic Error | Systematic Error without Coincidence Energy Cut | |
| 108 | 1.01 | 898 | 0.0052 | |||
| 1836.1 | 0.0062 | |||||
| 159 | 1.49 | 898 | 0.0042 | |||
| 1836.1 | 0.0046 | |||||
| 229 | 2.15 | 898 | 0.0034 | |||
| 1836.1 | 0.0062 | |||||
| 245 | 2.30 | 898 | 0.0015 | |||
| 1836.1 | 0.0016 |
The signal to noise ratio is
| Days | Energy (keV) | SNR | Statistical Error | Systematic Error | |
| 108 | 1.01 | 898 | 46.181 | ||
| 1836.1 | 40.666 | ||||
| 159 | 1.49 | 898 | 37.30 | ||
| 1836.1 | 30.172 | ||||
| 229 | 2.15 | 898 | 30.195 | ||
| 1836.1 | 40.666 | ||||
| 245 | 2.30 | 898 | 37.994 | ||
| 1836.1 | 0.7569 |
Linear Fit results for ONLY the first 3 points
- 898 Sing Counting: slope = -0.16 +/- 0.019 y-intercept =54.18 +/- 3.67, t=(-54.18 +/- 3.67)/(-0.16 +/- 0.019) =337 +/- 46.07
- 1836 Sing Counting: slope = -0.29 +/- 0.042 y-intercept = 90.07 +/- 8.4, t= (-90.07 +/- 8.4)/(-0.29 +/- 0.042) = 310 +/- 53.4
- 898 Coinc Counting: slope = -0.12 +/- 0.034 y-intercept =56.02 +/- 5.76, t=(-56.02 +/- 5.76)/(-0.12 +/- 0.034) =466.8 +/- 140.7
- 1836 Coinc Counting: slope = -0.033 +/- 0.0259 y-intercept = 43.21 +/- 3.51, t= (-43.21 +/- 3.51)/(-0.033 +/- 0.0259) = 1309 +/-
- I will argue that we should ignore the slope error
Efficiencies
Singles Efficiency
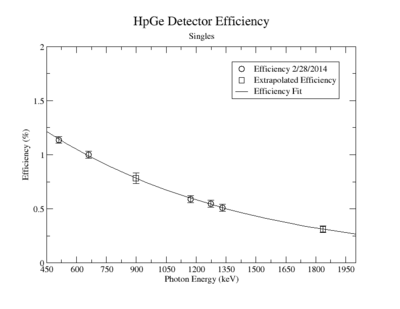
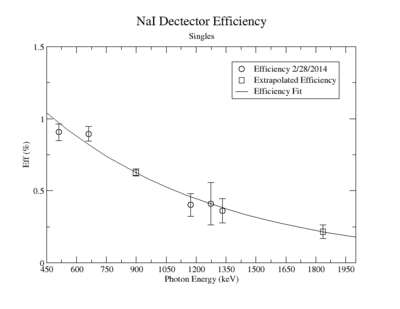
A measurement of the HpGe detectors geometric efficiency for detecting the Y-88 energy lines at 898 keV and 1836.1 keV was performed in order to determine the absolute activity of the sample. The count rate for several sources of known activity was measured by the data acquisition system. Since each sample has decayed since the original calibration by the source vendor, column 4 of tableXX.YY. reports the expected rates from each calibrated sample that were calculated using the half life and the known activity of the standard sources. The characteristic energy peaks from each source was fit to a gaussian distribution. The variance from that fit was used to determine the range of integration for the count rate measurement. The integration energy range was selected to include counts over the energy interval from to . The measured rates for each calibrated source using the HpGe detector are listed in column 5. The efficiency given by the ratio of the rates in column 5 to the expected rates in column 4 are shown in column 6 of the same table. The percent efficiency of the standard sources was fit to a exponential curve shown in figureXX.YY. The singles efficiency for 898 keV and 1836.1 keV were extrapolated from the exponential equation and are recorded in tableXX.YY. This process was repeated for the NaI detector and the results can be seen in figureXX.YY and tablesXX.YY and XX.YY.
HpGe Detector
| Run | Source | Energy | Expected rate (Hz) | HpGe Det B Rate (ADC 7) (Hz) | HpGe Eff (%) |
| 7027 | Na-22 | 511 | 1589.218 +/- 49.425 | 18.07 +/- 0.111 | 1.137 +/- 0.0317 |
| 7025 | Cs-137 | 661.657 | 2548.03 +/- 80.008 | 25.468+/- 0.172 | 0.9995 +/- 0.0321 |
| 7029 | Mn-54 | 834.848 | 41.405 +/- 1.300 | 0.485 +/- 0.014 | 1.171 +/- 0.0427 |
| 7026 | Co-60 | 1173.228 | 1876.619 +/- 58.926 | 11.03 +/- 0.106 | 0.588 +/- 0.0328 |
| 7027 | Na-22 | 1274.537 | 888.264 +/- 27.625 | 4.857 +/- 0.034 | 0.5468 +/- 0.0319 |
| 7026 | Co-60 | 1332.492 | 1878.167 +/- 58.974 | 9.584 +/- 0.023 | 0.510 +/- 0.0315 |
Extrapolated Efficiency
| Source | Energy | HpGe Eff (%) |
| Y-88 | 898 | 0.7830 +/- 0.0471 |
| Y-88 | 1836.1 | 0.3119 +/- 0.0310 |
NaI Detector
| Run | Source | Energy | Expected rate (Hz) | NaI Det B Rate (ADC 7) (Hz) | NaI Eff (%) |
| 7027 | Na-22 | 511 | 1589.218 +/- 49.425 | 14.393 +/- 0.715 | 0.9057 +/- 0.0586 |
| 7025 | Cs-137 | 661.657 | 2548.03 +/- 80.008 | 22.8 +/- 0.9154 | 0.8948 +/- 0.0510 |
| 7026 | Co-60 | 1173.228 | 1876.619 +/- 58.926 | 7.529 +/- 0.5503 | 0.4012 +/- 0.0796 |
| 7027 | Na-22 | 1274.537 | 888.264 +/- 27.625 | 3.654 +/- 0.5266 | 0.4114 +/- 0.1474 |
| 7026 | Co-60 | 1332.492 | 1878.167 +/- 58.974 | 6.784 +/- 0.5345 | 0.3612 +/- 0.0848 |
| Source | Energy | NaI Eff (%) |
| Y-88 | 898 | 0.6262 +/- 0.0246 |
| Y-88 | 1836.1 | 0.2158 +/- 0.0466 |
Coincidence Efficiency
Unlike the singles efficiency found above, the efficiency for a coincidence measurement relies on the combined efficiency of both detectors. A known Y-88 source was not available to measure the coincidence activity directly. Instead, the HpGe's geometric efficiency for detecting the Y-88 energy lines at 898 keV and 1836.1 keV was combined with the NaI detectors efficiency for the 1836.1 and 898 keV lines respectively. For example, to obtain the 898 keV coincidence efficiency, the HpGe singles efficiency at this energy line is multiplied by the NaI singles efficiency at the 1836.1 keV line. The uncertainties of the singles efficiency are added in quadrature and the resulting values recorded in column 4 of tableXX.YY. The reverse case was applied to find the coincidence efficiency at the 1836.1 keV line and the values are listed in column 4 of tableXX.YY.
| Source | HpGe Singles 898 keV Eff (%) | NaI Singles 1836.1 keV Eff (%) | HpGe Coincidence Eff (%) |
| Y-88 | 0.7830 +/- 0.0471 | 0.2158 +/- 0.0466 | 0.001690 +/- 0.00038 |
| Source | HpGe Singles 1836.1 keV Eff (%) | NaI Singles 898 keV Eff (%) | HpGe Coincidence Eff (%) |
| Y-88 | 0.3119 +/- 0.0310 | 0.6262 +/- 0.0246 | 0.001953 +/- 0.00021 |
Summary
| Energy | Trig | (days) | (before efficiency) (Hz) | (before efficiency) (nuclei) | (after efficiency) (Hz) | (after efficiency) (nuclei) | (days) | (Hz) | (nuclei) | |
| 898 | sing | 127.668 +/- 16.8095 | 2.3901 +/- 0.417 | 3.177e7 +/- 5.543e6 | 305.252 +/- 55.1726 | 4.057e9 +/- 7.333e8 | 337.209 | 34.0937 +/- 19.0496 | 4.532e8 +/- 2.532e8 | 0.1117 +/- 0.0656 |
| coin | 108.18 +/- 4.89 | 0.0154 +/- 0.0003 | 204958.085 +/- 4201.641 | 912.453 +/- 63.3215 | 1.213e10 +/- 8.416e8 | 483.60 | 39.3503 +/- 9.51009 | 5.230e8 +/- 1.264e8 | 0.0431 +/- 0.0108 | |
| 1836.1 | sing | 107.273 +/- 17.3321 | 1.2838 +/- 0.1451 | 1.706e7 +/- 1.928e6 | 411.606 +/- 48.2299 | 5.471e9 +/- 6.410e8 | 308.569 | 55.3799 +/- 8.73541 | 7.361e8 +/- 1.161e8 | 0.1345 +/- 0.0264 |
| coin | 100.10 +/- 4.0 | 0.0196 +/- 0.0004 | 260440.778 +/- 5339.036 | 1003.32 +/- 44.7396 | 1.334e10 +/- 5.946e8 | 305.63 | 137.594 +/- 29.7812 | 1.829e9 +/- 3.958e8 | 0.1371 +/- 0.0303 |
Average : 2.446e9 +/- 3.472e8
Error analysis
1.) rate energy cuts
2.) Energy calibration error
3.) Linear background fit error
4.) Gaussian integration of Signal - background peak
5.) ignorable error from run length time
6.) Coincidence energy cut.
7.) dividing by average background for SNR
8.) correction ratio for 3rd data point
9.) error in half life to find N0 for the detection limit extrapolation
10.) error extrapolation efficiency to higher energy lines for N0 calculation
Energy Window systematic error
The signal is measured by subtracting a count rate that is summed over an energy interval. The choice of this integration interval, energy window, is a source of systematic error. In order to calculate the error associated with the energy window, its range was adjusted based on the statistical variance of the background subtracted count rate fit to a gaussian. The integral was measured for window ranges chosen according to an integer interval of the standard deviation , where n = 3,4,5. The difference between the largest and mid-value was taken as the positive standard deviation, and the lowest was used for the standard deviation negative fluctuation. The resulting errors were divided by the signal to obtain a percent error as shown in column 1 of TableXXX.
Energy calibration systematic error
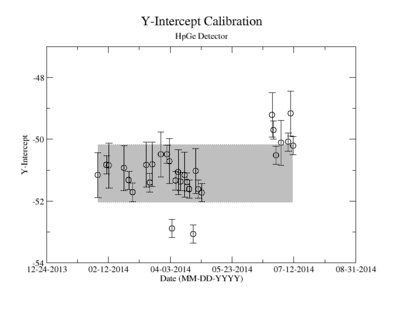
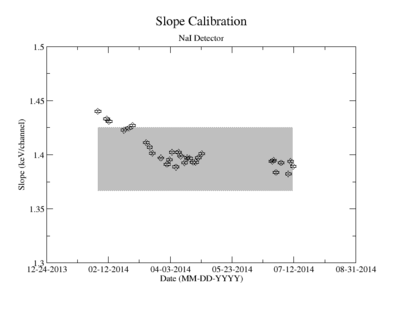
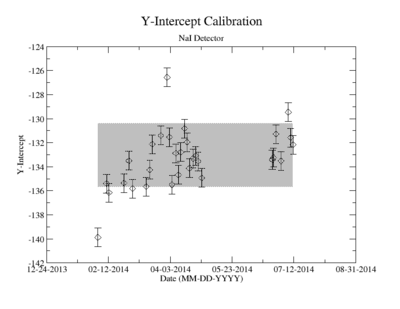
Prior to each measurement of the Y-88 sample's activity, the detectors where calibrated using several standard sources with known activity and dominant energy lines. This was accomplished by counting certified samples of Cs-137, Co-60, and Na-22 as well as Ba-133 and Mn-54. The observed mean ADC channel number was correlated with the expected energy line from each of the above sources. The correlation was measured using a standard linear fit algorithm. The linear fit algorithm determines the uncertainty of each fit parameter, the slope and the y-intercept. The effects of this uncertainty on the signal was analysed and is referred to as the energy calibration error.
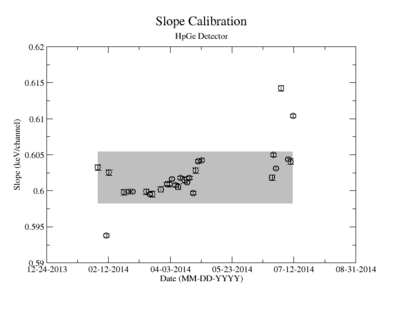
The uncertainty in the energy calibration just before a singles measurement was used to investigate the impact of the calibration on the measured signal for a given energy window of integration. While the singles measurements took less than 10 minutes, the coincidence measurement required more than 24 hours. The long term variance of the energy calibration shown in Figure ZZ.XXX was used to estimate the impact of the energy calibration drift during the coincidence measurements. The fit's y-intercept has a temporal variance corresponding to a relative uncertainty of about 1.865%; the slope is about 0.608%. The effects of this error on the coincidence signal were analysed. In both cases, the range of the energy widow is held constant while the slope and the y-intercept where adjusted to account for all possible combinations with and without their respective uncertainty. The integral value was recorded after every fit parameter change and the max, min, and mean values were obtained. The difference between the largest and mean value was taken as the positive standard deviation, and the lowest was used for the standard deviation's negative fluctuation. The resulting errors were divided by the signal to obtain a percent error as shown in column 2 of TableXXX.
Linear Fit Systematic error
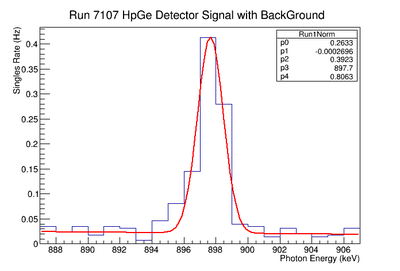
The signal is determine by subtracting the underlying background. A estimate of this background is made by fitting the observed count rate with the function below :
.
The above function contains a Gaussian representing the measured signal and a linear function for the background. The above figure XX.YY shows the fit applied. The linear fit parameters are used to create a histogram that is subtracted from the raw signal histogram, resulting in a histogram of just a signal. The energy window range used for the fit was adjusted and several fits performed to determine the uncertainty of the fit's slope and y-intercept. This systematic error, based on the fits dependence on the energy window is shown in the table under the column labeled "Linear Fit of Background". The fit parameters where adjusted to determine the maximum and minimum area of the background. For minimum background area, it was required that the area be positive. The difference between the maximum and unadjusted area value was taken as the positive standard deviation's fluctuation, and the minimum was used for the standard deviation's negative fluctuation. The resulting errors were divided by the signal to obtain a percent error as shown in column 3 of TableXXX.
Systematic error of the Coincidence Energy Cut
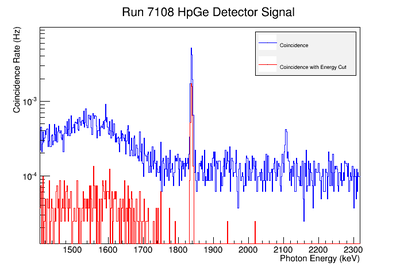
Figure AAA.XXX below show the coincidence measurements made before(blue) and after(red) energy cuts are applied on the NaI signal to reduce the accidental coincidence events and photons that fail to deposit all their energy in the NaI detector due to compton scattering.
To analyze the error association with coincidence counting only, the signal on the NaI detector was fit to a gaussian distribution. The of the gaussian fit was used to adjust the energy cut limits. The energy window was set at . The intergal values were recorded for each instance and the difference between the maximum and unadjusted integral values were taken as the positive standard deviation's fluctuation while the minimums were used for the standard deviation's negative fluctuation. The resulting errors were divided by the coincidence signal to obtain a percent error as shown in column 5 of TableXXX. The limited energy resolution of the NaI detector makes this uncertainty the dominant systematic error. If two HpGe detectors are used, then this uncertainty would decrease substantially will be far less than the remaining dominant systematic error; the energy Gaussian integral uncertainty. We report this systematic uncertainty but it is not propagated for the final result in order consider the case of a coincidence apparatus using two HpGe detectors.
Half-life
898 keV Singles
| Days | Trig | Energy Window | Energy Calibration | Linear Fit of Background | Gaussian Integration of Signal | Total Systematic Error | |
| 108 | 1.01 | sing | |||||
| 159 | 1.49 | sing | |||||
| 229 | 2.15 | sing | |||||
| 245 | 2.30 | sing |
898 keV Coincidence
| Days | Trig | Energy Window | Energy Calibration | Linear Fit of Background | Gaussian Integration of Signal | Coincidence Energy | Total Systematic Error | Systematic Error without Coincidence Energy Cut | |
| 108 | 1.01 | coin | |||||||
| 159 | 1.49 | coin | |||||||
| 229 | 2.25 | coin | |||||||
| 245 | 2.30 | coin |
1836.1 keV Singles
| Days | Trig | Energy Window | Energy Calibration | Linear Fit of Background | Gaussian Integration of Signal | Total Systematic Error | |
| 108 | 1.01 | sing | |||||
| 159 | 1.49 | sing | |||||
| 229 | 2.15 | sing | |||||
| 245 | 2.30 | sing |
1836.1 keV Coincidence
| Days | Trig | Energy Window | Energy Calibration | Linear Fit of Background | Gaussian Integration of Signal | Coincidence Energy Cut | Total Systematic Error | Systematic Error without Coincidence Energy Cut | |
| 108 | 1.01 | coin | |||||||
| 159 | 1.49 | coin | |||||||
| 229 | 2.15 | coin | |||||||
| 245 | 2.30 | coin |
Systematic error in the SNR
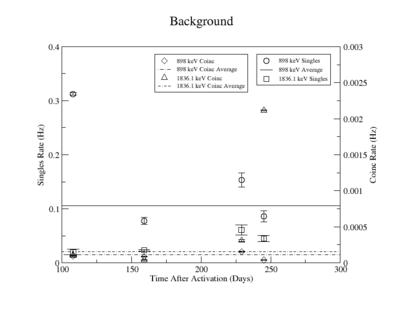
The singles measurement of the 898 keV peak had an initial high background that decays quickly and was more or less constant for singles measurements take 159 days after irradiation. We assumed that this reflected the presence of activated material with half lives longer that 245 days. As a result the background for the last three measurements was averaged and used in the denominator for the SNR. The first singles measurement has a large background due to activated nuclei with short half lives. This background decreased substantially after about 51 days when the next measurement was taken (the half-life of Y-88 is 106.6 days). The singles background near the 1836 keV line was measured to be around 0.5 Hz and fluctuated less over the experiment compared to the background around the 898 peak. The coincidence measurements had such little background, due to the nature of the apparatus, that the background was averaged over the first three measurements for both the 898 and the 1836 peaks separately. The background for the final coincidence measurements was ignored because of the increased noise produced when the detectors nitrogen dewar was filled during the 5 day background measurement.
The systematic uncertainty of the background was not analysed and propagated into the final SNR uncertainty. The signal's total systematic error, described above, was used for the final uncertainty.
Signal to Noise Ratio
| Energy (keV) | Trig | Variance of Averaged Background |
| 898 | sing | |
| coin | ||
| 1836.1 | sing | N/A |
| coin |
The background's systematic error is being ignored.
Background contribution to the SNR error
The analysis of the background uncertainty is described in the above section, "Linear Fit Systematic error." The background's relative statistical uncertainty shown in column 5 of TableXXX is calculated by varying the integral of the background by the uncertainties from the fit and dividing by the background used for the SNR ratio calculation. Column 6 presents the uncertainty of the averaged background as mentioned in the previous section. The variance the coincidence measurement is considerable larger than the individual coincidence measurements. The background in each singles measurement is smaller than the average variance indicating that the individual background measurements could have been made longer to improve their statistical uncertainty.
898 keV Background
| Days | Trig | Background | Linear Fit of Background Error | Statistical Error of Averaged Background | |
| 108 | 1.01 | sing | 0.3123 | N/A | |
| coin | 9.518e-5 | ||||
| 159 | 1.49 | sing | 0.0777 | ||
| coin | 8.732e-5 | ||||
| 229 | 2.15 | sing | 0.1532 | ||
| coin | 1.554e-4 | ||||
| 245 | 2.30 | sing | 0.0862 | ||
| coin | 3.948e-5 |
1836 keV Background
| Days | Trig | Background | Linear Fit of Background Error | Statistical Error | |
| 108 | 1.01 | coin | 1.037e-4 | ||
| 159 | 1.49 | coin | 4.248e-5 | ||
| 229 | 2.15 | coin | 3.112e-4 | ||
| 245 | 2.30 | coin | 2.114e-3 |
Results and Conclusion
This thesis quantified the detection limit improvement of coincidence photon activation analysis (CPAA) over the standard photon activation analysis method (PAA). Background is one of the most important contributions to establishing a detection limit. One way that a detection limit can be improved is to reduce the background. This can be accomplished by requiring the detection of two photons in coincidence, since the background is typically composed of random events. The detection limit was defined as the point at which the signal could not be distinguished from background. In Chapter 3, the time when the background subtracted signal could no longer be measured ($t_{final}$) was determined for both PAA and CPAA measurements of the same sample. This final time, along with a calculated initial value ($N_0$), is used to find the lowest number of activated nuclei, the detection limit, that PAA and CPAA can measure.
Efficiency for Converting Y-89
The concept of photon activation analysis relies on activating a nucleus by using a high energy photon to eject one or more nucleons (protons or neutrons). The nuclei that have had one or more nucleons removed are typically unstable and decay. It is well understood that radioactive materials decay as an exponential function of time. The measured signals of the Y-88 sample were fit to an exponential curve to find the initial number of activated atoms in the foil. The exponential fit was extrapolated back to the initial time $t=0$ when the foil was activated. The half-life of Y-88 is well known, 106.63 days, and was used to calculate the decay constant $\lambda$. Using the relationship between activity and the number density, $A = \lambda N$, the initial value, $N_0$, can be found for time $t=0$.
The Yttrium foil's mass was found to be 0.0288 +/- 0.0002 g. Using Avogadro's number, $N_a$, and the isotopic mass of Y-89, $m_i=88.905848 \frac{g}{mol}$, the number of atoms (N) was found using:
\begin{equation} N = \frac{m N_a}{m_i}. \label{eq:number density} \end{equation}
The foil contained $(195.1 \pm 1.35)\times 10^{18}$ atoms of Y-89. Taking the ratio of $N_0$ and the number of atoms gives the accelerator beam's efficiency at activating the sample. Using the above number of atoms and using the average of $N_0$ for singles and coincidence events, the ratio was $(24.42 \pm 5.26)\times 10^{-12}$ using singles and $(65.28 \pm 5.41)\times 10^{-12}$ using coincidence. For every $10^{12}$ atoms of Y-89, one atom of Y-88 was produced.
Minimum Number of Y-88 Atoms Detectable
After activating a source, a time will be reached when the signal is no longer observable due to background. The lowest activity of Y-88 that the apparatus could measure was predicted by extrapolating the measured signal to noise ratio (SNR) forward in time until it was zero. Details on finding the signal to noise ratio can be found in Chapter~\ref{Data Analysis}. Beyond this point in time ($t_{final}$), the signal will not be distinguishable from the background noise and measurements will no longer be possible with this apparatus. The average value of $N_0$, $(8.75 \pm 2.02)\times 10^9$ nuclei, and the time when the SNR reached zero were used in the exponential decay function $N(t) = N_0 e^{-\lambda t}$ to find the lowest measurable activity, N($t_{final}$), using singles and coincidence counting. The 898 keV energy line resulted in a N($t_{final}$) of $(9.77 \pm 2.35)\times 10^8$ nuclei after 337.209 days using singles counting and $(3.77 \pm 0.954)\times 10^8$ nuclei after 483.60 days using coincidence counting. For the 1836.1 keV energy line, N($t_{final}$) was $(11.77 \pm 2.93)\times 10^8$ nuclei after 308.569 days with singles counting. Using this apparatus, coincidence counting can measure half of the singles minimum number of detectable atoms. The detection limit can be improved by at least a factor of two using coincidence counting over standard PAA.
Appendix: Methods
The atomic methods listed in Table~\ref{tab:Detection_Limit} are briefly described in the following sections.
Inductively coupled plasma mass spectrometry(ICP-MS)
Inductively coupled plasma mass spectrometry (ICP-MS) is an elemental analytical technique that combines a high-temperature ICP plasma with a mass spectrometer. A sample is introduced into the ICP plasma, typically as an aerosol, where it ionizes the sample's atoms. The ions are then brought into the mass spectrometer and focused by electrostatic lenses in the system. Once in the mass spectrometer, the ions are separated by their mass-to-charge ratio. The most commonly used type of mass spectrometer is the quadrupole mass filter. The ability to filter ions this way allows the ICP-MS to supply isotopic information, since different isotopes of the same element have different masses. Once the ions have been separated by their mass-to-charge ratio, they must then be detected or counted by a suitable detector. A channel electron multiplier (CEM) was used in early ICP-MS instrumentation, however, this open glass cone coated with a semi-conductor has since been replaced with discrete metal dynode type detectors. The ICP-MS system has detection limits that range from to 0.001 parts-per-million (ppm).
https://www.uam.es/personal_pas/txrf/imagenes/tutorial10.pdf
Inductively coupled plasma atomic emission spectroscopy(ICP-AES)
Inductively coupled plasma atomic emission spectroscopy (ICP-AES) is sometimes referred to as ICP-OES, meaning 'optical emission spectrometry'. Similar to ICP-MS, it utilizes the ICP plasma to produce exited atoms and ions that will emit electromagnetic radiation at wavelengths characteristic of a particular element. The concentrations of the elements within a sample can be determined based on the intensity of the emissions. The ICP-AES is composed of a ICP and the optical spectrometer. As with ICP-MS, a liquid or organic sample is injected into the hot plasma torch, where compounds are usually completely dissociated. The excited atoms and ions emit radiation at characteristic lines which are focused onto a diffraction grating and slit system where it is dispersed into its component wavelengths in the optical spectrometer. The photomultiplier tubes previous used to measure the light intensity have been replaced by an array of semiconductor photodetectors such as solid state charge-coupled devices (CCDs). The intensity of each line is compared to previously measured intensities of known concentrations of the elements in order to calibrate the system. ICP-AES has been used to measure trace metals metal concentrations ranging from to 1 ppm.
Atomic Absorption Spectrometry (multi-element AAS)
Atomic absorption spectrometry (AAS) is a spectra-analytical procedure used for the determination of elements to within ppm by using the absorption of optical radiation by the atoms. AAS can be used to determine over 70 different elements in solution, but the technique can only measure one element at a time. In order to analyze an element, a liquid sample must be atomized into a vapor. The most common atomizers are flames and electrothermal graphite tube atomizers. Since AAS basic mode of operation is absorption, as opposed to emission, optical radiation that is characteristic of the element to be determined is passed through the sample vapor. A hollow cathode lamp is the most common radiation source in AAS, and most machines utilize two lamps to cover more elements. The radiation then passes into a monochromator, either a prism or diffraction grating, followed by a slit in order to separate the element-specific radiation from any other radiation emitted by the radiation source. The optical radiation is then transmitted to a photomultiplier detector to convert the light into an electrical current.
Particle-induced X-ray Emission (PIXE)
Particle-induced X-ray Emission (PIXE) is a non-destructive analytical technique used in determining elemental composition of a material or sample. It has detection limits typically around ppm. The particle beam most often used for PIXE is a positive ion beam. Three types of spectra can be collected using PIXE: X-ray emission spectrum, Rutherford backscattering spectrum, and proton transmission spectrum. The proton beam strikes a sample, which causes inner shell vacancies. The outer shell electrons de-excite to replace, or fill, the inner shell vacancies, emitting radiation in the X-ray portion of the electromagnetic spectrum. The energy of the emitted photon characteristic of the atom. These emissions are detected using energy-dispersive detectors. Protons in the ion beam will also experience elastic collisions, Rutherford backscattering, with the nucleus of the atom. The backscatter can give composition information on the sample and allow for correction of the X-ray photon loss within the sample. Proton transmission can further provide information about the sample.
X-ray Fluorescence Spectrometry (XRF)
X-ray Fluorescence Spectrometry (XRF) is an analytical technique used for elemental analysis, particularly in the investigation of metals, glass, and ceramics. In XRF, the primary X-Rays are most commonly produced by an X-ray tube and have detection limits around ppm. However, alternative primary sources include synchrotron radiation, with reported detection limits of 100 ppm or better, can be used. The synchrotron is a large electron accelerator which produces electromagnetic radiation across the whole spectrum, with high spectral purity and high beam intensity. Desired sections of the spectrum can be selected and focused while retaining beam intensity. This beam can then be used as the primary beam in XRF analysis. Once the primary X-rays strike the solid sample, two processes occur, scattering and absorption. Vacancies are created in the orbital shell of the sample atoms as a result of energy absorption and the ejection of an electron. The removal of an electron makes the structure of the atom unstable, and electrons in higher orbitals will de-excite to the lower orbital to fill the vacancy. During the change in orbital, radiation is emitted with energy characteristic of the atom present. This secondary radiation from the sample can be analyzed with two different approaches, energy-dispersive or wavelength-dispersive analysis. In energy-dispersive analysis, various types of solid state detectors are used to collect the incoming X-ray photon, while wavelength-dispersive analysis employs a monochromator and a photomultiplier for detection of a single wavelength of radiation.
10-100 PPM using Xray tubes
100 ppm or better using synchrotron
Ba-133 CAA
Useful commands
Converting CODA data file to ROOT
make sure the CODA and ROOT environmental variables are setup by source the following scripts
source ~/CODA/setup
source ~/ROOT/root/bin/thisroot.csh
Now change to the data subdirectory and execute the program to convert the data file to root
cd /data
~/CODA/CODAreader/ROOT_V5.30/V785V792/evio2nt -fr6994.dat > /dev/null
rename the file so it has the .root extension allowing ROOT to identify it in the browser
mv r6994 r6994.root
Calibration work
ADC7 Average Slope = 0.601839 +/- 0.003662033
ADC7 Average Y-intercept = -51.1025 +/- 0.953309
ADC3 Average Slope = 1.39597 +/- 0.029539420
ADC3 Average Y-Intercept = -133.007 +/- 2.66636
System's intrinsic err
Plot calibration parameters as a function of time
determine the variance of the parameters using several (>20) fits
Impact of higher order fits
Plot
Variance comes from several fits,.
Compare uncertainty when fit is E-vs-Channe to Channel-vs-E
Probably should use %error for the weighting
Concentration measurement
A comparison of the measure concentrations using singles and coincidence counting
Final problems to sort out
- Singles N_0 is equal before efficiency for the two different energies and then x2 different after efficiency? Singles should differ by factor of 2 before efficiency is corrected.AW_Singles_Prob_Y88_2015
- Detection limit very small
- Y-88 production efficiency ( 10^{-12})compared to X-sect (.76 barns) , need to know photon flux