2NCorr Photon flux estimate
Overview
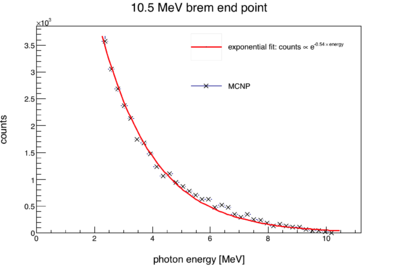
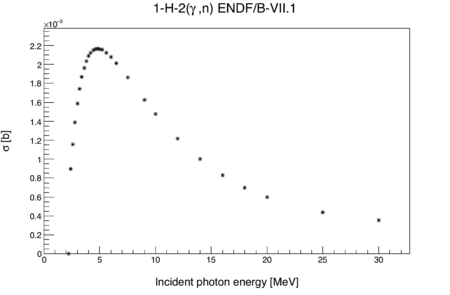
An estimated lower bound for the photon flux throughout the experiment can be calculated from the data of a D2O target. The measured neutron rate from D2O depends on the following: the (G,n) cross-section as a function of energy, the energy distribution of the brem photons, target geometry, detector efficiency, and photon flux. The (G,n) cross-sections are known and the brem energy distribution can be taken from an MCNP simulation. The only remaining unknown variables are photon flux and detector efficiency. By setting detector efficiency to 100%, and considering only geometric effects (i.e. solid angle), a lower bound can be placed on the photon flux incident on all targets.
Plots
Calculation
The measured neutron rate is given by:
- is the number of photons incident on the target with energy greater than 2.3 MeV, the threshold for photo-disintegration of D2O.
- is photon energy as a function
- is the detector efficiency for D2O photo-neutrons, integrated over the neutron energy spectrum.
- is the probability of a photo-disintegration event given that the photon has energy E.
- is the probability of a photon having energy E, given that the photon is above threshold.
- is the mean number of neutrons observed per pulse (1.74E-2).
- is the solid angle for the entire detector array (0.056/4pi).
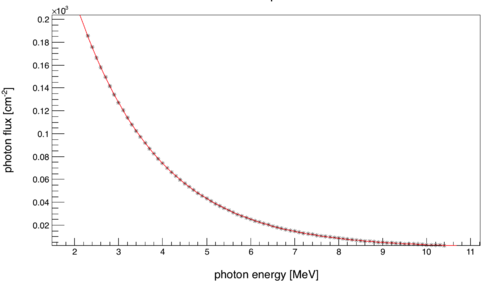
Now writing in terms of the cross-section and substituting a normalized photon energy distribution taken from MCNP in place of , the above becomes:
The integral above was calculated numerically with software.
The unknown detector efficiency can be set to 1, which brings to its theoretical minimum, or roughly 1,000 photons per pulse. The detector efficiency is not known exactly, but it lies within the range of 5-25%, so there are between 4,000 and 20,000 photons above 2.3 MeV incident on the target. Each photon can be considered an independent "binomial trial", and with such a large number of such trials, Poissonian distribution is a good approximation for the probability distribution of the number of photo-nuclear reactions in a given pulse.