Four-vector Algebra

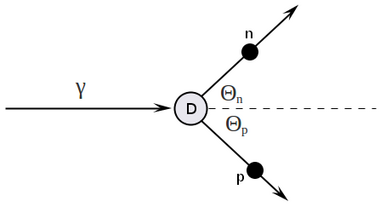
Let's do the four-vector algebra:

[math] p_{\gamma} = \left( T_{\gamma},\ T_{\gamma},\ 0,\ 0  \right) [/math] 
[math] p_D     = \left( m_D,\ 0,\ 0,\ 0  \right) [/math] 
[math] p_{n} = \left( E_n,\ \ p_n\cos \Theta_n,\ \ p_n\sin \Theta_n,\ \ 0  \right) [/math] 
[math] p_{p} = \left( E_p,\ \ p_p\cos \Theta_p,\ \ p_p\sin \Theta_p,\ \ 0  \right) [/math]

By conservation of four-momentum:

[math] p^{\mu}_{\gamma} + p^{\mu}_D = p^{\mu}_p + p^{\mu}_n\ \ \Rightarrow \ \  p^{\mu}_p = p^{\mu}_{\gamma} + p^{\mu}_D - p^{\mu}_n[/math]

Squaring both side of equation above and using the four-momentum invariants [math](p^{\mu})^2 = m^2[/math] we have:

[math] m_p^2 = m_D^2 + m_n^2 +  2T_{\gamma}\cdot m_D  - 2m_D\cdot E_n - 2\left( T_{\gamma}E_n - T_{\gamma}p_n\cos\Theta_n\right) [/math]

Energy dependence of [math]E_\gamma[/math] as function of neutron energy [math]E_n[/math] and neutron angle [math]\Theta_n[/math]

We can easily solve the equation above with respect to incident photon energy:

[math]T_{\gamma} = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D E_n}{2\ (m_D - E_n + p_n cos\Theta_n)} [/math]

Detector is located at [math]\Theta_n = 90^o[/math], so

[math]T_{\gamma} = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D E_n}{2\ (m_D - E_n)} =  \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D (T_n + m_n)}{2\ (m_D - (T_n + m_n))}[/math]

For non-relativistic neutrons [math]T_n \ll m_n = 939.5\ MeV[/math], and we can neglect the [math]T_n[/math] in denominator, so

[math]T_{\gamma} = \frac {m_p^2 - m_n^2 - m_D^2 + 2\ m_D m_n + 2\ m_D T_n}{2\ (m_D - m_n)} [/math]

Substituting the corresponding masses, we get finally for the case of non-relativistic neutrons detected at the angle [math]\Theta_n = 90^o[/math]:

[math]T_{\gamma}\ [MeV] = 2.003\ T_n\ [MeV] + 1.577\ [MeV][/math]

and visa versa:

[math]T_n\ [MeV] = 0.499\ T_{\gamma}\ [MeV] - 0.787\ [MeV][/math]

Using the formulas above we can:

1. Calculate the threshold for [math]^2D(n,\gamma)[/math] reaction:

[math]E_{\gamma} = 1.577\ MeV[/math]

2. Predict the incident photon energy based on the detected neutron energy.

3. Predict the detected neutron energy based on the incident photon energy.

  For the incident photons up to 25 MeV we have (0 - 11.69) MeV neutrons

  For the incident photons up to 44 MeV we have (0 - 21.17) MeV neutrons

Also note:

and visa versa

 [math] T_n = \frac {2\ T_{\gamma}\ m_D + m_D^2 + m_n^2 - m_p^2} {2\left( T_{\gamma} + m_D \right)} - m_n[/math]

how it looks

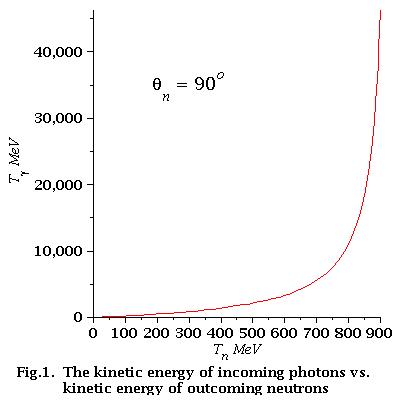
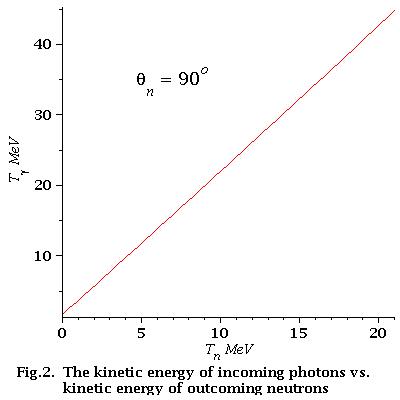
low energy approximation=

As we can see from Fig.2 for low energy neutrons (0-21 MeV)

energy dependence of incident photons is linear

Find that dependence. We have:

[math] T_{\gamma}(0\ MeV) = 1.715360792\ MeV [/math]
[math] T_{\gamma}(21\ MeV) = 44.78703086\ MeV [/math]

So, the equation of the line is:

[math] T_{\gamma}
      = \frac{T_{\gamma}(21\ MeV) - T_{\gamma}(0\ MeV)}{21\ MeV - 0\ MeV}\ T_n + T_{\gamma}(0\ MeV) [/math]

Finally for low energy neutrons (0-21 MeV):

[math] T_{\gamma} = 2.051\ T_n + 1.715 [/math]

example of error calculation

==example 1=+

Say, we have, 10 MeV neutron with uncertainty 1 MeV, the corresponding uncertainly for photons energy is:

[math] \delta T_{\gamma} = 2.051\ \delta T_n = 2.051\times 1\ MeV = 2.051\ MeV [/math]

example 2

Say, the neutron's time of flight uncertainly is 1 ns

The neutron's kinetic energy is:

[math]T_n = m_n (\gamma - 1) = m_n\left[ \frac{1}{\sqrt{1-\left(\frac{l}{c\ t}\right)^2}} - 1 \right][/math]

And:

[math]\delta T_n \left(\delta t\right) = -\ \frac{m\ l^2 \delta t}{\left(1-\left(\frac{l}{c\ t}\right)^2\right)^{3/2}c^2 t^3}[/math]

Also we need the neutron's time of flight as function of neutron's kinetic energy:

[math]t:=\frac{l}{c\ \beta_n} = \frac{l}{c\ (p_n/E_n)} =
         \frac{l\ (T_n + m_n)}{c\sqrt{T_n^2+2m_nT_n}}[/math]

Say, we have 10 MeV neutron, 1 m away detector, and neutron's time of flight uncertainty is 1 ns. Then the neutron time of flight is:

[math]t(T_n = 10\ MeV) = 23\ ns[/math]

Neutron kinetic energy errors are:

[math]\delta T_n(\delta t = 1\ ns) = 0.88\ MeV[/math]
[math]\frac{\delta T_n}{T_n} = \frac{0.88\ MeV}{10\ MeV} = 8.8\ %[/math]

And photon energy errors are:

[math]\delta T_{\gamma} = 2.051\cdot \delta T_n = 2.051\cdot 0.88\ MeV = 1.81\ MeV [/math] 
[math]\frac{\delta T_{\gamma}}{T_{\gamma}} = \frac{1.80\ MeV}{(2.051\cdot 10 + 1.715)\ MeV} = 8.1\ %[/math]

Below are some examples for different detector distance and neutron kinetic energy:

[math]\delta t_n[/math]	[math]l[/math]	[math]T_n[/math]	[math]\beta_n[/math]	[math]t_n[/math]	[math]\delta T_n[/math]	[math]\frac{\delta T_n}{T_n}[/math]	[math]\delta T_{\gamma}[/math]
1 ns	1 m	5 MeV	0.103	32 ns	0.31 MeV	6.2 %	0.64 MeV	5.3 %
1 ns	1 m	10 MeV	0.145	23 ns	0.88 MeV	8.8 %	1.81 MeV	8.1 %
1 ns	1 m	20 MeV	0.203	16 ns	2.51 MeV	12.6 %	5.16 MeV	12.1 %
1 ns	1 m	0.5 MeV	0.033	102 ns	0.010 MeV	1.9 %
1 ns	1 m	1 MeV	0.046	72 ns	0.028 MeV	2.8 %
1 ns	1 m	2 MeV	0.065	51 ns	0.078 MeV	3.9 %
1 ns	1 m	4 MeV	0.092	36 ns	0.22 MeV	5.5 %

Go Back

Neutron Polarimeter

Contents