Go Back
Relativistic kinematic
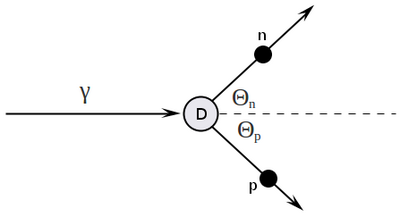
energy dependence of outcoming neutron versus energy of incoming photons
[math] E = T + m[/math]
[math] E = p^2 + m^2[/math]
writing four-vectors:
[math] p_{\gamma} = \left( T_{\gamma},\ T_{\gamma},\ 0,\ 0 \right) [/math]
[math] p_D = \left( m_D,\ 0,\ 0,\ 0 \right) [/math]
[math] p_{n} = \left( E_n,\ p_n\cos(\Theta_n),\ p_n\sin(\Theta_n),\ 0 \right) [/math]
[math] p_{p} = \left( E_p,\ p_p\cos(\Theta_p),\ p_p\sin(\Theta_p),\ 0 \right) [/math]
Doing four-vector algebra:
[math] p^{\mu}_{\gamma} + p^{\mu}_D = p^{\mu}_p + p^{\mu}_n \Rightarrow [/math]
[math] p^{\mu\ 2}_p = \left(p^{\mu}_{\gamma} + p^{\mu}_D - p^{\mu}_n\right)^2 =
p^{\mu\ 2}_{\gamma} + p^{\mu\ 2}_D + p^{\mu\ 2}_n +
2\ p^{\mu}_{\gamma}\ p^{\mu}_D - 2\ p^{\mu}_{\gamma}\ p^{\mu}_n - 2\ p^{\mu}_D\ p^{\mu}_n [/math]
[math] m_p^2 - m_{\gamma}^2(=0) - m_D^2 - m_n^2 = [/math]
[math] = 2\ T_{\gamma}\ m_D - 2\left( T_{\gamma}\ E_n - T_{\gamma}\ p_n\cos(\Theta_n)\right) - 2\ m_D\ E_n [/math]
[math] = 2\ T_{\gamma}\left( m_D - E_n + p_n\cos(\Theta_n) \right) - 2\ m_D\ E_n [/math]
Finally we have:
<math> T_{\gamma} = \frac {2\ m_D\ E_n + m_p^2 - m_D^2 - m_n^2} {2\ \left( m_D - E_n + p_n\cos(\Theta_n) \right)}<\math>
Because our detector <math><\math>
Go Back