Forest Relativity Notes

Lorentz Transformations

The picture below represents the relative orientation of two different coordinate systems [math](S, S^{\prime})[/math] . [math]S[/math] is at rest (Lab Frame) and [math]S^{\prime}[/math] is moving at a velocity v to the right with respect to frame [math]S[/math].

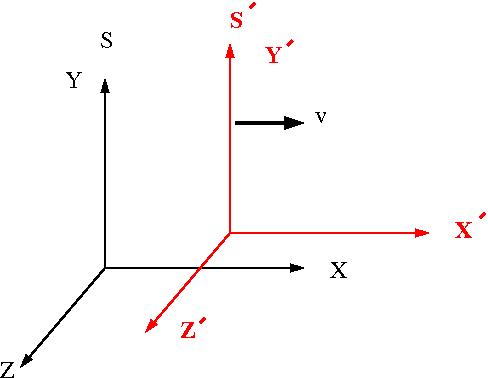
The relationship between the coordinate[math] (x,y,z,ct)[/math] of an object in frame [math]S[/math] to the same object described using the coordinates [math](x^{\prime},y^{\prime},z^{\prime},ct^{\prime})[/math] in frame [math]S^{\prime}[/math] is geven by the Lorentz transformation:

4- vector notation

The 4-vector notation is given as

[math]x^{\mu^{\prime}} = \sum_{\nu=0}^3 \Lambda_{\nu}^{\mu} x^{\nu}[/math]

where

[math] x^0 \equiv ct[/math]

[math]x^1 \equiv x[/math]

[math]x^2\equiv y[/math]

[math]x^3\equiv z[/math]

[math]\Lambda = \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ][/math]

[math]\beta = \frac{v}{c} = \frac{pc}{E}[/math]

[math]\gamma = \frac{1}{\sqrt{1 -\beta^2}} = \frac{E_{tot}}{mc^2}[/math]

NOTE

It is common in particle physics to define [math] c \equiv 1[/math] making [math]\gamma = \frac{E}{m}[/math] where [math]m[/math] is in units of [math]\frac{\mbox{MeV}}{\mbox{c}^2}[/math]

example

[math]x^{0^{\prime}} = \sum_{\nu=0}^2 \Lambda_{\nu}^0 x^{\nu} = \Lambda_0^0 x^0 + \Lambda_1^0 x^1 \Lambda_2^0 x^2 + \Lambda_3^0 x^2[/math]

[math]ct^{\prime}= \gamma x^0 - \gamma \beta x^1 + 0 x^2 + 0 x^3 = \gamma ct - \gamma \beta x = \gamma(ct -\beta x)[/math]

Or in matrix form the tranformation looks like

[math]\left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix} \right )[/math]

Note

Einstein's summation convention drops the [math]\sum[/math] symbols and assumes it to exist whenever there is a repeated subscript and uperscript

ie; [math]x^{\mu^{\prime}} = \Lambda_{\nu}^{\mu} x^{\nu}[/math]

in the example above the[math] \nu[/math] symbol is repeated thereby indicating a summation over [math]\nu[/math].

Momentum 4-vector

[math]p^{\mu} \equiv (\frac{E}{c} , \vec{p})[/math]

[math]p_{\mu} \equiv (\frac{E}{c} , -\vec{p})[/math]

[math]p_{\mu}p^{\mu} = \frac{E^2}{c^2} - p^2 \equiv E^2 - p^2 = m^2[/math]

Note

There is another convention used for 4-vector notation by Perkins and Koller which goes like this

[math]p^{\mu} \equiv (\vec{p},iE)[/math]

[math]p_{\mu} \equiv (\vec{p},iE)[/math]

Trig Method

Another way to represent the lorentz transformation is by using the substitution

[math]\sin (\alpha) \equiv \beta \equiv \frac{v}{c}[/math]

[math]\cos(\alpha) \equiv \frac{1}{\gamma} \equiv \sqrt{1 - \beta^2}[/math]

The Matrix form pf the tranformation looks like

[math]\left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )= \left [ \begin{matrix} \sec(\alpha) & -\tan(\alpha) & 0 & 0 \\ -\tan(\alpha) & \sec(\alpha) &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix} \right )[/math]

Or the reverse transformation

[math]\left ( \begin{matrix} ct \\ x \\ y \\ z \end{matrix}\right )= \left [ \begin{matrix} \sec(\alpha) & \tan(\alpha) & 0 & 0 \\ \tan(\alpha) & \sec(\alpha) &0 &0 \\ 0 &0 &1 &0 \\ 0 &0 &0 &1\end{matrix} \right ] \left ( \begin{matrix} ct^{\prime} \\ x^{\prime} \\ y^{\prime} \\ z^{\prime} \end{matrix} \right )[/math]

Notice that you just needed to change the signs for the inverse matrix [math]\Lambda^{-1}[/math]

Proper Time and Length

Proper Time

Proper Time [math]\Tau[/math]

The time measured in the rest frame of the clock. The time interval is measured at the same x,y,z coordinates because the clock chose is in a frame which is not moving (rest frame).

The time given in any frame (t) = [math]\gamma \Tau[/math]

Note

since [math]\gamma \gt 1[/math] you expect the Proper time interval to be the smallest

Proper Length

Proper Length[math] (c\Tau)[/math]

The length of an object in the object's rest frame.

Transformation Examples

Kinematics in Center of Momentum Frame

In this example we would like to determine the energy of particle #2 as seen from a referenve frame attached to particle # 1, ie; particle #1's rest frame. Our list of Lorentz invariants is

[math]\left ( p^1 \right )_{\mu} \left (p^1 \right )^{\mu}= \frac{E^2(1)}{c^2} - p^2(1) \equiv E^2 - p^2 = m^2(1)[/math]= Lorentz invariant

p_2^2 = m_2^2 : similarly

Let [math]E_{21}[/math] = Energy of particle #2 as observed by particle #1