Navigation_
⊲
△
⊳
Scattering Amplitude
In the Møller scattering (P1+P2→P′1+P′2) we have identical particles in the initial and final states. This that the amplitude to be symmetric under interchange of particles (P′1↔P′2 or P1↔P2). Due to this symmetry we can determine two 1st level Feynman diagrams to describe this scattering.
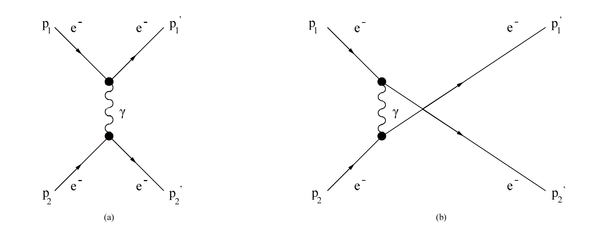
The amplitudes of the individual Feynman diagrams add linearly to form the total amplitude
M=M1+M2
Using the Feynman rules, each vertex contribute a factor
ie(pinitial+pfinal)μ
and the propagator gives
−igμνq2
where q is the momentum of the photon
q≡pfinal−pinitial
and gμν is the Mandelstam metric which allows the transformation from the contravariant to covariant form needed for tensor multiplication. Examining both Feynman diagrams seperately, we find for their individual amplitudes
−iM1=ie(p1+p′1)μ(−igμνq2)ie(p2+p′2)ν−iM2=ie(p1+p′2)μ(−igμνq2)ie(p2+p′1)ν
−iM1=ie(p1+p′1)μ(−igμν(p′2−p2)2)ie(p2+p′2)ν−iM2=ie(p1+p′2)μ(−igμν(p′1−p2)2)ie(p2+p′1)ν
−iM1=ie2((p1+p′1)μ(p2+p′2)μ(p′2−p2)2)−iM2=ie2((p1+p′2)μ(p2+p′1)μ(p′1−p2)2)
Without loss of generality, we can extend this to the center of mass frame
−iMe−e−=−ie2((p∗1+p′∗1)μ(p∗2+p′∗2)μ(p′∗2−p∗2)2−(p∗1+p′∗2)μ(p∗2+p′∗1)μ(p′∗1−p∗2)2)
Me−e−=e2(P∗1P∗2+P′∗1P′∗2+P′∗1P∗2+P∗1P′∗2(P′∗2−P∗2)2−P∗1P∗2+P′∗2P′∗1+P′∗2P∗2+P∗1P∗1(P′∗1−P∗2)2)
Using the fact that P′∗1P′∗2=P∗1P∗2P′∗1P∗1=P′∗2P∗2P∗1P′∗2=P∗2P′∗1
Me−e−=e2(2P∗1P∗2+2P′∗1P∗2(P′∗22−2P′∗2P∗2+P∗22)−2P∗1P∗2+2P∗1P′∗1(P′∗21−2P′∗1P′∗2+P′∗22))
Me−e−=e2(2P∗1P∗2+2P′∗1P∗2(P∗22−2P∗2P′∗2+P′∗22)−2P∗1P∗2+2P∗1P′∗1(P′∗22−2P′∗2P′∗1+P′∗21))
Me−e−=e2(2P∗1P∗2+2P′∗1P∗2(P∗2−P′∗2)2−2P∗1P∗2+2P∗1P′∗1(P′∗2−P′∗1)2)
Me−e−=e2((P∗21−2P∗1P′∗2+P′∗22)−(P∗21+2P∗1P∗2+P∗22)t−(P∗21−2P∗1P′∗1+P′∗21)−(P∗21+2P∗1P∗2+P∗22)u)
Me−e−=e2(u−st+t−su)
Navigation_
⊲
△
⊳
